基于自然样条补偿最小二乘的高程误差研究
2010-11-13王守春汪长余王松庆米景跃安丽丽
王守春,汪长余,王松庆,米景跃,安丽丽
(天津市水利科学研究院,天津 300061)
基于自然样条补偿最小二乘的高程误差研究
王守春,汪长余,王松庆,米景跃,安丽丽
(天津市水利科学研究院,天津 300061)
基于非参数自然样条补偿最小二乘估计方法,把 GPS高程数据与对应的水准数据的差值作为观测值,按照非参数自然样条补偿最小二乘的估计方法,得到消弱偶然误差v之后的平差值,并以此去改正 GPS高程,可以取得较好的效果。并以某河道测量采集的数据作为事例,证明该方法的有效性。
自然样条内插;补偿最小二乘;非参数;GPS高程
目前测量数据处理中,主要用到的有参数估计、半参数估计以及非参数估计。对于参数估计和半参数估计,其中参数部分的形式是需要已知的,因此它们具有较好的外延性。而对于一组不知道各参数之间关系的测量数据,参数估计的方法就显得无能为力,这恰好是非参数估计所能解决的问题。非参数自然样条补偿估计是非参数估计方法中较为常用的一种。本文基于非参数自然样条补偿最小二乘的方法来分析高程点矫正误差。
1 非参数自然样条补偿最小二乘
1.1 光滑自然样条内插
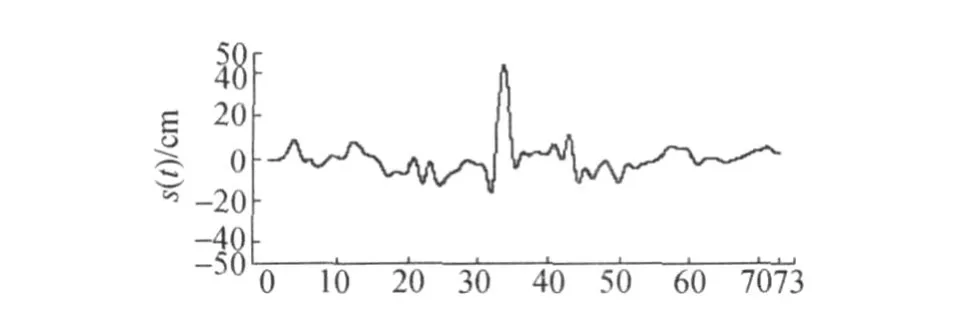
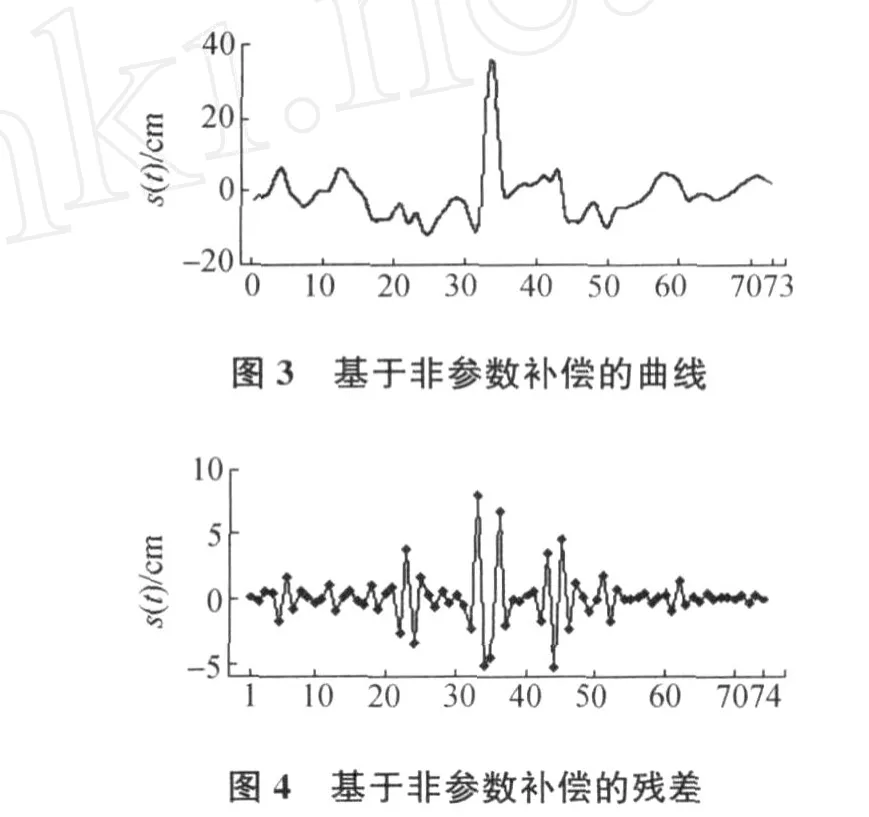
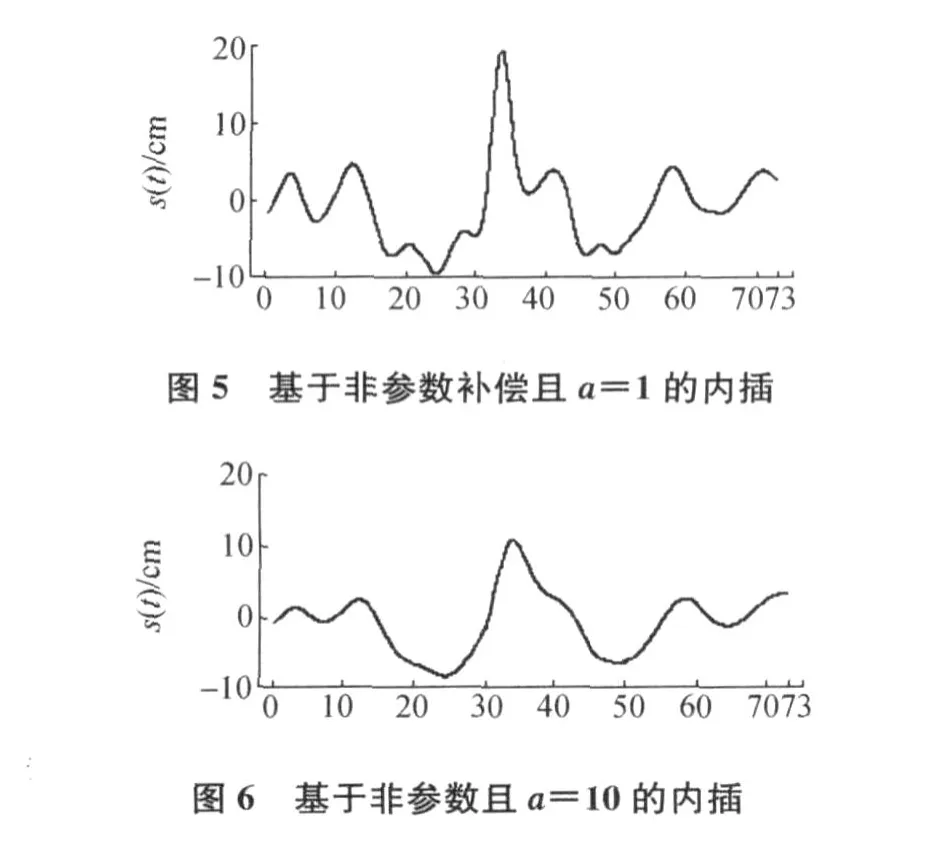
对于一组测量数据(Li,ti),i=1,…,n,希望得到一光滑曲线s(t),其内插数据点为(Li,ti),且满足s(ti)=Li,当前最为常用的方法是自然样条函数法。自然样条函数是一分段多项式函数,也即是:对某一区间[a,b]作划分,Δ:a 而对于区间[a,t1]、[tn,b],根据两对观测值[a, L0],[t1,L1]和[tn,Ln],[tn+1,Ln+1],都为线性 函数。 1.2 非参数自然样条补偿最小二乘准则 已知非参数模型 式中:s(t)是光滑曲线,Δi是白噪声,根据混杂有白噪声的观测数据Li,i=1,…,n来构造函数s(t),也成为非参数回归。如果对曲线s(t)不做任何限制而选择直线内插或样条内插,可以使得残差的平方和为0,但是这样的拟合并没有去掉或消弱噪声,所以这样的内插不是最佳的。 其中,前一项为残差平方和,后一项为补偿项。α是大于0的平滑参数,在拟合程度和光滑程度之间起平衡作用。 2.1 未加补偿项的自然样条内插 现有样本数为74的一组观测值,按区间长为1分为73个子区间,依据1.1中介绍的自然样条内插的方法对该组数据进行自然样条内插,得到的s(t)如图1所示,图2为直线内插的s(t)。 图1 自然样条内插的曲线 图2 直线内插结果 由于直线内插和自然样条内插都不能去除噪声,所以这2种内插方法对分析误差来说没有太大意义。 2.2 非参数补偿最小二乘 根据1.2中介绍的回归准则,在Matlab中进行迭代计算选取平衡参数α=0.05,s(t)及v=s(t)-L如图3、图4所示。 图4中的v也即是1.2中提到的白噪声,这样就得到了剔除白噪声后的差值s(t),并且以此去改正每公里断面上的所有高程数据,从而可以得到较为准确的高程数据。图 5、图 6分别是当α=1,α=10时所对应的s(t)。 通过自然样条补偿最小二乘的估计方法,可以对非参数(观测值)、白噪声进行估计,以此来改正各观测值,提高精度。在河道断面测量中,用该方法可以消弱由点矫正和基准转换所带来的误差。具体实施步骤如下: 1)根据已知水准点,进行三等水准测量,并在河道两岸每公里处留一个水准点; 2)用任意设站的RTK对每公里处所留的三等水准点进行测量,同时对每一个需要测量的河道断面所对应的两堤特征点(堤脚,堤顶,防浪墙等)进行测量,并用测深仪加RTK的方式测量该断面的水下高程; 3)对RTK所测量的数据进行高程点矫正,比对每公里留点处的三等水准高程与矫正过的 GPS高程,若整体差值较大,则以留点处的2种高程之差作为观测值,进行非参数自然样条补偿最小二乘估计,剔除或减弱偶然误差(白噪声),并以剔除或消弱偶然误差的观测值来改正对应断面上的所有 GPS高程; 4)生成断面成果。非参数自然样条补偿最小二乘估计方法中,确定光滑因子α仍然是一难点,还有待于进一步研究。 [1]丁士俊.测量数据的建模与半参数估计[D].武汉:武汉大学,2005. [2]柴根象,洪圣岩.半参数回归模型[M].合肥:安徽教育出版社,1995. [3]孙海燕.测量平差函数模型的若干讨论[J].武汉大学学报,2003(S):62-64. [4]丁士俊,陶本藻.自然样条半参数模型与系统误差估计[J].武汉大学学报:信息科学版,2004,29(11):964-967. [5]潘雄.半参数测量模型在 GPS高程拟合中的应用[J].武汉工业学院学报,2004,23(2):99-101. [6]胡宏昌.半参数模型的估计方法及其应用[D].武汉:武汉大学,2004. [7]丁士俊,孙振冰,刘星.广义补偿最小二乘估计及其统计性质[J].大地测量与地球动力学,2006,26(4):22-26. [8]孙海燕,吴云.半参数回归与模型精化[J].武汉大学学报:信息科学版,2002,27(2):172-174. Study on the height errors based on the penalized least square of natural spline WANG Shou-chun,WANG Chang-yu,WANG Song-qing,M IJing-yue,AN Li-li (Tianjin Hydraulic Research Institute,Tianjin 300061,China) Based in the penalized least square estimation of nonparametric natural sp line,take the difference of GPS Height and Leveling Height as observed values,and get the adjusted value w hose accidental errorvhave been reduced.Then co rrect the data of GPS Height w ith the adjusted value,thus a better result could be obtained.Finally,this theo ry is p roved effective by the data of a river surveying. natural sp line interpolation;penalized least square;non-parameter;GPS Height P224 A 1006-7949(2010)04-0027-03 2009-10-19 王守春(1984-),男,助理工程师,硕士研究生. [责任编辑:张德福]
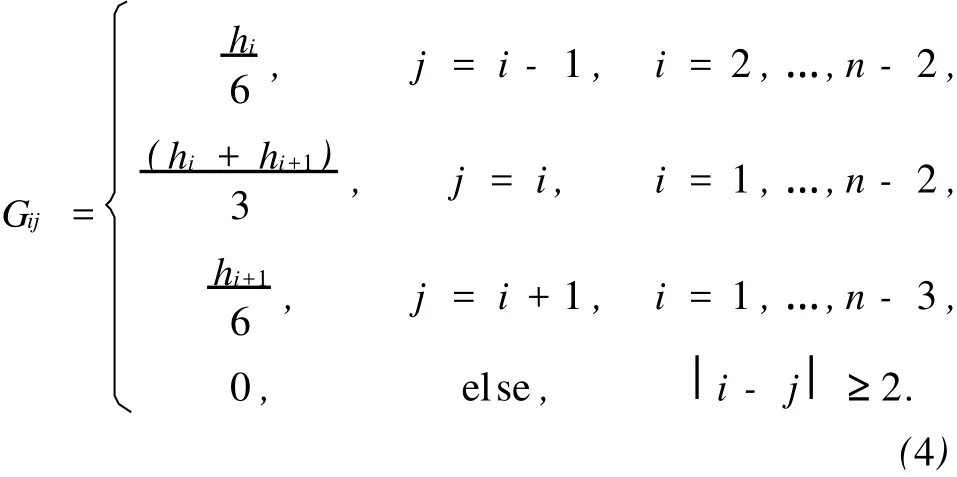
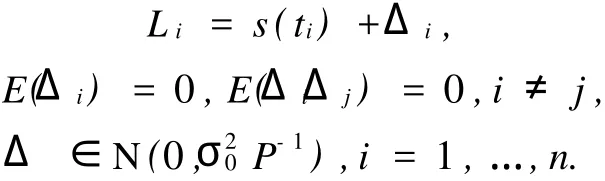
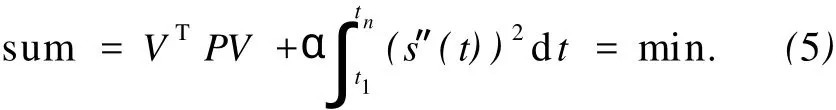
2 数据处理及结果分析

3 结 论
