基于重力场模型高程拟合残差求定GPS正常高
2010-11-13李祖锋巨天力张成增缪志选
李祖锋,巨天力,张成增,缪志选
(中国水电顾问集团西北勘测设计研究院,甘肃 兰州 730050)
基于重力场模型高程拟合残差求定GPS正常高
李祖锋,巨天力,张成增,缪志选
(中国水电顾问集团西北勘测设计研究院,甘肃 兰州 730050)
为提高GPS高程异常拟合精度并减少已知点的数量,以提高流域规划高程控制测量工作效率,文中利用重力场模型高程拟合残差建立区域较高精度的线状似大地水准面拟合模型。该方法在联测较少高等级水准的情况下,区域高程拟合精度满足流域规划控制测量对高程精度的要求。
正常高;重力场模型;高程拟合残差
利用重力场模型高程拟合残差求定高程异常的方法是:采用解析内插法,将每一个 GPS点用地球重力场模型计算的高程异常残差作为观测值,在已知高程点上求得的高程异常残差作为固定值,进行拟合处理。本文结合西汉水流域规划高程控制测量,对该方法进行阐述。
1 高程异常及其求定方法
工程领域使用的高程为测量点沿铅垂线至似大地水准面的正常高H,似大地水准面表征了地球的基本几何和物理特性,同时它又是定义正常高高程系统的基准面,是确定参考椭球形状、大小和定位的一个约束面;GPS测量得到的是相对于WGS84椭球面的大地高H84。工程中采用正常高系统,使用中要把GPS大地高转换为正常高。
大地高与正常高之间的关系见图1。
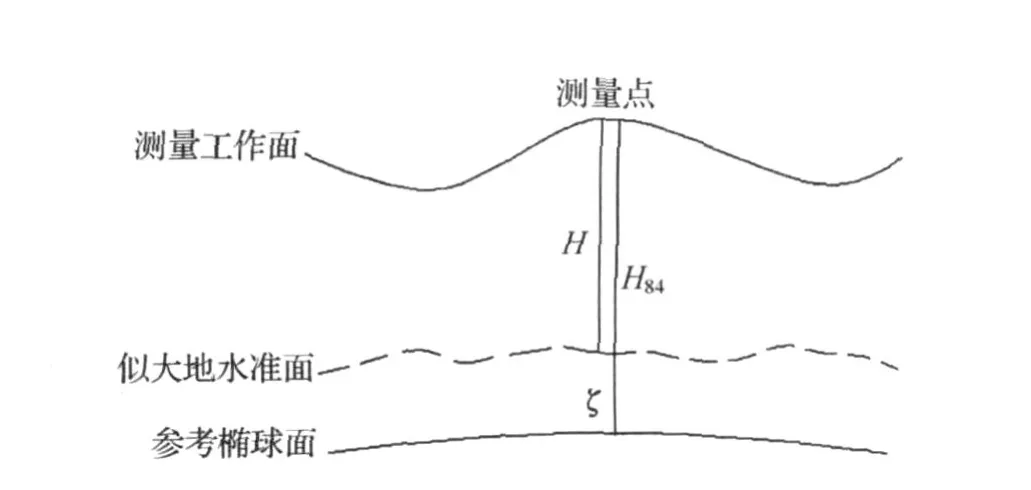
图1 大地高与正常高的关系
测量点对应的大地水准面至参考椭球面的高差ξ为该点的高程异常。已知GPS点的大地高H84和正常高H,就可以求得该点的高程异常

由式(1)可知,采用GPS定位要获得正常高H,需要知道满足一定精度要求的大地高H84和高程异常ξ,正常高的精度主要取决于大地高和高程异常的精度。大地高H84可以通过 GPS测量直接获得, GPS测定的大地高具有较高的精度,因此,GPS高程异常ξ的拟合精度成为影响 GPS高程精度的关键因素。
获取GPS测点高程异常ξ可以通过以下2种方法:
1)重力大地水准面法:可由地面重力值结合全球地球位模型和数字地形模型计算出的重力场模型资料求定待求点的高程异常ξ。目前,开放使用的是美国NASA宇航局公布的利用联合测量数据确定的EGM 96全球似大地水准面模型,其分辨率达50 km。
2)几何大地水准面法:通过联测沿测区分布的一定数量的 GPS点高程,获取这些点的高程异常ξi,通过对高程异常ξi按照一定的数学模型对区域的其余点位进行高程异常拟合,就可以求得其余点的正常高值Hi。几何大地水准面求出的高程能够同地方正高兼容,而且可将测区中的任何偏差予以平差,但几何法受到正高和GPS测量中各种误差的影响,而且可通过解析内插传播。
2 重力大地水准面高程异常求定
大地水准面相对于W GS84椭球的起伏,可由地面重力值结合全球地球位模型和数字地形模型计算得到。重力测量提供的大地水准面模型覆盖区域广,给出的地面重力值和地形数据完整、均匀,能够得出区域的或国家的大地水准面模型。全球重力场模型EGM 96是根据卫星跟踪测量数据、地面重力异常数据等确定的。根据布隆斯(H.Bruns)表示扰动位(T)与大地水准面高(N)的关系式,即

式中:γ为大地水准面上的正常重力。
得出
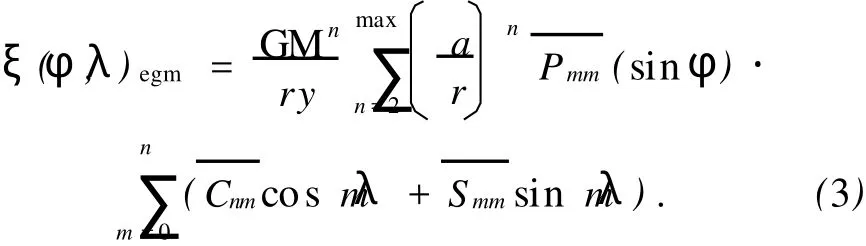
式中:GM=3.986 005×1014m3/s2为地心引力常数,a=6 378 137 m为参考椭球的长半轴,r、φ、λ分别是计算点的地心向径、维度和经度,nmax=360为完全规格化位系数,γ(φ)=978 032.68×(1+0.005 0.24×sin2φ-0.000 005 8×sin22φ) mGal为计算点的正常重力sinφ)为完全规格化Legend-re函数。由给定的EGM 96重力场模型的位系数和计算至360阶次,可得到测区任一点的高程异常ξegm。
重力场模型推算的高程异常,其绝对精度一般在±(0.5~1.0)m[1],在高山峡谷地区会更大,地方正高和重力大地水准面导出的正高之间可能存在较大的偏差,难以直接用于测量点正常高的确定。
3 利用重力场模型高程拟合残差求定正常高
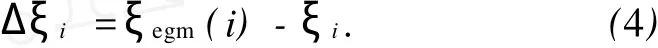
虽然重力场模型推算高程异常误差较大,但其中包含了具有一定精度的重力场中长波信息。为了对这部分信息进行有效的利用,结合几何大地水准面模型中的解析内插法,提出了利用重力场模型高程拟合残差求定正常高的方法。
设定重力场模型拟合出测点高程异常ξegm(i),沿测区范围通过高等级水准实测部分高程异常成果ξi,则测量点的重力模型高程异常拟合残差
利用拟合残差Δξ求定高程异常的方法是:采用解析内插法,将每一个GPS点用地球重力场模型计算的高程异常残差作为观测值,在已知高程点上求得的高程异常残差作为固定值,进行拟合处理。按照几何大地水准面中的线状高程异常拟合法对Δξ进行拟合,从而内插出待求点的高程异常拟合残差。
设点的高程异常残差Δξ与平面坐标x、y的关系为
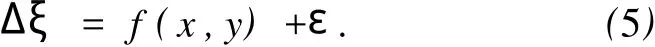
式中:f(x,y)为Δξ中趋势值,ε为误差。

对于呈线状分布的流域 GPS测量点高程异常拟合,可以采用多项式曲线拟合法,该方法是根据测线上已知点相对坐标(如累距等)和高程异常,用曲线拟合的方法,拟合出测线方向的似大地水准面曲线,再按照距离内插出待求点的高程异常,从而求出测点的正常高。
设测区 GPS各测点的Δξi与拟合坐标Si(i= 0,1,2,…,n)存在的函数关系可用式(7)的m(m≤n)次多项式进行拟合。

写成矩阵形式
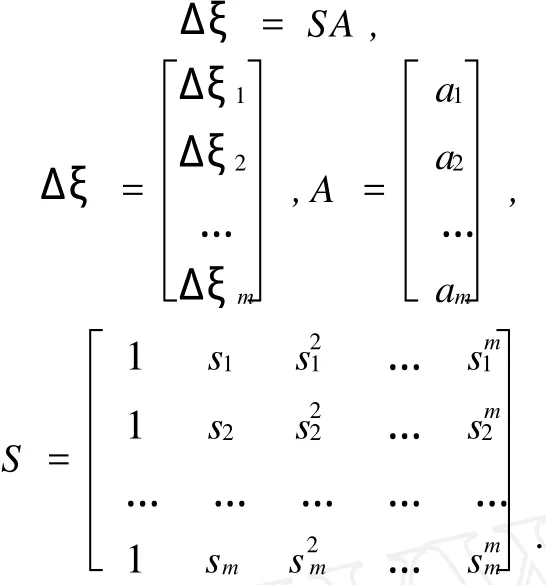
即可求出各点的Δξi(Si),将Δξi(Si)代入式(4)得出待求点的高程异常

将式(8)代入式(1)便得待求点的正常高
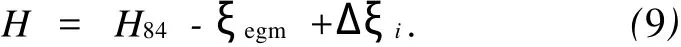
式中:H84为GPS测量大地高,ξegm为重力场模型拟合高程异常,Δξi为重力场模型高程拟合残差。
4 拟合高程精度评定
为了对西汉水流域规划 GPS高程拟合精度进行评定,在布设几何水准联测方案时,多联测若干个GPS点,其点位均匀分布在测区沿线,以做外部校核使用。
由检验点的ξi值与拟合值ξ′i,求出检验点高程拟合残差Vi=ξ′i-ξi,则GPS高程拟合计算的外附和精度为
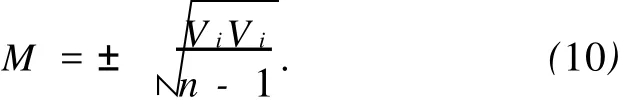
GPS拟合高程的精度评定可根据校核点至已知点的距离L,按照国家相应测量规范等级水准限差来评定GPS高程拟合所能达到的精度。
下边结合西汉水流域规划GPS测量成果,采用式(7)的多项式曲线拟合方法,利用重力模型高程拟合残差进行高程拟合。西汉水规划河道地处峡谷地带,长98 km,总落差304 m。
拟合采用6个正常高已知点,从最西边XH22开始沿控制网分布的累距为其拟合坐标S。
基于EGM 96模型拟合残差计算的5次多项式系数为
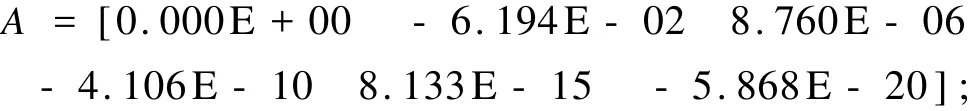
基于高程异常计算的5次多项式系数为

校核点拟合高程外附和精度见表1。
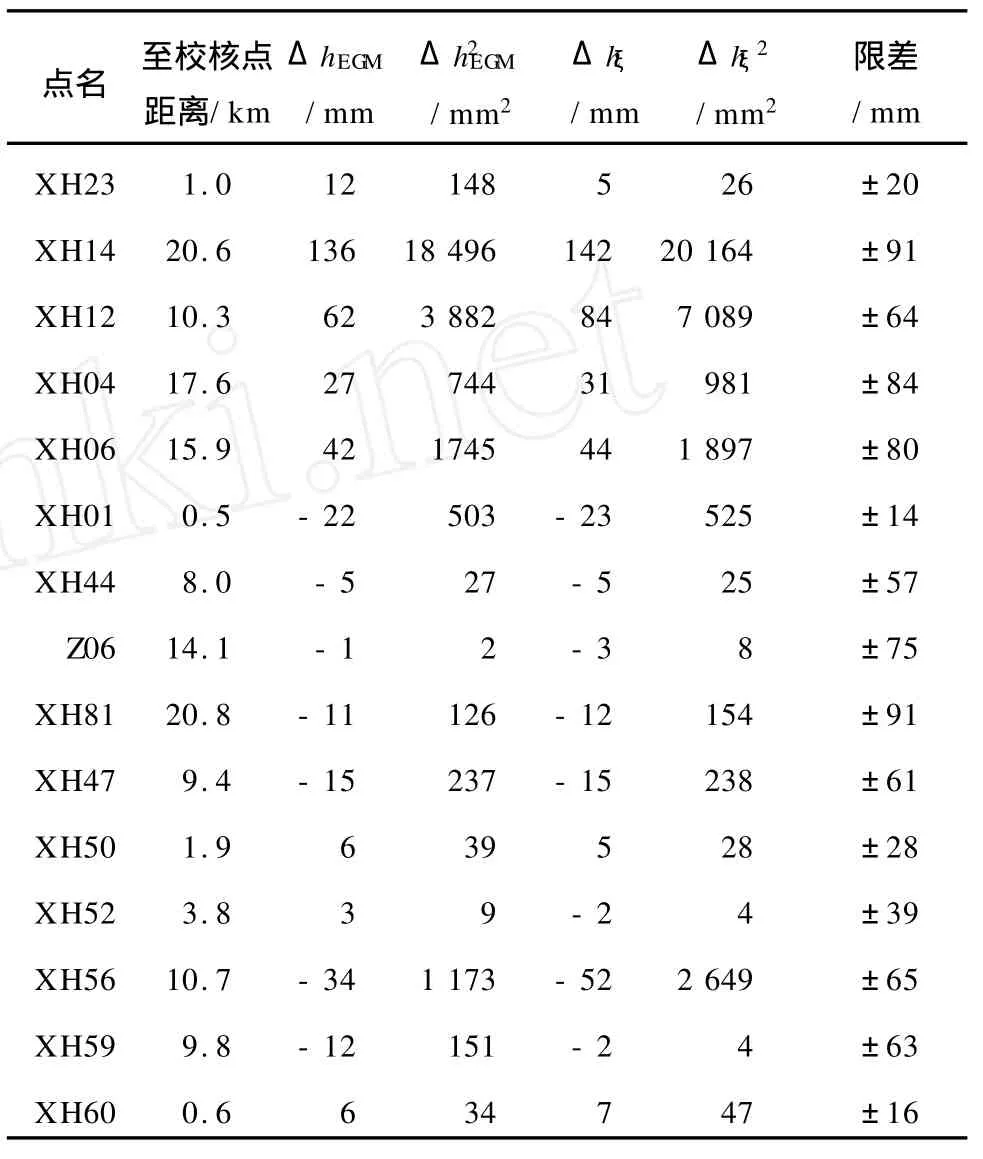
表1 GPS拟合高程外附和精度
将表1数据代入式(10),计算得 EGM 96模型拟合高程和高程异常拟合高程外附和精度分别为±44 mm和±49 mm。按照四等水准限差要求, XH14点高程超限。
表1数据显示,采用重力场模型拟合残差拟合的高程精度要优于直接采用几何高程异常拟合的高程精度。
5 结束语
GPS高程测量精度与测区条件、重力似大地水准面模型误差、已知点数量及分布、网型结构、观测方法等均有很大关系。当流域长度过大时,采用多项式曲线拟合方法建立的线状似大地水准面模型灵敏度会降低,宜对流域分段进行高程拟合。
目前,GPS拟合高程精度,对于高精度的施工等测量控制网尚达不到要求,但对于流域规划等测量工作,通过优化拟合过程,其精度可以满足规划阶段测量工作要求。
[1]叶达忠.桂中引水灌区工程三维 GPS控制网建设技术研究[J].测绘通报,2009(3):39-41.
[2]张兴福,沈云中,周全基.GPS高程异常拟合精度的估算方法[J].测绘通报,2003(8):21-22.
[3]张京礼,史振江,李瑞.GPS高程拟合精度探讨[J].测绘工程,2004,14(2):29-31.
[4]刘帅,王礼江,朱建军,等.GPS高程拟合模型的优选[J].测绘工程,2006,16(4):17-19.
[5]王增利,黄腾,邓标.基于二次曲面的拟合推估法在 GPS高程测量中的应用[J].测绘工程,2009,18(1):50-52.
[6]姚吉利,褚丽丽,于志路.GPS水准面拟合方法研究[J].测绘工程,2005,15(4):23-26.
Calculation of normal GPS height based on height fitting residual of gravity field model
(Engineering Investigation Research Institute of No rthwest Hydro Consulting Engineers,Lanzhou 730050,China)
L IZu-feng,JU Tian-li,ZHANG Cheng-zeng,M IAO Zhi-xuan
In order to further imp rove the aberrant fitting accuracy of GPS height,meanw hile to reduce the number of know n pointsand to increase themeasurement efficiency of river basin p lanning height,a regional linear quasi-geoid fitting modelw ith higher accuracy w as established using height fitting residual of gravity field model.U nder the circum stance of joint measurement w ith less high-level by this method,the regional height fitting accuracy met the height accuracy requirements of controlling measurement in river basin.
normal height;gravity field model;height fitting residual
P228
A
1006-7949(2010)04-0024-03
2009-04-13
李祖锋(1981-),男,工程师.
[责任编辑:张德福]
