Hamilton系统中Maxwell方程组的数值求解

刘双兵 陈海波 杨汉生

（巢湖学院物理与电子科学系，安徽 巢湖 238000）

Hamilton系统中Maxwell方程组的数值求解

刘双兵 陈海波 杨汉生

（巢湖学院物理与电子科学系，安徽 巢湖 238000）

在详细阐述Hamilton系统中的辛算法的基础上，给出了Maxwell方程组的Hamilton的函数形式，将辛算法保持能量守恒和辛对称性的思想应用于Maxwell方程组的数值求解，结合传统的时域有限差分（FDTD）法，得到了电磁场时间和空间的离散迭代公式，即辛时域有限差分（SFDTD）法。最后扼要地分析了该数值计算方法的稳定性及数值色散性。

哈密尔顿系统；辛算法；时域有限差分；数值色散性

1 引言

近年来，随着计算机性能的飞速发展和计算数学、计算物理中各种新型算法的出现，计算电磁学呈现出空前繁荣的局面。各种电磁场数值方法层出不穷，但这些方法面临计算时间、存储空间及计算精度等方面的困难，而且随着人们对问题的物理本质认识的深入，意识到在追求算法高精度的同时，还应力求保持原系统的内在性质。由于电磁场方程可以转化为一无穷维Hamilton系统，而Hamilton系统具有一系列的内在性质，因而在对Hamilton系统的数值求解时，保持其内在性质就显得尤为重要。辛算法正是保持Hamilton系统内在性质的一种新型数值方法，该算法在长时间的数值计算中，具有常见数值方法无可比拟的计算优势。

时域有限差分(FDTD)[1]法以其简单直观的特点已成为电磁学数值计算的一种常用方法，它直接求解依赖时间的Maxwell旋度方程，利用二阶精度的中心差分近似旋度方程中的时间及空间微分算符，极易处理非均匀媒质的情形。然而，它的计算精度相对较低，计算的时间步长与空间离散网格的大小必须满足Courant-Fredrichs-Lewy(CFL)稳定性条件，并且随着计算时间步的增加，误差将会累积。为了克服FDTD方法的这些缺点，大量文献提出了高阶FDTD方法来提高计算精度，但高阶方法对稳定性条件的要求更强；T.Namiki[2]则提出ADI-FDTD来摆脱Courant稳定性条件的束缚，但ADI-FDTD方法的数值色散性较FDTD法差。[3]总而言之，这些方法的效果并不尽如人意，原因在于这些方法破坏了Maxwell方程的辛结构。我们知道Maxwell方程可以看成一个无穷维的Hamilton系统，而Hamilton的算法应在辛几何框架内产生，该系统随时间的演化永远是辛变换演进，所以正确的离散算法应是辛变换，这样的算法称为Hamilton算法或辛算法。[4]在对Maxwell方程离散求解时，保持辛结构就显得非常重要。本文首先详细介绍了Hamilton系统中的辛算法，其次将Maxwell方程表述为Hamilton系统，在此基础上得到保持电磁场辛结构的时域有限差分方法，即辛时域有限差分（SFDTD）法，最后对其稳定性及数值色散性进行了简要分析。

2 Hamilton系统和辛算法

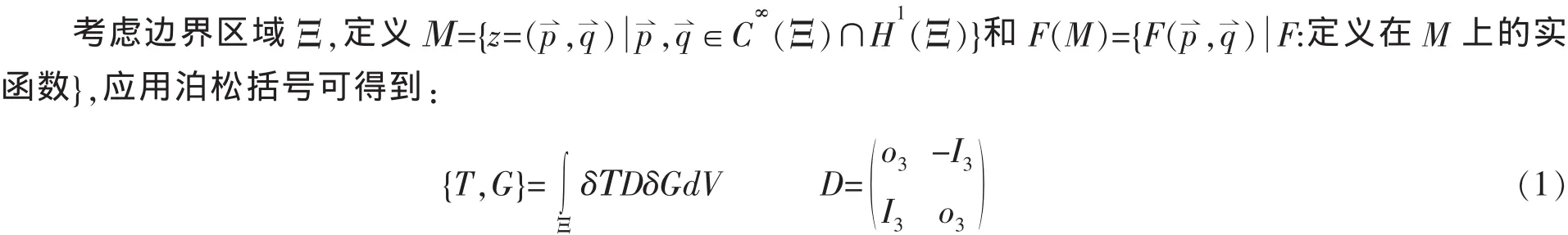
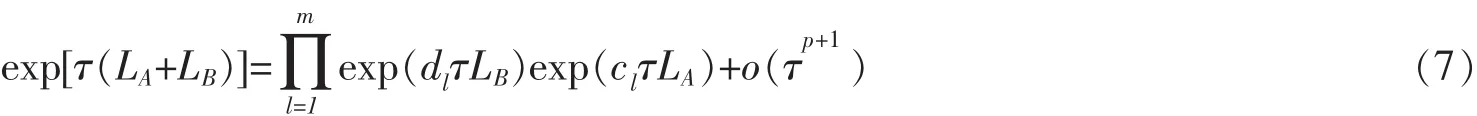
其中{cl}和{dl}是传播系数，m和p分别是辛算法的级数与阶数。该方法称之为辛传播子方法或分解算子方法。为了确定传播子系数，将（7）式在t=0点Taylor展开：

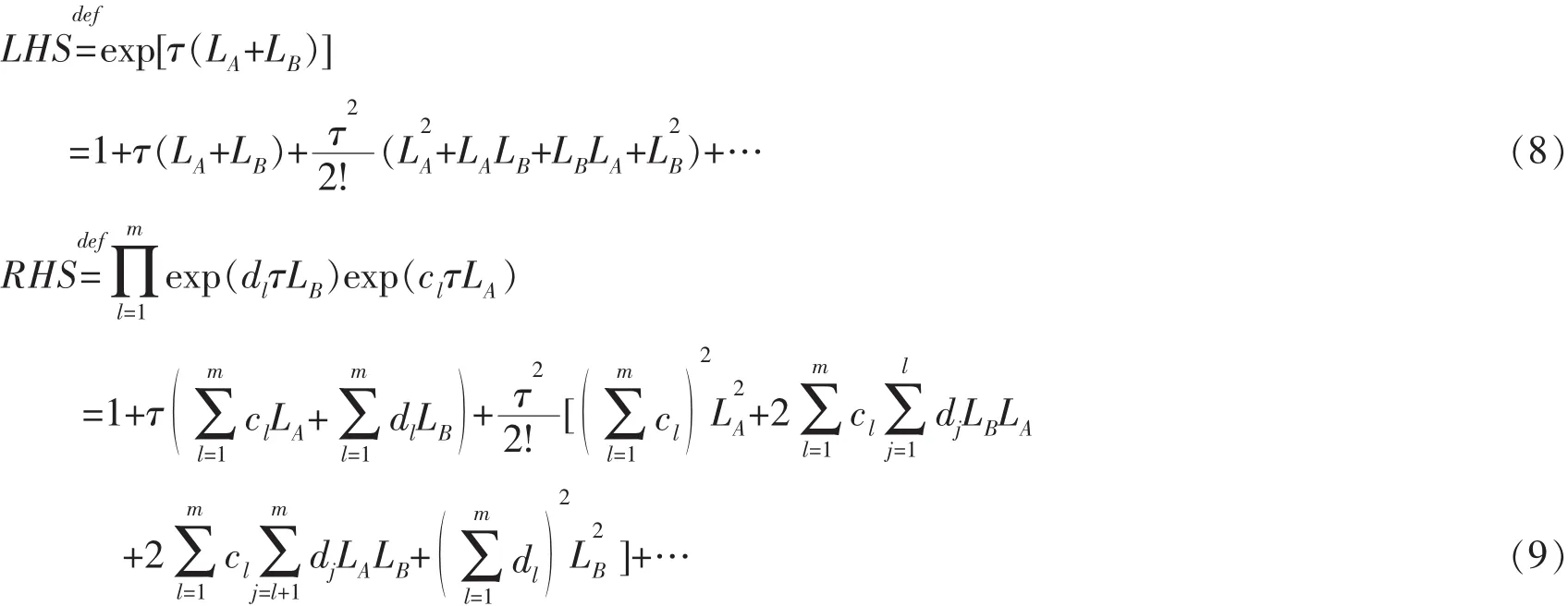
比较LHS和RHS两式中τ的多项式系数，如果直到τp为止，两端的系数都相等，则该辛算法称之为p阶辛算法，由此可确定传播子系数。常用的是二级二阶、三级三阶和五级四阶的辛算法，[7,8,9]其传播子系数如表1所示。

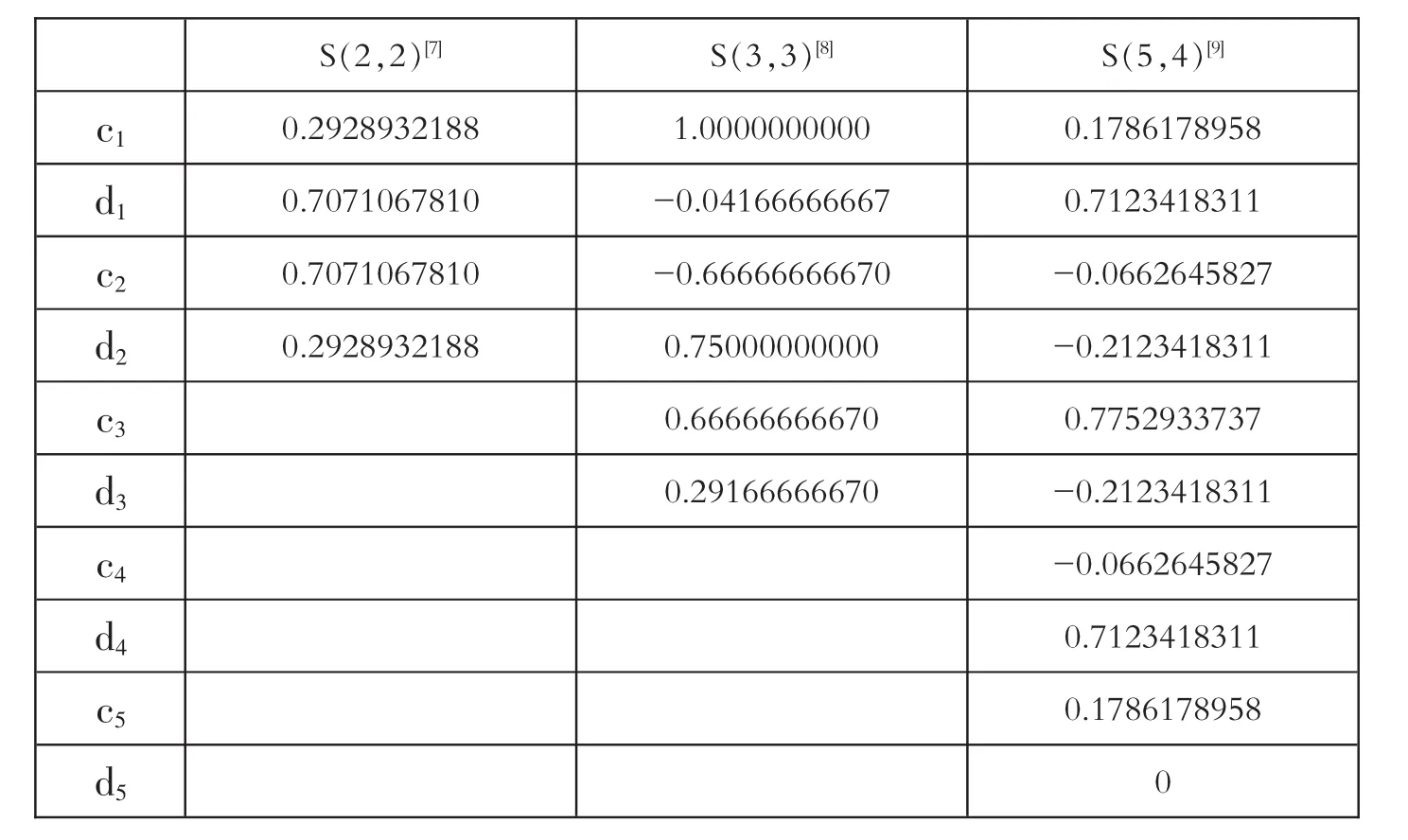
表1 m级p阶辛传播子系数

3 Maxwell方程的Hamilton表述

在线性各向同性介质中，时域Maxwell方程为：其中，ε，μ分别为相对介电常数和磁导率。

在Hamilton系统中，方程（10）和（11）可改写成无穷维Hamilton函数方程形式，即

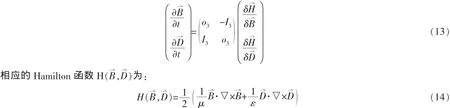
4 辛时域有限差分法（SFDTD）

由以上将Maxwell方程表述为Hamilton函数，并假设在时间尺度上，对离散网格点{nΔt，n=1，2，3…}上应用（7）式对（13）式近似计算，并根据（9）式把每个时间间隔 Δt分裂为 m 级，这样就保持了 Maxwell方程的辛性质。在空间方向上的偏微分应用离散网格点1/2，…}上的差分进行近似计算。

对（13）式，令 LA，LB分别为：

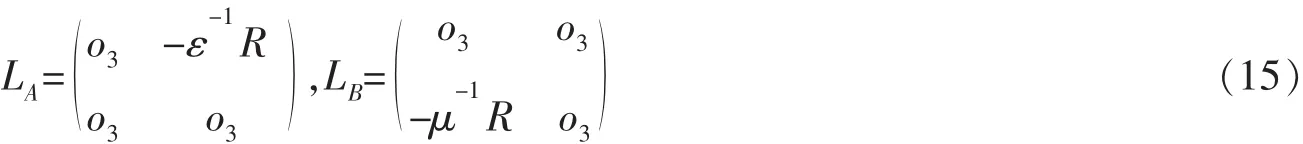
至此，辛格式有效应用于Maxwell方程组的时域计算中。

由于（LA）k=0，（LB）k=0（k=2，3…）指数函数 exp（τLA）和 exp（τLB）可以用下式进行数值计算，

对Maxwell方程组在空间方向上的离散化，将采用差分方法近似空间坐标的微分，用jΔy，kΔz；nΔt）表示 f在离散网格点（iΔx， jΔy，kΔz）上第 n 个时间步长上的函数值。 对空间采用四阶差分格式近似偏微分有：

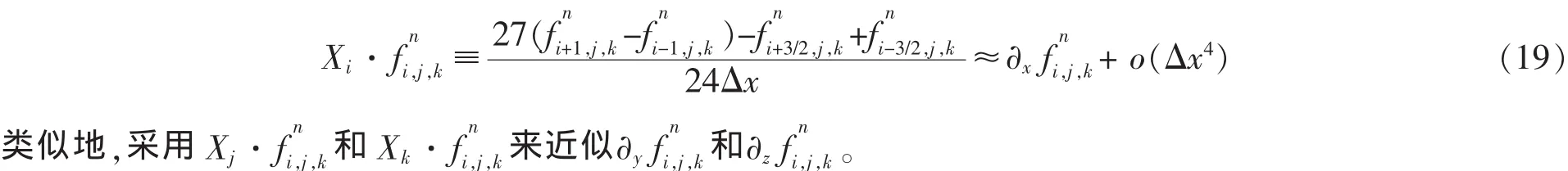
将以上m级p阶辛格式和4阶空间差分格式相结合，得到辛时域有限差分法（SFDTD），[10]记为S（m，p；4），则在x方向上的电磁感应强度Dx和Bx的迭代格式可表示为：

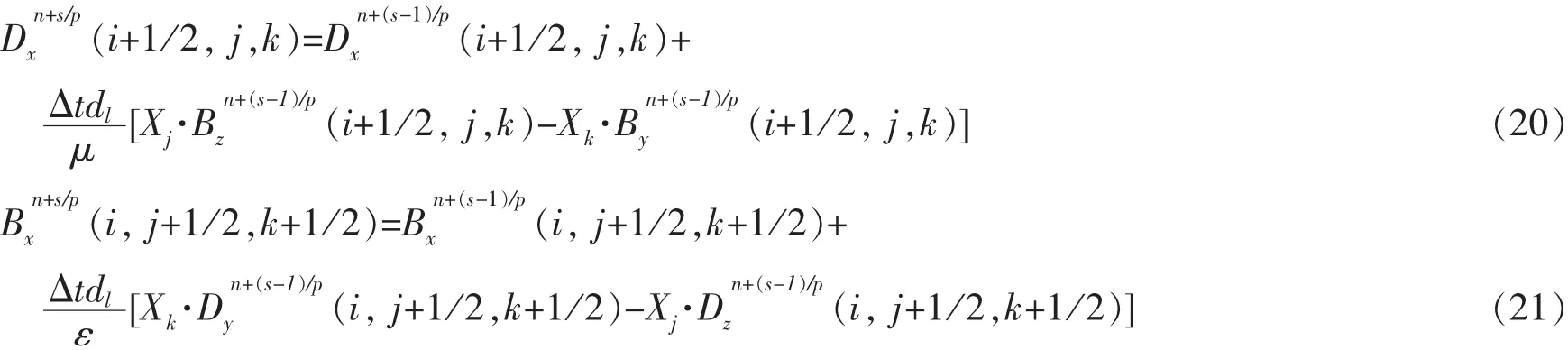
CFL的最大值即CFLmax决定了算法稳定性的上界，通过优化算法，可得到m级p阶SFDTD算法的CFLmax列于表2中，作为参考，FDTD方法的CFLmax也同时列出。

另外两个方向上的电场与磁场分量的迭代格式可类似得到。

5 SFDTD数值方法的稳定性及色散性分析

对SFDTD方法的稳定性及数值色散性的分析，可采用增长矩阵分析方法，[11]为方便分析，在以下的数值计算过程中，对空间方向上的离散采用均匀网格Δx=Δy=Δz=Δ，定义稳定性常数：

表2 SFDTD算法的CFLmax

用有限差分进行差分离散时，将会在离散网格中引起所模拟波模的色散，即在差分网格中，数值波模的传播速度将随频率而改变，这种色散将导致非物理因素引起的脉冲波形畸变、人为的各向异性及虚假的折射现象。因此，数值色散是有限差分法中必须考虑的另一个因素。

FDTD算法的数值色散关系[1]为：

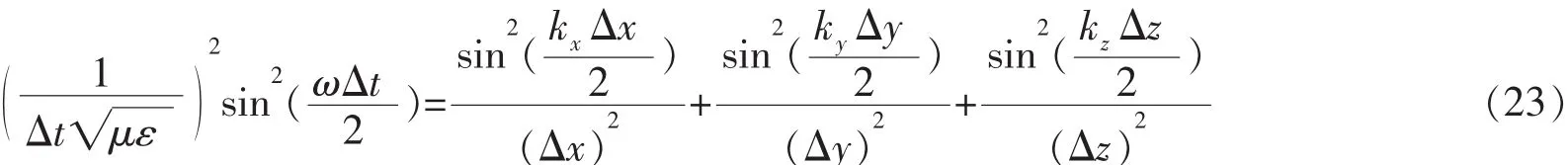
其中，为角频率 ω，kx，ky，kz为入射波矢量沿x，y，z方向的分量。

SFDTD算法的数值色散关系为：

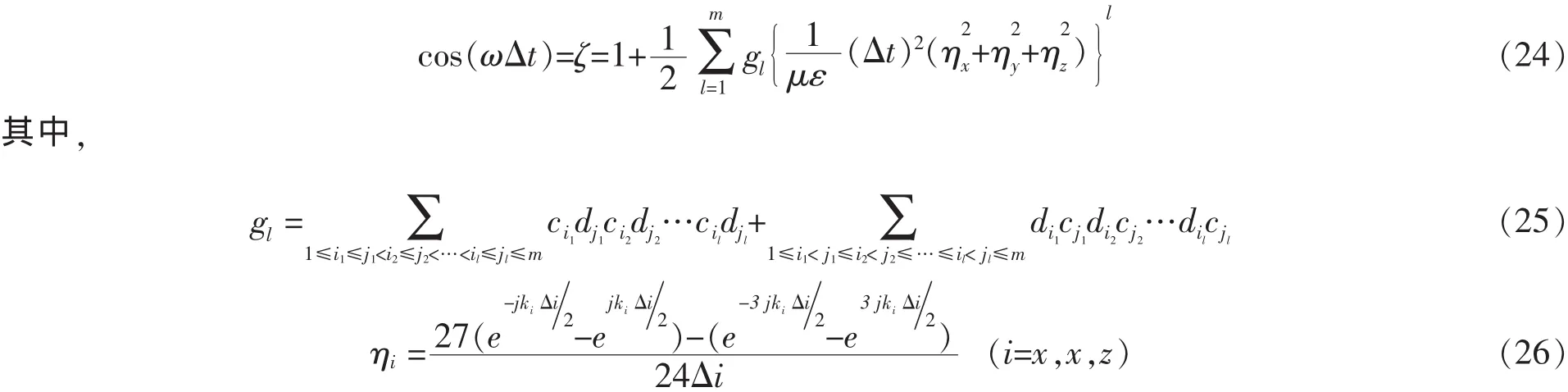
6 结论

论文重点阐述了Hamilton系统的辛传播子算法，给出了m级p阶辛算法的传播子系数，确保了该离散格式的辛结构的完整性。然后将Maxwell方程组表述为Hamilton格式，为求解该方程组开辟了新的思路，并进一步给出了Hamilton系统中Maxwell方程组的时间离散格式，结合4阶空间差分离散格式，得到了电磁场的随时间和空间推进的迭代格式，即辛时域有限差分方法（SFDTD），最后推导了该方法的稳定性条件以及由时间和空间离散引起的数值色散特性。可以说，SFDTD方法的提出，为今后进行电磁散射及辐射问题的分析计算提供了一种精确的数值方法，可行性很强。

[1]葛德彪，闫玉波.电磁波时域有限差分方法[M].西安：西安电子科技大学出版社，2001.

[2]T.Namiki.A new FDTD algorithm based on alternating-direction implicit method[J].IEEE Transactions on Microwave Theory and Techniques.1999，47:2003-2007.

[3]F.Zheng，Z.Chen.Numerical dispersion analysis of the unconditionally stable 3D ADI-FDTD method[J].IEEE Transactions on Microwave Theory and Techniques.2001，49:1006-1009.

[4]冯康，秦孟兆.哈密尔顿系统的辛几何算法[M].杭州：浙江科学技术出版社，2003.

[5]Yoshida H.Construction of higher order symplectic integrators[J].Phys Lett A.1990，150:262-268.

[6]M Kusaf，A.Y.Oztoprak，D.S.Daoud.Optimized exponential operator coefficients for symplectic FDTD method[J].IEEE Microwave and Wireless Components Letters，2005，15:86-88.

[7]Kostas T，Simos T E.Symplectic methods for the numerical solution of the radial Shrdinger equation[J].J Chem Phys，2002，34:83-93.

[8]Omelyan I P，Mryglod L M，Folk R.Optimized Forest-Ruth-and Suzuki-like algorithms for interation of motion in manybody systems[J].Comp Phys Comm，2002，146:188-202.

[9]Ruth F D，A canonical integration technique[J].IEEE Trans Nucl Sci，1983，30:2669-2671.

[10]T Hirono，W Lui，S Seki，Y Yoshikuni.A three-dimensional fourth-order finite-difference time-domain scheme using a symplectic integrator propagator[J].IEEE Trans actions on Microwave Theory and Techniques，2001，49:1640-1648.

[11]王秉中.计算电磁学[M].北京：科学出版社，2002.

THE NUMERIC SOLUTION OF THE MAXWELL'S EQUATIONS IN THE HAMILTON SYSTEM

LIU Shuang-bing CHEN Hai-bo YANG Han-sheng
（The Department of Physics and Electronics Science，Chaohu College，Chaohu Anhui 238000）

The symplectic algorithm for Hamilton function is expatiated，the Maxwell's equations are written as Hamilton function. Then the idea of keeping conversation of energy and symmetry in the symplectic algorithm is used to solve the Maxwell's equations.Combining with the traditional Finite Difference Time Domain method，we obtain the discrete iterative equations of electromagnetism in time and space domain，named Symplectic Finite Difference Time Domain algorithm.Finally the stability and the numeric dispersion of the SFDTD algorithm are analyzed simply.

Hamilton system；symplectic algorithm；finite difference time domain；numeric dispersion

O441

A

1672－2868（2010）06－0062－05

2010－09-12

巢湖学院自然科学研究资助项目（XLY-201010）

刘双兵（1982-），男，安徽宿松人。硕士研究生，助教，研究方向：电磁场数值计算。

责任编辑：宏 彬