预应力混凝土梁施工预拱度设计

伍志平

（广东省建筑设计研究院，广东广州510010）

0 前言

桥梁挠度的产生的原因有永久作用挠度和可变荷载挠度。永久作用（包括结构自重、桥面铺装和附属设备的重力、预应力、混凝土徐变和收缩作用）是恒久存在的，其产生挠度与持续时间相关，可分为短期挠度和长期挠度。永久作用挠度可以通过施工时预设的反向挠度（又称预拱度）来加以抵消，使竣工后的桥梁达到理想的线性。

预应力混凝土桥梁的预拱度通常按如下规定设置：当预加应力产生的长期反拱值大于按荷载短期效应组合计算的长期挠度时，可不设预拱度；当预加应力的长期反拱值小于按荷载短期效应组合计算的长期挠度时应设预拱度，其值应按该项荷载的挠度与预应力长期反拱值之差采用。对于位于竖曲线上的桥梁，应视竖曲线的凸起（或凹下）情况，适当增（或减）预拱度值，使竣工后的线性与竖曲线接近一致。

可变荷载挠度虽然是临时出现的，但是随着可变荷载的移动，挠度大小逐渐变化，在最不利的荷载位置下，挠度达到最大值，一旦汽车驶离桥面，挠度就告消失。因此在桥梁设计中需要验算可变荷载挠度来体现结构的刚度特性。

1 预拱度计算

1.1 构件的预拱度

预应力受弯构件的挠度由两部分叠加而成：一部分是由外荷载（永久荷载和施工荷载）产生的挠度f1，另一部分是预应力产生的反拱f2，两者的差值就是本文定义的受弯构件的挠度f，即f=f1-f2。

为了保证在外荷载和预应力作用下，梁体既不上弯也不下凹，就必须在梁体预制过程中设一个预拱度，其值与挠度f大小相等，但方向相反。

1.2 预拱度计算

（1）计算模型。以35 m中跨T梁梁体在预制、吊运、存放阶段的拱度变化作为研究对象，梁体承受预应力和自重作用。假定梁体为等截面（见图1），梁的已知条件如下：梁体全截面共配钢铰线30束，分3个孔道，上中下3个孔道钢铰线的束数分加为9、9、12，钢铰线直径Φj=15.24 mm，公称截面积140 mm2,弹性模量Ep=1.95×1011Pa，标准强度fpk=1 860 MPa，控制应力 δcon=0.75fpk=1 395 MPa,混凝土强度等级为C50，弹性模量Ec=3.45×1010Pa，张拉时混凝土的立方体抗压强度标准值fcu=40 MPa，梁体自重q=20.7 kN/m,计算跨度l=34.22 m。

（2）截面几何特征。经计算，跨中截面几何特性如下：钢铰线重心至截面下边缘的距离y1=0.21m；换算截面重心至截面下边缘的距离y0=1.256 m；换算截面惯性矩I0=0.494 27 m4；净截面重心至截面下边缘的距离yn=1.296 m；净截面惯性矩In=0.463 33 m4。

（3）由自重产生的挠度f1。跨中截面挠度f1可按一般材料力学的公式计算，即：

式（1）中：M——梁重作用下的跨中弯矩；

B0——全截面的抗弯刚度，B0=0.95EcI0，0.95为刚度折减系数。

将有关数值代入，求得f1=3.07 cm。

（4）由预应力产生的反拱f2。梁体施加预应力后，预应力在梁体中产生偏心预压力，梁体产生反拱f2。在本例中，梁体内钢束的布置为两段直线夹一段半径为5 000 m的圆曲线，钢束布置可近似为图2所示的三段直线。

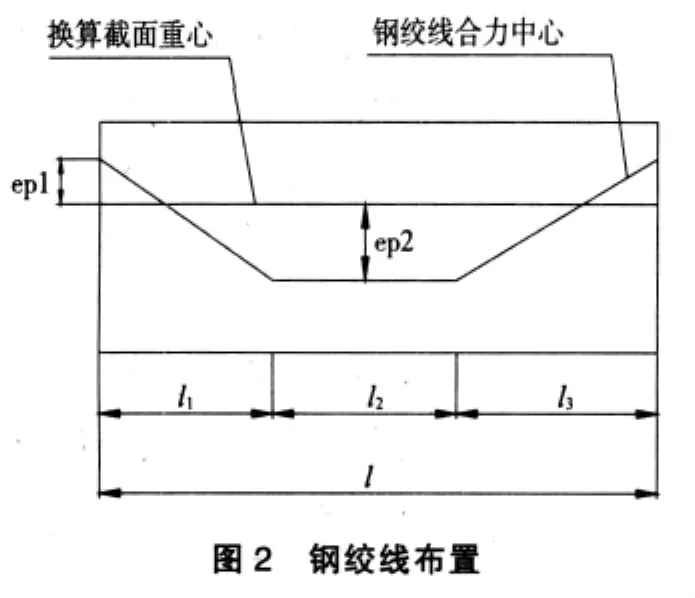
根据结构力学公式，跨中截面反拱为：

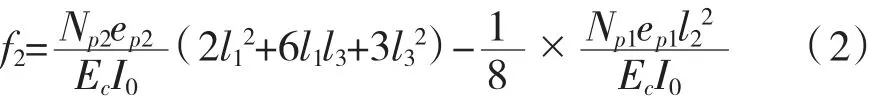
式（2）中:Np2——扣除预应力损失后预应力钢筋在跨中截面的总拉力；

现场设备层主要是计量器具，包括远传智能水表、三相智能远传电表、多功能电表等，可采集实时用水量，实时用电量、实时电压、实时电流、实时有功功率、实时无功功率、实时功率因数、实时频率等参数[3]。

ep2——跨中截面构件合力点至净截面重心轴的偏心矩，在本例中ep2=1.086 m；

Np1——扣除预应力损失后预应力筋在端截面的总拉力；

ep1——端截面构件合力点至净截面重心轴的偏心矩，在本例中ep1=0.054 m；

l1、l2、l3、l——各段钢铰线的长度，在本例中分别为 8.09 m、17.11 m、9.02 m、34.22 m。

梁体施加预应力后，混凝土的徐变变形会使梁的反拱值增大，因此，用结构力学方法按刚度EcI0计算预应力混凝土预加应力引起的反拱值时，应乘以长期增长系数。计算使用阶段预加应力反拱值时，预应力钢筋的预加应力应扣除全部预应力损失，长期增长系数取用2.0。

扣除相应的应力损失后，端截面的总拉力Np1=5.47×106kN，而跨中截面的总拉力Np2=4.68×106kN。

将以上各相关数值代入计算公式，求得f2=7.57cm。

（5）总挠度：f=f1-f2=3.07-7.57=-4.50 cm。这就是需要设置的跨中处的反拱值。

2 预拱度的设置及效果

2.1 预制梁台座顶面处置

设置预拱度的方法，是将预制梁台座顶面作成下凹曲面。如果曲线设置得当，则梁体在自重和预应力作用下经过一段时间的变形，梁体将既不上拱也不下凹。

考虑到每个台座的循环次数较多，施加预应力后台座两端受力下压，有部分变形不易恢复，故采取在施工中将台座中央下凹5.40 cm，下挠曲线形式为二次抛物线，抛物线方程为y=0.017 5x2-5.40（式中x单位为m，y单位为cm），台座形式如图3。

2.2 预拱度观测

由于设计的梁型较多，而实际施工中各种梁型都是按一种预拱度进行控制的，为了使观测结果更具有代表性，我们选取了跨径和截面型式相同的2片铁路桥梁、4片公路桥梁共6片梁进行观测。观测时间分别为存梁的第1、第10、第30、第60、第90、第120、第180天共7个时间点进行观测，观测数据如表1。

表1 各个观测时间点下主梁跨中上挠值

2.3 数据分析

2.3.1 观测数据的特点

可以看出，梁体挠度值的变化有以下特点：

（1）经过80 d的存梁期后，梁体的挠曲变形仍未停止，部分变形将在使用阶段完成。

（2）梁体上挠值随时间增加而减小，但上挠值的变化与时间并不成线性关系。在施加预应力初期，上挠值的变化较快，随梁体混凝土龄期的延长，上挠值的变化越来越慢。

（3）铁路桥梁的上挠值的变化要比同条件下公路桥梁的上挠值要大。一般情况下，在梁体施加完预应力后，铁路桥梁的上挠值要减少2.5 cm左右，而公路桥梁的上挠值要减少1.5 cm左右，在经过相同的存梁期后，铁路桥梁的剩余上挠值要小于跨公路桥梁。

（4）同为铁路桥梁或同为公路桥梁，施加完预应力后梁体的预拱度值经过相同存梁时间后剩余的预拱度值亦不相同。

2.3.2 原因分析

（1）图3中，梁体预拱度变化除与梁体自重、施加预应力大小有关外，还与混凝土的收缩徐变有关，而后者又与张拉时梁体的混凝土强度、养护和加载龄期以及使用过程中外部环境条件等有关。施加预应力大小是跨铁路梁与跨公路梁预拱度变化相差较大的主要原因，因为这两种梁自重相差很小，但钢绞线的配置却相差较大，跨铁路梁要比跨公路梁多配置3～5根钢绞线，控制张拉力相差585.9～976.5 kN。

（2）不同的台座或同一台座预制不同的梁时，其下挠曲线与设计的并不完全相同，这是造成同一种梁型，施加相同的预应力后，经过相同的时间剩余的预拱度各不相同的主要原因。

在今后的施工中，应针对不同的梁型设置不同的预拱度值，使预拱度的设置进一步趋于合理。

[1]向中富.桥梁施工控制技术[M].北京:人民交通出版社，2001.

[2]雷俊卿.桥梁悬臂施工与设计[M].北京:人民交通出版社，2000.

[3]JTG D62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[4]JTG D60-2004，公路桥涵设计通用规范[S].