卷弧尾翼火箭弹侧向气动特性数值计算
2010-11-08谢志敏杨树兴
谢志敏 ,杨树兴 ,陈 伟
(北京理工大学宇航科学技术学院,北京100081)
0 引 言
卷弧翼是为筒式发射设计的一种翼型,自50年代中期问世以来,已被广泛应用于多种战术武器,例如多管火箭、反坦克导弹、末制导炮弹、航空炸弹、巡航导弹等[1]。但是由于卷弧尾翼的不对称性,卷弧尾翼火箭弹即使在零攻角零安装角时也会产生自诱导滚转力矩,而在有攻角飞行时会产生垂直于攻角平面的侧向力和侧向力矩[2]。目前对卷弧翼的研究主要集中在卷弧翼和平直翼的差别[3]及利用试验方法研究卷弧翼的自诱导滚转特性[4],对卷弧翼的数值模拟主要是为了进行定性的流场分析或为实验设计提供依据[5,6],针对卷弧翼侧向力的数值研究很少,而侧向力和侧向力矩对卷弧翼飞行器的动稳定性有着重要的影响,且不易通过试验方法获得。在计算机技术快速发展的今天,对流场的数值模拟不仅可以大大减少研究费用,还能提供很多风洞实验无法提供的气动参数,再现流场各个位置的流场变量分布,便于对气动特性的分析。因此本文主要采用计算流体力学(CFD)方法来对卷弧尾翼火箭弹侧向气动特性进行研究。
1 数值模拟方法
1.1 流场设置
为了检验数值模拟的精度,对具有风洞实验数据的模型进行模拟,获得的气动力系数与实验数据对比。在模拟该模型时,综合考虑计算精度、计算时间、计算所需内存,采用显式算法耦合求解三维N-S方程,湍流模型采用Spalart-Allmaras方程湍流模式。本文模拟了4马赫下该火箭弹模型的流场,设定压力远场的边界条件为压强101325Pa,温度为288K,设定火箭壁面为无滑移壁面,根据需要设定速度大小和方向,以压力远场的边界条件为初始条件对流场进行初始化。图1为流场网格示意图。
1.2 气动力/力矩系数与实验数据对比
图2给出了4马赫下升力系数,俯仰力矩系数,阻力系数数值计算值和实验值,两者吻合很好,计算结果令人满意,表明文中采用的计算方法和网格划分可以准确地模拟卷弧尾翼火箭弹流场。
2 侧向力研究与分析
2.1 侧向力机理研究
在分析侧向力机理时,模拟展长120mm,弦长80mm的矩形卷弧尾翼火箭弹在4马赫10°攻角下的绕流流场,其中模型全长1520mm,弹径60mm,卷弧尾翼安装角0°。模型的安装角设为0°是为了排除尾翼斜置的影响,单独研究卷弧尾翼和有攻角来流的互相作用。

图1 火箭弹纵向切面网格图Fig.1 Mesh of rocket model

图2 4马赫下气动系数对比图Fig.2 Curves of aerodynamic coef ficients at Mach 4
计算结果显示,从前缘往后缘,流场受翼片干扰沿着弹体轴向逐渐加大,高压区面积在后缘达到最大。弹体右边的两片翼和左边的一片翼其迎风面压强都大于背风面压强。弹体下部的翼片凹凸面压力分布也存在差异,而且弹体下部翼片由于处于迎风一侧压强较弹体上部翼片压强大。因此可以确定,弹体两侧压力分布出现不均衡,将产生垂直于攻角平面的侧向力。
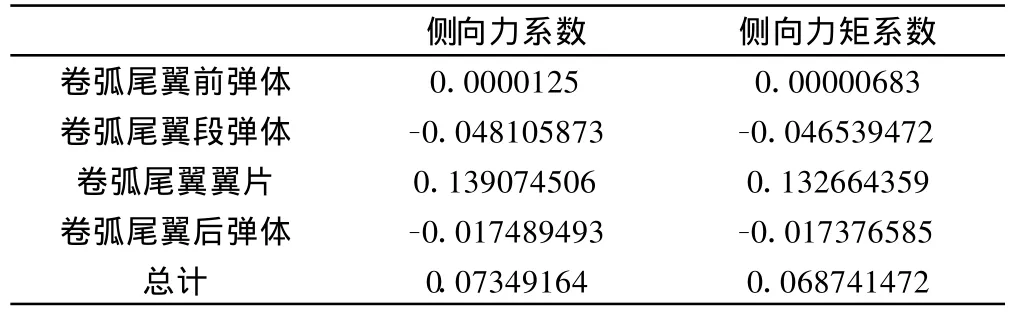
表1 全弹各部侧向气动系数表Table1 Side force and moment coefficients of all components
表1给出了数值计算得出的全弹各部分的侧向力和侧向力矩系数。不难看出,卷弧尾翼火箭弹侧向力由卷弧尾翼翼片,卷弧尾翼段弹体,卷弧尾翼后弹体和卷弧尾翼前弹体产生。而其中卷弧尾翼前弹体产生的侧向力可以忽略,卷弧尾翼翼片对侧向力产生起主要作用,弹身产生的侧向力与翼片产生的侧向力方向相反。
2.2 展弦比对侧向力的影响
无论弹身还是弹翼产生的侧向力,都是因为流场受到了卷弧尾翼扰动产生不对称压力分布所致。因此影响这种扰动的翼展、弦长、翼片曲率半径和滚转角的变化都将改变侧向力和侧向力矩的大小。在分析展长、弦长对侧向力的影响时,保持卷弧尾翼径向投影面积不变,这主要是为了保持法向力及其力矩的不变,从而不改变全弹纵向气动特性和纵向稳定性。图3为不同展弦比的三组翼形示意图及侧向力系数随展弦比变化图,由上到下依次为展长102.2mm,展弦比0.905;展长120mm,展弦比1.333;展长137.28mm,展弦比2.229。
由图3可以看出,侧向力系数随攻角、马赫数和展弦比变化发生一定的改变。虽然改变的数值较小,为10-2量级,但是由于侧向力系数本身较小,其相对变化非常大。而且侧向力系数随着攻角增大值也在不断增大,在4°到6°攻角时变化较其他攻角时更快。展弦比为0.905和1.333的两种模型的计算结果显示马赫数增大,侧向力系数增大,而展弦比2.229的模型结果与此相反。同一马赫数下,随着展长和展弦比的增大,侧向力系数明显增大,由此可以看出,在卷弧尾翼投影面积不变时,侧向力系数与展长的变化一致。
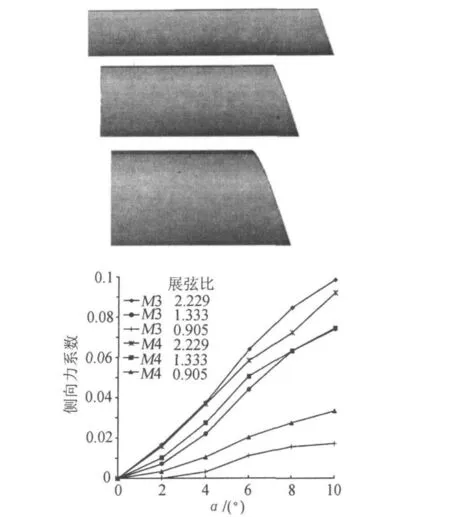
图3 三组不同展弦比翼形图及侧向力系数变化图Fig.3 Sketch of three fins with different span to chord ratiosand curves of sideforcecoefficients at Mach 3 and 4
2.3 翼曲率半径对侧向力的影响
分别研究卷弧尾翼曲率半径为20mm,30mm和40mm时全弹的侧向力,同样保持卷弧尾翼投影面积一致。图4为不同曲率半径的三组翼形的示意图及侧向力系数变化图。不难看出,侧向力系数受卷弧尾翼曲率半径变化产生的差异较小,同一马赫数下随曲率半径的增大侧向力系数减小。在4°到6°攻角时,侧向力系数随攻角的变化率较其他攻角时大。
2.4 滚转角对侧向力的影响

图4 三组不同曲率半径翼形图及马赫数3、4下侧向力系数随曲率半径变化图Fig.4 Sketch of three fins with different radii and curves of sidef orcecoefficients at Mach 3 and 4
本文模拟的火箭弹模型的六片卷弧尾翼沿弹体周向均匀分布,两片翼片之间为六分之一弹体周长。因此只要翼片绕弹体纵轴旋转一个小于60°的角度,相对于弹体纵向对称面,卷弧尾翼的分布都将发生改变。卷弧尾翼分布的变化必将改变卷弧尾翼各翼片的压力分布,进而改变全弹的侧向力系数。图5给出了滚转角分别取 0°,15°,30°,45°,60°的卷弧尾翼翼片分布,图6则为侧向力系数随滚转角变化图。
从图6可以看出,随滚转角的增大,侧向力系数先减小再增大。由于本文研究的模型是六片卷弧尾翼火箭弹,因此滚转角范围在0°到60°。在所取的5个角度中,全弹侧向力系数于0°和60°时达到最大值,于30°时达到最小值。此外卷弧尾翼火箭弹一般都有滚转角速度,达十多转每秒,因此侧向力将以60°为周期,呈周期性变化。
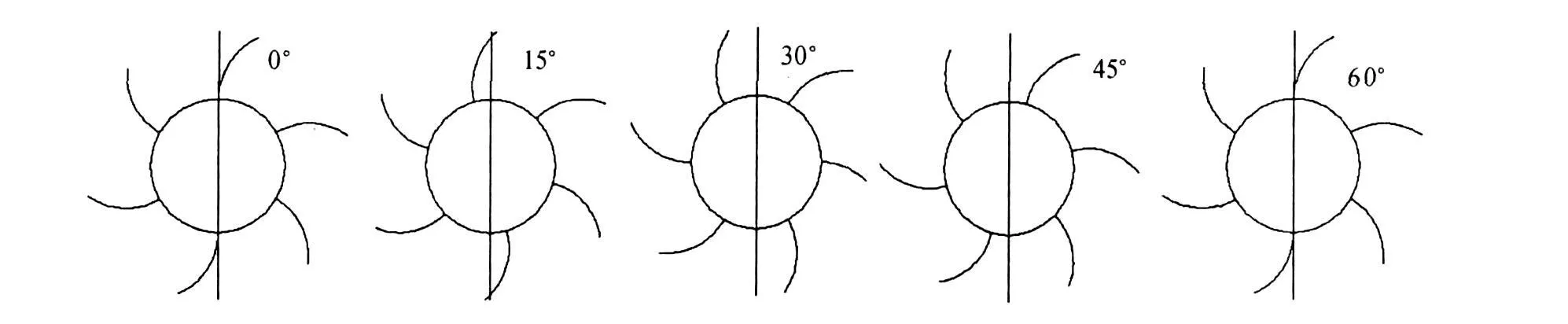
图5 不同滚转角示意图Fig.5 Sketch of different rolling angles orientation

图6 不同滚转角时全弹侧向力系数变化图Fig.6 Curves of side force coefficients under different rolling angles orientation
综上,卷弧尾翼沿弹体周向的排布对侧向力存在很大的影响。因此合理选择卷弧尾翼滚转角速度对减小全弹侧向力十分重要。
3 结 论
(1)卷弧尾翼特定外形对火箭弹流场产生了不对称扰动,导致卷弧尾翼翼片和弹身压力
分布出现不均,进而产生了侧向力,翼片产生的侧向力为全弹侧向力的主要部分,弹体其他部位产生的侧向力与之方向相反。
(2)超声速时同一马赫数下,若卷弧尾翼投影面积一定时,侧向力系数随展长减小而减小,因此为了减小侧向力,可以通过减小展长,增大弦长的方式来实现。
(3)超声速时同一马赫数下,若卷弧尾翼投影面积一定时,侧向力系数随翼曲率半径增大而减小,但是曲率半径对侧向力影响权重较小,因此不宜通过改变曲率半径来减小侧向力。
(4)不同滚转角时,侧向力系数变化很大,且呈周期性变化。弹体滚转时,侧向力变化频率与翼片之间的夹角有关,进而与翼的片数关联。
(5)侧向力矩变化趋势跟侧向力一致。
[1]吴甲生,居贤铭,苗瑞生.卷弧翼气动特性研究进展[J].力学进展,1995,25(1):102-113.
[2]毛雪瑞.卷弧翼火箭圆锥运动研究[D].[硕士学位论文].北京:北京理工大学,2006.
[3]雷娟棉,居贤铭,苗瑞生.多片尾翼布局弹箭气动特性数值计算[J].北京理工大学学报,2003,23(6):686-689.
[4]CARL P,TILM ANN.Characterization of the flowfield near awrap-around fin at supersonic speeds[R].AFRLVA-WP-TR-1998-3058.
[5]鞠玉涛.弧形翼-身组合体空气动力特性的数值模拟研究[D].[博士学位论文].南京:南京理工大学,1999.
[6]宋旭民,夏刚,秦子增,寇保华.弧形翼弹零攻角流场数值模拟[J].战术导弹技术,2002,(6):21-24.
