30P-30N多段翼型复杂流场数值模拟技术研究

王运涛,王光学,张玉伦

(1.空气动力学国家重点实验室,四川绵阳 621000；2.中国空气动力研究与发展中心,四川绵阳 621000)

0 引 言

随着计算机硬件技术和CFD技术本身的发展,采用基于雷诺平均NS方程(RANS)的数值模拟软件已经可以模拟真实飞行器的复杂外形及全机的复杂流场,包括二维高升力翼型和三维带增升装置的全机构型[1]。基于RANS方程预测巡航构型气动特性变化趋势和模拟全湍流附着流动的能力已经逐步得到飞行器设计工程师的认可,但高升力构型的数值模拟可信度水平依然很低。采用CFD手段尚很难准确模拟高升力构型的最大升力系数及失速攻角,特别是对于存在明显分离区的复杂流动,准确预测分离流动的开始和发展,以及雷诺数效应依然是CFD的难点之一。

为了研究高升力构型的流动机理,提高CFD软件的数值模拟精度,空气动力学的试验工作者和CFD工作者付出了巨大的努力[2-4],高升力构型的数值模拟也是许多CFD可信度专题会议的主题。高升力构型的主要模拟难点在于:边界层转捩、激波/边界层干扰、粘性尾迹区干扰、尾迹与边界层掺混和分离流动等等。尽管采用RANS方程模拟高升力构型存在诸多困难,尤其是工程湍流模型的适用范围众说纷纭,但采用RANS方程和工程湍流模型依然是模拟飞行器复杂构型的主要手段。Rumsey等人[5]对多位国外研究者的工作进行了综述,研究表明,考虑气动弹性影响和转捩位置有助于提高多段翼型的数值模拟精度。随着网格生成技术、大规模并行计算技术和工程湍流模型研究工作的不断深入,采用RANS方程模拟高升力构型的可信度水平有望达到一个新的高度。计算结果与试验结果进行对比不应该局限于升力、阻力等总体气动特性,还应该包含压力分布和粘性剪切层数据的精细比较。

本文通过求解任意坐标系下的雷诺平均的N-S方程,采用多块对接结构网格技术,在与相应试验结果对比的基础上,详细研究了SA一方程湍流模型、SST两方程湍流模型、不同的转捩位置对该翼型压力分布和典型站位速度型的影响。本文的研究结果表明,采用全湍流模拟方式可以较好地模拟该多段翼型的压力分布,但对速度型的模拟精度较差；模拟试验的转捩位置可以改善主翼附面层与前缘缝翼边界层发展的模拟精度；采用微吸气技术推迟前缘缝翼的转捩位置,可以进一步提高主翼上缝翼尾迹区的数值模拟精度。

1 计算构型和计算方法

麦道航空公司的30P-30N三段增升构型是被CFD工作者广泛采用的多段构型之一,该翼型的前缘缝翼和后缘襟翼的偏角均为30°,前缘缝翼的缝道宽度为2.95%,外伸量为-2.5%；后缘襟翼缝道宽度1.27%,外伸量为0.25%,是典型的着陆构型。30P-30N三段翼型曾作为1993年NASA Langley举行的CFD Challenge Workshop算例,其风洞试验主要是90年代在NASA Langley的低湍流度增压风洞中完成的,主要包括测压试验和边界层测量等,试验雷诺数5×106～16×106。试验中采用了侧壁吸气方法来保证近似的二维流动特性,但试验结果表明,攻角大于16°后,流动的三维效应较强,这会对试验与计算结果的比较产生一定的影响。计算构型、速度型测量位置如图1所示。本文模拟的状态为:马赫数M=0.2,攻角 α=19°,雷诺数Re=9×106。该攻角已接近失速攻角,这使得该状态的流动模拟更具挑战性。

本文的数值模拟采用了多块对接结构网格技术,“C”型网格为主导,计算区域的远场边界取为120倍弦长。壁面的第一排网格达到了1.0×10-6弦长,网格在各个剪切层附近均进行了适当的加密,以保证附面层内和剪切层的数值模拟精度,网格规模达到了16万。图2给出了计算网格的局部放大图。

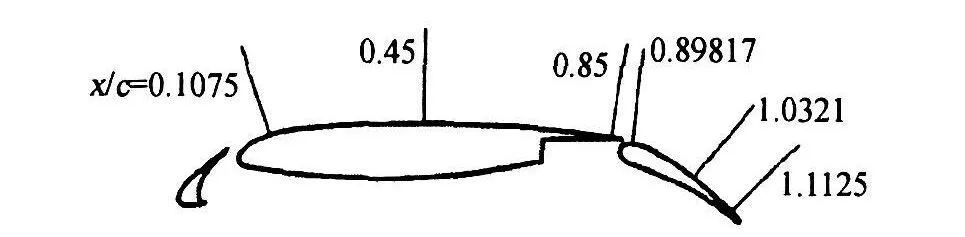
图1 30P-30N构型及速度型站位Fig.1 30P-30N profile locations

图2 30P-30N的计算网格(局部放大)Fig.2 30P-30N computational grid(local)

本文的数值模拟软件采用了中国空气动力研究与发展中心自行研发的CFD软件TRIP2.0(TRIsonic Platform Version2.0)。该软件采用结构网格技术和有限体积方法,通过数值求解三维任意坐标系下的Reynolds-Averaged Navier-Stokes(RANS)方程 ,获得绕流复杂飞行器的绕流流场。在本文的数值模拟中,离散方程组的求解采用LU-SGS方法,无粘通量的离散选择了三阶精度的ROE格式,粘性通量的离散采用中心格式,湍流模型采用了SA一方程和SST两方程模型,计算中采用了多重网格技术加速收敛。

2 全湍流模拟结果与分析

图3给出了采用SA一方程模型和SST两方程湍流模型壁面压力分布的计算结果,同时给出了相应的试验结果。没有考虑试验的转捩位置,湍流模型方程全流场求解。必须指出的是,采用全湍流模拟方式并不意味着流场驻点以后立刻产生湍流边界层,一般而言采用全湍流模拟方式得到的数值解本身是按照湍流模型自身定义的转捩位置而开始转捩的,只不过与试验的转捩位置相比较大大提前[5]。

图3 表面压力系数的比较(全湍流)Fig.3 Surface pressure coefficient(fully turbulent)

由图3中可以看出,采用两种湍流模型得到的缝翼、主翼和襟翼上的压力分布几乎相同,并均与试验结果吻合。两种湍流模型的数值模拟结果仅在襟翼的上表面存在细微的差别,SA模型的计算结果略低于SST模型的计算结果。采用两种湍流模型得到的总体气动特性存在比较明显的差别,两种湍流模型得到的升力系数相差0.08,阻力系数相差0.0016,相比较而言,SST模型得到的升力系数更接近试验结果。

图4给出了采用两种湍流模型得到的六个典型站位上的速度型及相应的试验结果(具体站位见图1)。由图中可见,采用全湍流方式得到的典型站位上的速度型与试验结果在定性上是接近的,定量上差别明显。在主翼的三个站位上数值模拟结果与试验结果的差别主要在于主翼的边界层偏厚和缝翼尾迹区速度偏低、宽度偏大三个方面,但两种湍流模型的结果彼此基本吻合。在襟翼的三个站位上,两种湍流模型的计算结果差别明显,在主翼尾迹区的模拟上,SST模型过低地预测了主翼尾迹区的速度,SA模型则与试验结果吻合较好；两种湍流模型均过低地预测了缝翼尾迹区的速度值、过高地预测了缝翼尾迹区的宽度,在最后一个站位上,SST模型的缝翼尾迹区的数值结果有所改善。总之,采用全湍流方式模拟该三段构型,主翼边界层厚度、缝翼的尾迹区和主翼的尾迹区的计算结果均与试验结果差别较大,SA模型在模拟主翼尾迹区的结果略优,SST模型则在模拟缝翼尾迹区上结果略优(襟翼站位上)。

3 模拟试验转捩位置的结果与分析

文献[6]中给出了相对于收缩构型弦长c的转捩区域(见表1)。其中试验测量值中“n/a”表示在缝翼下表面型面尖点以后、主翼下表面型面尖点以后和襟翼下表面均没有观察到确定的转捩位置。为了研究转捩位置对速度型模拟精度的影响,本文选用SST两方程数值模拟了试验的转捩位置,对应于试验值没有明确转捩位置的点,本文分别选择了缝翼下表面尖点前、主翼下表面尖点前一小段距离为转捩区域,而在襟翼下表面则为层流区域。

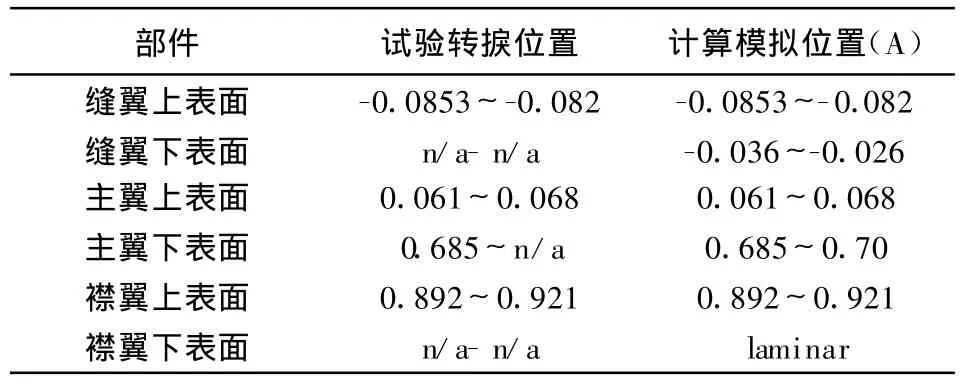
表1 计算与试验的转捩位置(α=19°)Table1 Transition location for calculation and test(α=19°)

表面压力分布的计算结果(本文没有给出)表明,模拟试验的转捩位置得到的压力分布与采用全湍流模拟方式得到的压力分布基本一致,且均与试验结果吻合良好,只是在襟翼的上表面模拟试验转捩位置后得到的压力系数略高于全湍流计算的结果和试验值,从本文以下的讨论中可以看出,这主要是由于襟翼上方边界层的掺混模拟的差别造成的。

图5给出了采用SST两方程模型是否模拟试验转捩位置的典型站位速度型的比较。模拟了试验的转捩位置后,典型站位的速度型得到了明显的改善。首先是主翼上边界层的厚度和与试验结果更加接近,其次是缝翼和主翼的尾迹区速度值和尾迹区的宽度均有明显改善,但与试验结果相比较还存在一定差距。

表2给出了采用两种湍流模型和是否模拟试验转捩位置得到的升力系数、阻力系数以及相应的试验值。可以看到,模拟了试验的转捩位置后,升力系数略有增加,阻力系数比全湍流方式降低了100个阻力单位(1阻力单位=0.0001)。

图5 典型站位速度型的比较(转捩位置A)Fig.5 Velocity profileon typical station(Transition location A)

表2 气动特性的比较(α=19°)Table2 Aerodynamic character(α=19°)

4 延迟转捩位置的计算结果与分析

从第3节的讨论中可以看到,模拟了试验的转捩位置后,虽然缝翼的尾迹区模拟精度有了比较明显的改善,但与试验结果之间依然存在较大的差距,本文作者认为缝翼上表面的边界层的产生和发展是决定其尾迹区模拟精度的主要原因之一。本节将讨论缝翼上表面转捩位置变化对其尾迹区发展的影响。

在数值模拟过程发现,将试验测定的缝翼上表面转捩位置进一步向下游方向移动而保持转捩区长度不变,缝翼上表面的逆力梯度会导致缝翼上表面头部出现较大范围的分离区。为了避免缝翼头部的分离,本文在数值模拟中采用了微吸气技术,微吸气的起始位置在缝翼头部顶点,终止位置在确定的转捩区之前。采用上述技术,本文将缝翼上表面的起始转捩位置向下游推迟到-0.073的位置(转捩位置B),而保持转捩区长度不变,其它的转捩参数与转捩位置A相同。

图6给出了采用SST两方程模型和转捩位置B的数值模拟结果,图中同时还给出了全湍流和转捩位置A的数值模拟结果。由图中可以看出,将转捩位置推迟到B点后,缝翼尾迹区的模拟精度有了进一步的提高,尤其是在图1中所示的前四个站位上(在x/c=0.1075站位上,试验结果可能存在误差[6])。本节和第三节的计算结果表明,SST模型具有较好的尾迹区模拟精度,导致计算与试验缝翼尾迹区速度型差异的主要原因不是湍流模型本身,而是缝翼上表面湍流边界层起始位置。

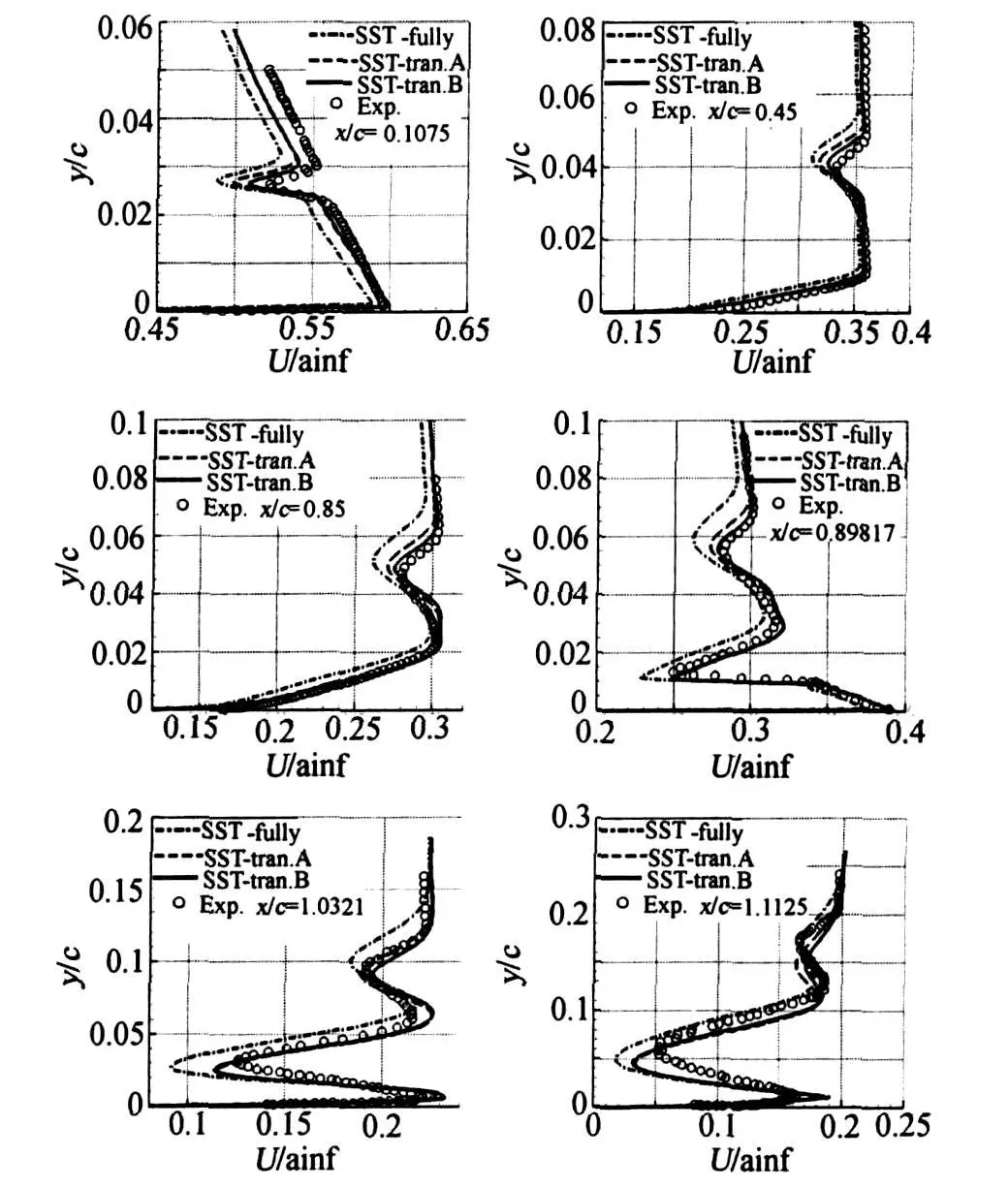
图6 典型站位速度型的比较(转捩位置B)Fig.6 Velocity profile on typical station(Transition location B)

5 结 论

本文采用TRIP2.0软件和结构对接网格技术,通过求解任意坐标系下的RANS方程,数值模拟了30P-30N三段翼型的复杂流场,主要研究了SA和SST两种湍流模型、转捩位置对数值模拟结果的影响。通过与相应的试验结果相比较,得到以下一些基本结论:

(1)采用全湍流模拟方式,两种湍流模型均可以较好地模拟该多段翼型的压力分布,但速度型的计算结果与试验结果差别明显；

(2)模拟试验的转捩位置,对压力分布的计算结果影响较小,对气动力系数,尤其是阻力系数影响显著；可以明显提高速度型的数值模拟精度,但缝翼尾迹区的计算精度仍然与试验结果存在明显差距；

(3)采用微吸气技术推迟缝翼的转捩位置,可以进一步提高缝翼尾迹区的数值模拟精度；

(4)本文采用的湍流模型本身具有较强的尾迹模拟能力,转捩位置是导致计算与试验在速度型上差异的主要因素之一。

[1]TINOCO E N,BOGUE D R.Progress toward CFD for full flight envelope[J].Aeronautical Journal,2005,109:451-460.

[2]PAUL L JOHNSON,KENNETH M JONES,MICHAEL DMADSON.Experimental investigation of a simplified 3D high lift configuration in support of CFD validation[R].AIAA 2000-4217.

[3]STUART E ROGERS,KARLIN ROTH,STEVEN M NASH.CFD validation of high-lift flows with significant wind-tunnel effects[R].AIAA 2000-4218.

[4]朱自强,陈迎春,吴宗成等.高升力系统外形的数值模拟计算[J].航空学报,2005,26(3):257-262.

[5]CHRISTOPHER L RUMSEY,SUSAN X YING.Prediction of high lift:Review of present CFD capability[J].Progressin Aerospace Sciences,2002,38:145-180.

[6]CHRISTOPHER L RUMSEY,THOMAS BGATSKI,SUSAN X YING,et al.Prediction of high-lift f lows using turbulent closure models[R].AIAA-97-2260.