基于层次分析法的和谐校园评价指标权重确定

王鹏 彭元伟 全美杰 刘文洁 张莎娜 何享

衡阳师范学院资源环境与旅游管理系 421008

基于层次分析法的和谐校园评价指标权重确定

王鹏 彭元伟 全美杰 刘文洁 张莎娜 何享

衡阳师范学院资源环境与旅游管理系 421008

1.层次分析法及其基本流程

层次分析法[1-3]（Analytic Hierarchy Process，简称 AHP）是美国运筹学家T. L. Saaty 教授于上世纪 70 年代初期提出的一种简便、灵活而又实用的多准则决策方法。这是一种定性和定量相结合的、系统化的、层次化的分析方法。它是将复杂问题分解为多个组成因素，并将这些因素按支配关系进一步分解，按目标层、准则层、指标层排列起来，形成一个多目标、多层次的模型，形成有序的递阶层次结构。通过两两比较的方式确定层次中诸因素的相对重要性，然后综合评估主体的判断确定诸因素相对重要性的总顺序。层次分析法的基本思想就是将组成复杂问题的多个元素权重的整体判断转变为对这些元素进行“两两比较”，然后再转为对这些元素的整体权重进行排序判断，最后确立各元素的权重。具体流程如图1。

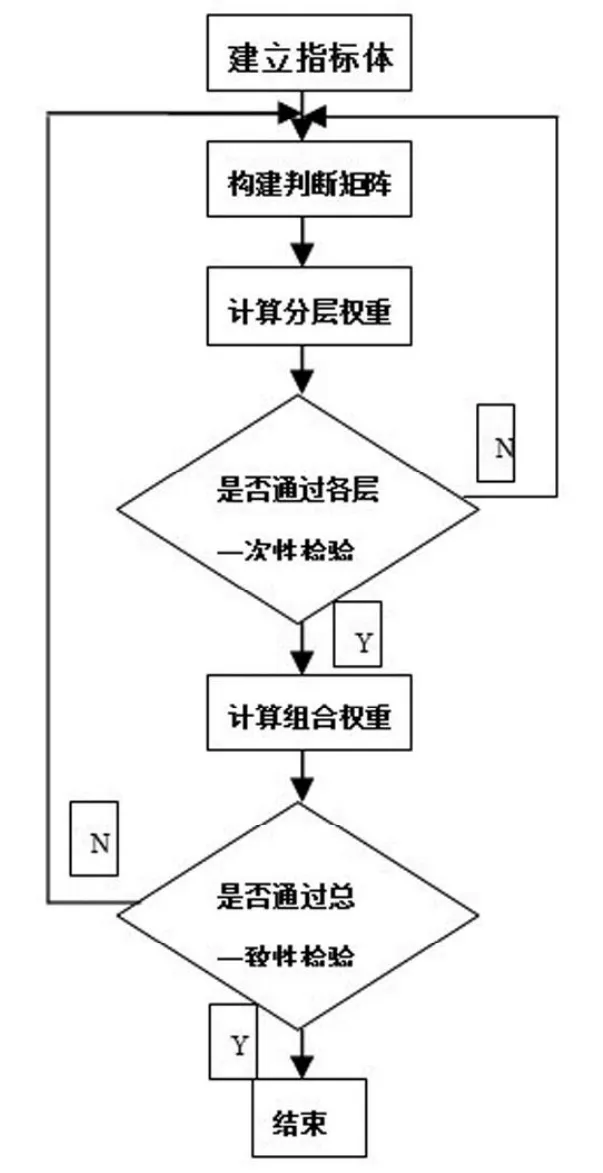
图1 层次分析法流程图Fig. 1 Flow chart of analytic hierarchy process

2.和谐校园评价指标权重的确定

2.1 造建层次分析模型

对问题所涉及的因素进行分类，构造一个各因素之间相互联结的递阶层次结构。处于最上面的层次一般是问题的预定目标，通常只有一个元素，中间层的元素一般是准则层和子准则层，最低层一般是方案层[1]。和谐校园评价指标体系分三层，第一层为和谐校园这一总目标A，第二层包括发展战略的和谐B1、规章制度的和谐B2、人际关系的和谐B3、育人环境的和谐B4及日常管理的和谐共五项指标，每项指标下面又包含的若干个子指标项作为第三层。整个和谐评价指标体系如表1所示。

2.2 构造判断矩阵

(1)本研究采取专家调查问卷的形式 ,请多位专家在构造判断矩阵前对层次结构中各生态指标进行重要性单排序 ,以便减小误差 ,一次性通过一致性检验。

(2)在每一层次上,对该层指标进行逐对比较,写出数值判断矩阵为:

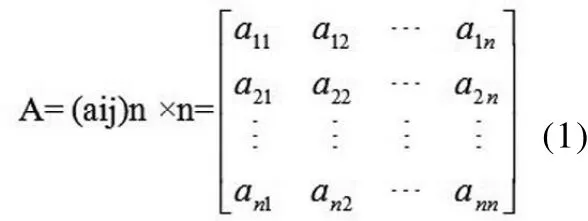
表1 和谐校园评价指标体系Table1 Harmonious campus evaluation index system

表 2 标度及其描述[3]Table.2 Number scale and its description

设有因素 x1 , x2 , …, xn ,每次取两个因素 xi, xj,用正数 aij表示 xi 与 xj 的重要性之比,由 Saaty的1-9法确定,见表2。其中aij必须满足aij=1/aij(i≠j) (I，j=1，2......n).aij=1 (i=j)，A矩阵具有互反性和基本一致性，根据各指标的重要性构造判断矩阵进行计算，所得结果如下表所示，见表3～8。

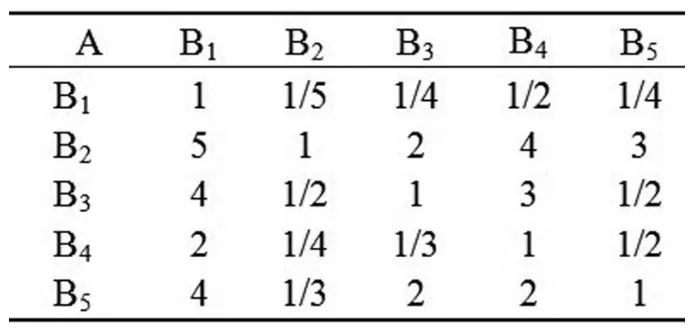
表3 判断矩阵A-BTable 3 Judgment Matrix A-B

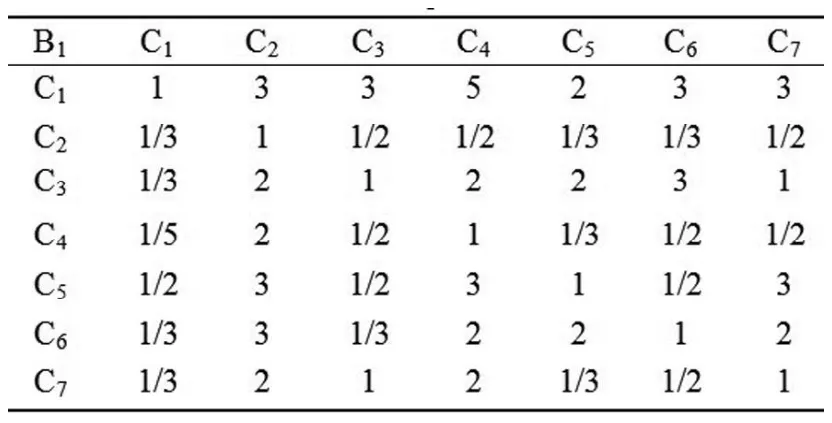
表4 判断矩阵B1-CTable 4 Judgment Matrix B1-C

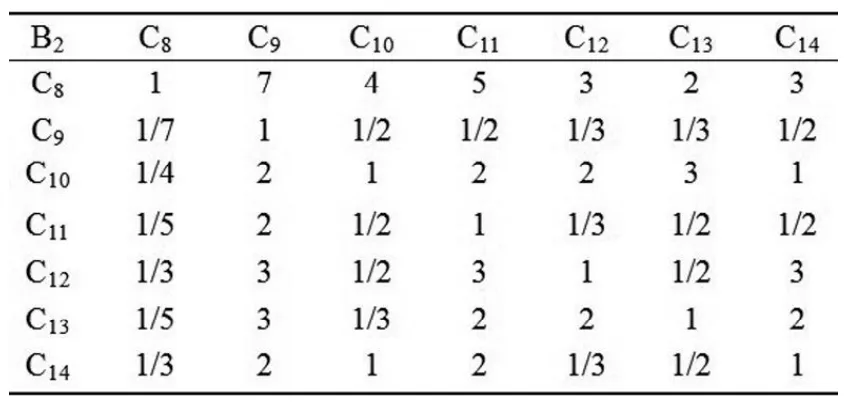
表5 判断矩阵B2-CTable 5 Judgment Matrix B2-C

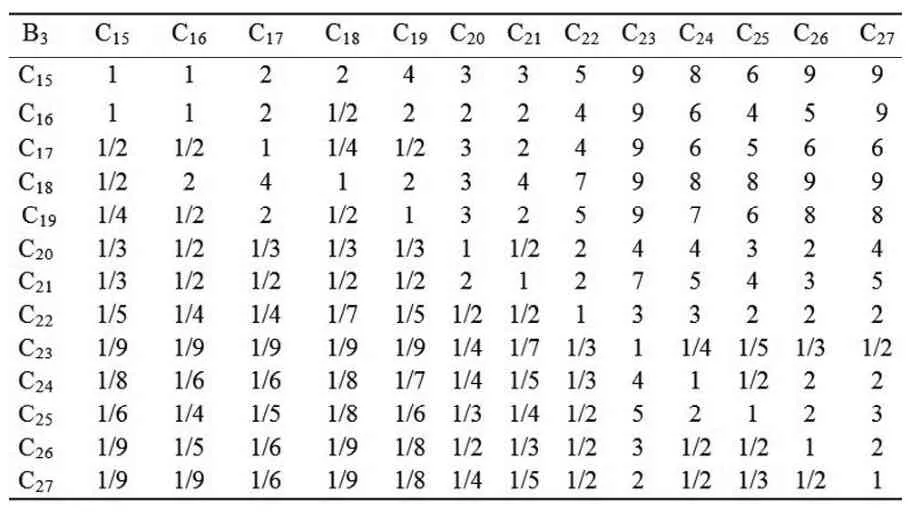
表6 判断矩阵B3-CTable 6 Judgment Matrix B3-C

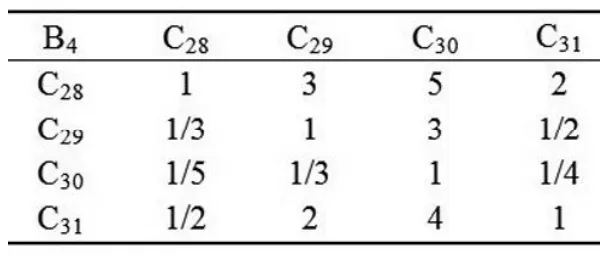
表7 判断矩阵B4-CTable 7 Judgment Matrix B4-C

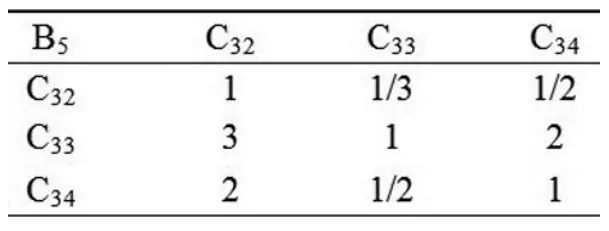
表8 判断矩阵B5-CTable8 Judgment Matrix B5-C

（3）计算权向量并做一致性检验

对于每一个成对比较阵计算最大特征根及对应特征向量，利用一致性指标、随机一致性指标和一致性比率做一致性检验。若检验通过，特征向量(归一化后)即为权向量：若不通过，需重新构追成对比较阵。

①计算权重

第一步：将表1中A的元素各行相加（如表9）

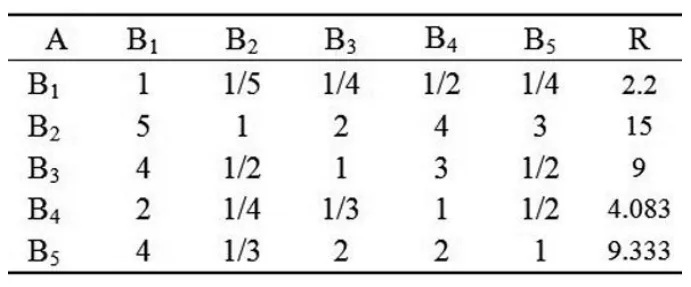
表9 判断矩阵A-BTable 9 Judgment Matrix A-B

第二步：将相加后的向量归一化即得权重向量。WB(055533，0.378635，0.227181，0.103064，0.235587)T，，

②一致性检验:

第一步：计算判断矩阵的最大值λA

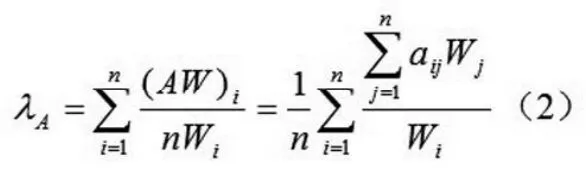
将矩阵A-B的Wi和AWi代入（2）得：5.22179

第二步：计算衡量一个成对比矩阵A不一致程度的指标CI：

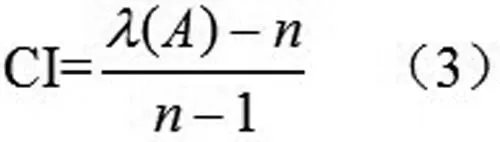
将矩阵A-B的λA代入（3）得：0.055447

从表10中可查出检验成对比较矩阵A 一致性的标准RI：RI=1.12

第三步：按下面公式计算成对比较阵 A 的随机一致性比率 CR：当CR<0. 1时，判定矩阵 A 具有满意的一致性，或其不一致程度是可以接受的；否则就调整成对比较矩阵 A，直到达到满意的一致性为止，

表10 平均随机一致性指标R.I.Table 10 R.I. Mean Random Consistency Index

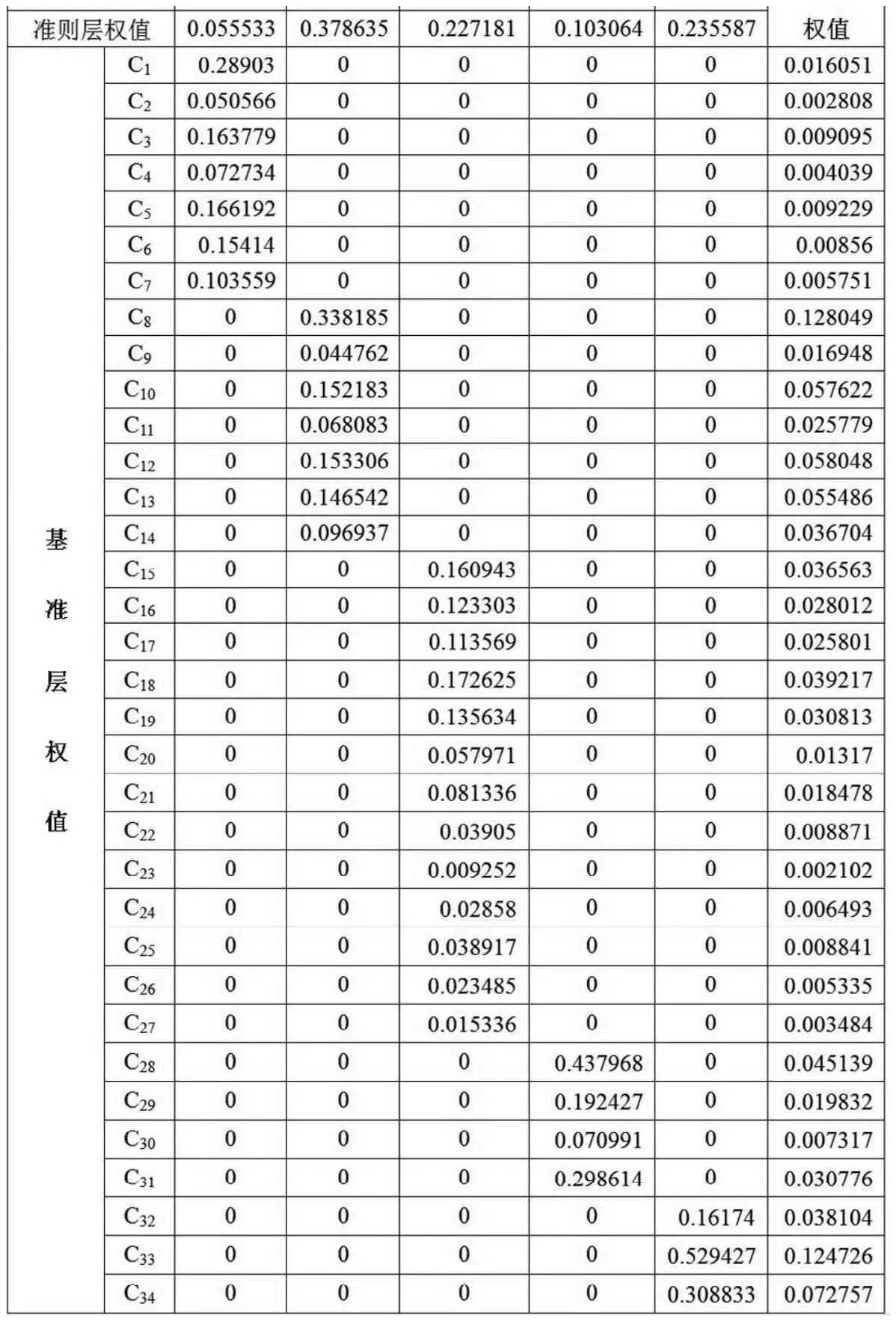
表11 层次总排序Table 11 Levels of total sort

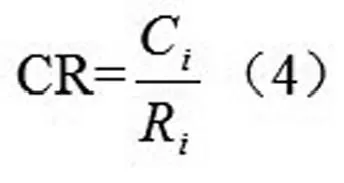
把Ri和Ci代入（4）得：0.049507

因为CR＜0.1，所以矩阵A具有满意的一致性。

同理可得，矩阵B1，B2，B3，B4,B5的CR分别为（0.080596，0.072375，0. 063063，0.027522，0.010408）均小于0.1，所以矩阵B1，B2，B3，B4都具有满意的一致性。

（4）计算组合权向量

上面得到的是一组元素对其上一层中某元素的权重向量。最终要得到各元素，特别是最低层中各元素对于目标的排序权重，即所谓总排序权重。总排序权重要自上而下地将单准则下的权重进行合成，并逐层进行总的判断一致性检验。

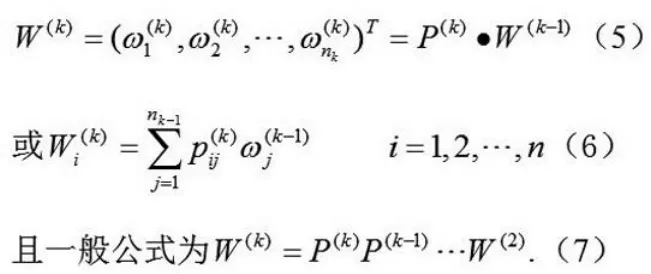
由（5），（6）或（7）式可得表11。

3.结论

和谐校园评价指标体系是一个多层次、多指标的复合体系，在这个复合体系中，各层次、各指标层的相对重要性各不相同，难以科学确定，常用的专家确定法经验、估值法等方法难以奏效。层次分析法通过构造判断矩阵，先对单层指标进行权重计算，然后再对层次间的指标进行总排序，来确定所有指标因素对于总指标的相对权重，为确定类似评价指标体系权重提供了一种较好的解决途径。层次分析法的利用，不仅可以降低评估难度，提高指标权重的精确度和科学性，而且通过采取对判断矩阵进行一致性检验等措施，有利于提高权重确定的信度和效度。

[1]彭国甫，李树丞，盛明科.应用层次分析法确定政府绩效评估指标权重研究[J].中国软科学,2004,(6)：136-139

[2]蔡海鹏,杨坤玉. 基于层次分析法的数字化校园评价指标权重确定[J].长沙航空职业技术学院学报,2005,5(2)：58-63 [3]崔萌,张宏伟,王媛,雷鸣,钟定胜.基于层次分析法的生态校园评价体系[J].天津工业大学学报,2007,26(4)：81-85

Determining the Evaluation Criterion Weight of Harmonious Campus Based on AHP

WANG Peng ,Peng Yuanwei ,QUAN Meijie ,LIU Wenjie,ZHANG Shana ,HE Xiang
(The Department of Resource Environment and Tourism Management ,Hengyang Normal University,Hengyang 421008 ,Hunan,China)

确立包括科学的指标权重在内的评价指标体系，是和谐校园评价顺利完成和提高评价结果信度和效度的关键。层次分析法（AHP）为准确确定和谐校园评价指标间权重提供了可行的途径。要准确评价校园的和谐度，指标权重是关键因素，确定评估指标权重时，应重点考虑指标彼此间重要性的量化。

和谐校园；指标体系；层次分析法；权重

The establishment of evaluation indexes system, including scientific weights of index, is the key to successful completion of the assessment of a harmonious campus and improve the reliability and validity of the assessment results. The AHP method provides a practical way to determine the weight of the precise evaluation indexes of harmonious campus. To take An accurate assessment of level harmony on campus, the weight of indexes is the critical factor. When determining the weight of the assessment indexes, quantify the importance between the various indicators should be key consideration.

harmonious campus;index system; analytic hierarchy process；weight

10.3969/j.issn.1001-8972.2010.14.126

湖南省大学生研究性学习与创新性实验计划项目。

王鹏（1965-），男，湖南祁东人，教授，博士，主要研究方向：土地利用，旅游地理学；

彭元伟（1987-），男，湖南保靖人，衡阳师范学院地理科学专业本科生。