辅助墩对预应力混凝土斜拉桥动力特性的影响

费 梁 谢敏杰 姜长宇

随着现代工程技术和物理学的发展,斜拉桥跨径不断增大,结构刚度越来越柔,桥梁结构动力分析已经具有非常重要的工程应用价值。桥梁结构振动,是伴随着外作用输入(车辆动荷载、风力、地震波)和摩擦损耗(材料内摩擦和连接及支承的摩擦),结构体系的变形能量和运动能量相互转换的周期性过程。桥梁结构的动力特性包括自振频率、主振型及阻尼等,是结构本身固有的,反映桥梁的刚度指标,取决于结构的组成体系、刚度、质量分布及支承边界条件等,它对于正确地进行桥梁的抗震设计、抗风稳定性分析及维护有着重要的意义。本文以开口截面的约束扭转理论为基础,建立π形截面混凝土斜拉桥的动力模型,考虑边跨有辅助墩和无辅助墩两种结构形式,分析南太湖大桥的动力特性。

1 工程概况

湖州南太湖大桥是湖州三环北路东延工程中的一座大型桥梁,主桥为(160+190+38)m独塔双索面混凝土斜拉桥,引桥为多跨等截面预应力混凝土连续箱梁。

湖州三环北路东延工程是湖州市城市路网规划中的重要组成部分,位于湖州市市区北部,是行政中心连接申苏浙皖高速公路、湖州织里镇的重要城市快速干道。

南太湖大桥西接湖梅立交,向东跨过小梅港和长兜港。桥位处两条河流并行,中间为狭长陆地。

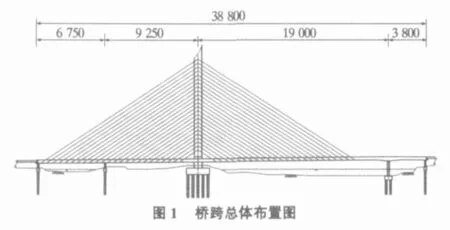
南太湖大桥主桥为双索面、H形独塔、混凝土斜拉桥,跨径布置为160 m边跨+190 m主跨+38 m外伸孔(即协作体系),主桥总长388 m。其中边跨160 m被辅助墩分为67.5 m+92.5 m。拉索布置形式为竖琴式。190 m主跨跨过长兜港主航道,160 m边跨跨过中间狭长陆地及小梅港,主墩落在狭长陆地上且靠近主河道(见图1)。

2 斜拉桥空间有限元模型

斜拉桥动力特性分析中常用的模型如下:1)单主梁模型,即主梁带刚臂的鱼骨梁模型。这种模型的精度主要取决于纵、横梁的刚度,一般用于扭转刚度较大的全封闭箱梁结构。2)双主梁模型。它是将主梁截面的质量和刚度平均分配在两个纵梁上,更接近于实际,但是这种模型在实际应用中由于对扭转刚度不能很好地模拟,因此分析的斜拉桥动力特性精度不高。3)三梁式模型。该模型能够有效地考虑约束扭转刚度,与实际吻合较好,不过对结构刚度和质量的分布不是很准确。4)空间板壳模型。这个模型模拟主梁使箱形结构的斜拉桥可以达到很好的效果,但所需机时较多,随着现代计算机技术的发展,用空间板壳模型进行分析逐渐成为可能。

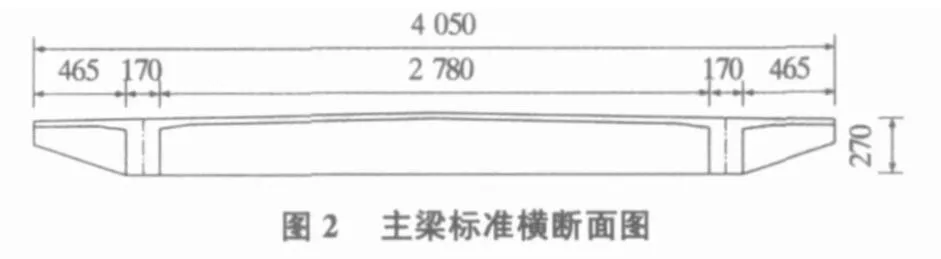
对该斜拉桥来说,其主桥横截面为π形的双边主梁形式,如图2所示,这里将采用空间梁—壳单元组合的方式来建立该斜拉桥的空间有限元模型。用壳单元模拟主肋、桥面板以及横隔板,桥塔采用空间梁单元建立,拉索锚固点为梁单元和壳单元的节点,斜拉索用杆单元来模拟,按修正弹性模量Ernst公式来考虑几何非线性的影响。这样的梁—壳单元模型完全按照真实桥梁的组成来模拟,并且不考虑桥面铺装、防撞护栏、人行道栏杆等二期恒载对桥梁结构刚度的作用,通过修改桥面板的材料密度来考虑二期恒载的附加质量,因而可以较为真实地反映桥梁结构的实际几何关系及质量分布。最终建立的斜拉桥空间有限元模型如图3所示。

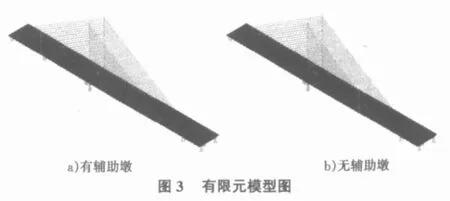
典型的无阻尼模态分析求解的基本方程是经典的特征值问题:

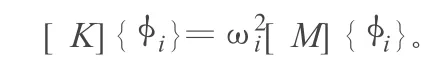
其中,[K],[M]分别为刚度、质量矩阵;{φi}为第i阶模态的振型向量(特征向量);ωi为第i阶模态的固有频率。

利用ANSYS提供的Block Lanczos(分块兰索斯)法特征值求解器计算,Lanczos算法是用一组向量来实现 Lanczos递归计算。当计算某系统特征值谱所包含一定范围的固有频率时,采用分块兰索斯(Block Lanczos)法提取模态特别有效。计算时,求解从频率谱中间位置到高频端范围内的固有频率时的求解收敛速度和求解低阶频率时基本上一样快,特别适用于大型对称特征值求解问题。

3 动力特性分析

由于空间斜拉索的存在,斜拉桥的弯曲和扭转强烈耦合在一起,几乎不存在单纯的扭转振型,而只有弯曲为主兼有扭转的振型,或者以扭转为主兼有弯曲的振型,因此,对斜拉桥的动力分析,必须采用三维空间模型。采用成桥状态进行该桥的动力特性分析,斜拉索内力和结构质量均采用成桥状态时的数值,采用的边界约束条件为:

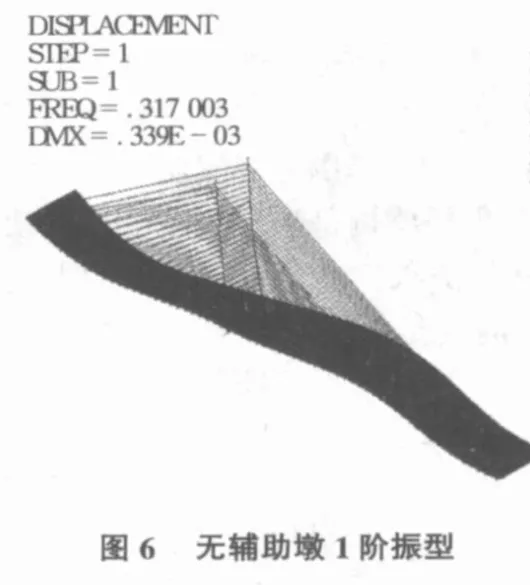
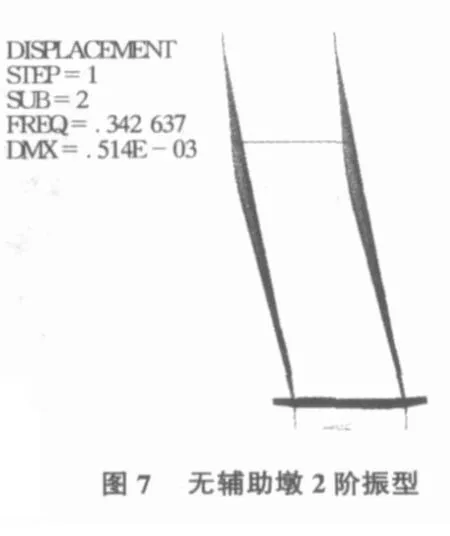
1)桥塔、辅助墩及边墩均与基础固结;2)主梁与边墩、辅助墩交接处,主梁的横向线位移、竖向线位移及绕纵轴的扭转自由度由边墩约束,其余自由度均释放;3)塔梁墩结合处,主梁与主塔及主墩固结。考虑边跨有辅助墩和无辅助墩两种方式,主桥的前6阶无阻尼自振频率以及相应振型的主要特点见表1,前2阶振型图如图4～图 7所示。

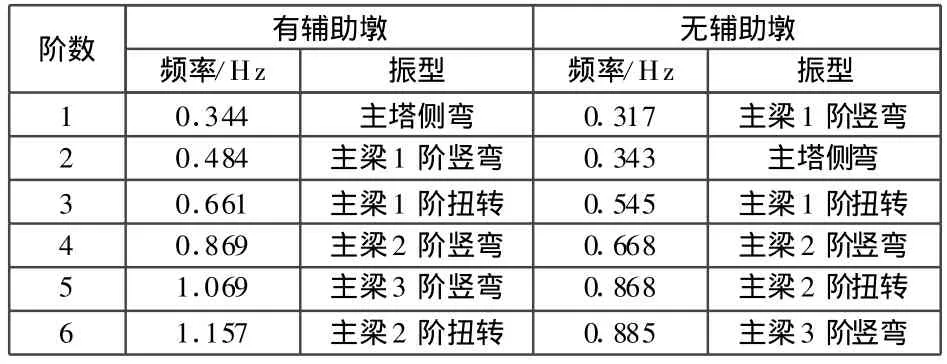
表1 前6阶自振频率及振型比较表

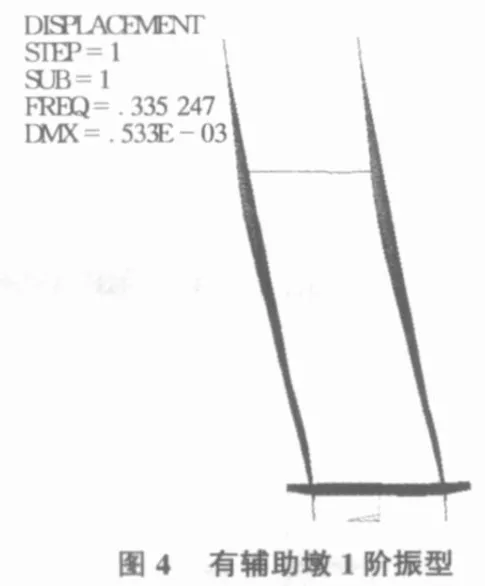
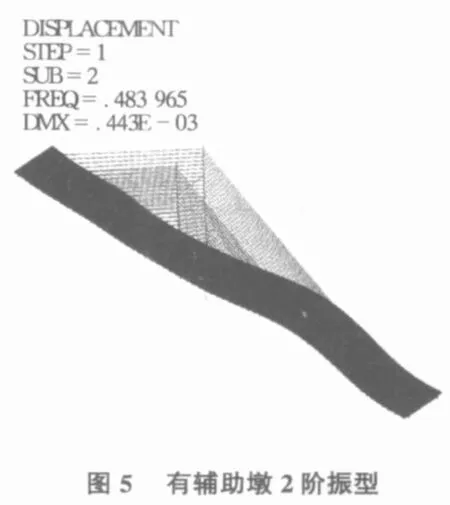
斜拉桥的动力特性分析是研究斜拉桥动力行为的基础,其自振特性决定其动力反应的特性。1阶竖弯振型对桥梁的地震响应和抗风稳定性有较大的影响;1阶横弯振型对桥梁在风荷载作用下的侧向位移等影响很大;1阶扭转振型在桥梁的颤振中占主要成分,是影响桥梁空气稳定性的主要因素。因此1阶竖弯频率、1阶侧弯频率和1阶扭转频率对桥梁结构的抗震性能和抗风性能具有重要的意义。通过对南太湖大桥有无辅助墩两种不同的结构形式的动力特性分析可得:

1)从静力角度来看,边跨设置辅助墩可以提高结构的整体刚度,减小活载作用下塔底的内力、塔顶顺桥向位移和主梁的竖向位移;从动力角度来看,边跨设置辅助墩对主梁的振动起了强大的约束作用,1阶竖弯有辅助墩频率高于无辅助墩频率。2)南太湖大桥的主塔侧弯振型出现较早,说明主塔的结构比较纤细。3)大桥的主梁竖弯振动基频为0.484 Hz,远低于载重汽车2 Hz～5 Hz的激振频率,表明全桥的结构参数设计是合理的,动力特性良好,具有较好的抗震、抗风性能。4)虽然本桥采用了抗扭刚度较低的π形双边主梁断面,但是由于桥面较宽,斜拉索采用空间密索体系,墩塔梁固结,使该桥的整体刚度较高。

4 结语

1)由以上分析可知:有无辅助墩对整体振型的出现次序及对应频率影响较大,辅助墩的设置使得南太湖大桥的整体刚度有较大的提高,改善了结构的动力性能。2)该桥主梁竖弯和扭转振动出现较早。在斜拉桥的前6阶振型中,以主梁的竖向弯曲和扭转振动为主,这也是符合该桥的实际情况的。该斜拉桥结构纵向轻柔,从而使得桥面竖向弯曲振动出现较早,同时桥梁主梁的横截面为π形的开口式双边主梁,抗扭性能要比全封闭式的箱形截面弱,这使得桥面的扭转振动也会出现得比较早。3)建模是结构分析的关键,模型对结构刚度和质量分布模拟准确与否,严重影响计算的精度。在建立有限元模型时应尽可能的反映结构的空间位置、尺寸、质量、材料特性、连接形式、初始内力和初始变形等,在此基础上建立空间三维有限元模型。

[1]范立础.桥梁抗震[M].上海:同济大学出版社,1997:117-154.

[2]刘士林,梁智涛.斜拉桥[M].北京:人民交通出版社,2002:36-94.

[3]李国豪.桥梁结构稳定与振动(修订版)[M].北京:中国铁道出版社,1996:388-396.