亚波长闪耀光栅矢量衍射效率计算

曹艳波,艾 华

(中国科学院长春光学精密机械与物理研究所,吉林长春 130033)

1 引 言

闪耀光栅是一种能将单个刻槽面衍射的中央极大和诸槽面间干涉零级主极大分开的相位型光栅。闪耀光栅的刻槽面与光栅面不平行,两者之间有一夹角 (称为闪耀角),从而使单个刻槽面(相当于单缝)衍射的中央极大和诸槽面间 (缝间)干涉零级主极大分开,将光能量从干涉零级主极大,即零级光谱,转移并集中到某一级光谱上去,实现该级光谱的闪耀[1]。而闪耀光栅的衍射效率理论上可以利用基于惠更斯-菲涅耳原理和基尔霍夫积分的标量衍射理论进行计算,但结果只是近似,特别是对于微小尺寸光栅,无法避免由于入射光的偏振态而造成的偏差。矢量衍射理论主要针对处于共振区域或亚波长区域的光栅,耦合波方法是目前广泛使用的一种矢量衍射理论,由M.Moharma率先提出,20世纪 90年代在稳定性、收敛性和计算效率方面得到不断完善[2,3]。矢量衍射理论的基础是严格电磁波理论,即通过在适当的边界条件上严格地求解 Maxwell方程组,严格耦合波分析算法 (Rigorous Coupled Wave Analysis,RCWA)是通过在适当的边界条件上严格地求解Maxwell方程组来数值分析光栅的衍射问题。

本文提出将矢量衍射数值算法—严格耦合波分析应用于亚波长闪耀光栅衍射效率的计算,介绍了如何利用严格耦合波算法来分析光栅的衍射问题。以金属铝闪耀光栅为例进行了衍射效率的分析计算,得到其衍射效率在 TE偏振态下可达到 90%以上,并在 -5衍射级次上产生闪耀。

2 矢量衍射算法—严格耦合波分析

耦合波理论主要包括 3个步骤:(1)由Maxwell基本方程组求得入射区域及透射区域电磁场的表达式,但这往往可以由 Rayleigh展开式直接给出;(2)将光栅区域内的介电常数及电磁场用傅里叶级数展开,并由 Maxwell基本方程组推导出耦合波方程组;(3)在不同区域边界面上运用电磁场边界条件,通过一定的数学方法求得各级衍射波的振幅及衍射效率。耦合波将电磁场按衍射级次展开,因而耦合波方法涉及到的数学理论更为简单。

由于 TE和 T M两种偏振的分析计算方法相同,本文只分析 TE偏振态波入射的情况。电场矢量平行于刻槽方向,设入射平面波的波长为λ0,由于在入射区 1和透射区 2(如图1所示)介电常数为常数,根据 Rayleigh展开式[2],两个区的电场分布为:

图1 一维矩形衍射光栅示意图Fig.1 Schematic diagram of one d imension rectangle diffraction grating

式中Rm和Tm分别为第m级后向衍射和前向衍射的归一化电场振幅,d为光栅刻槽深度,k0为入射光在真空中的波矢。kxm=k0[n1sinθ+m(λ0/T)];kl,zm=;l=1,2;kxm,kl,zm只能为正实数或负虚数。

通过计算矩阵的特征值和特征向量来求解严格耦合波方程[3]:

式中qi和wm,i分别为矩阵 A的特征值的正平方根和特征向量;gm,i为矩阵 G的元素,G=WQ,Q为对角矩阵,元素qi,系数由边界条件确定。代入边界条件方程,并根据定义,可以得出光栅的衍射效率为:

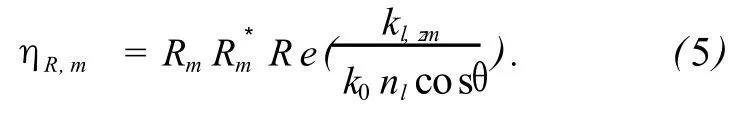
对于不规则结构的闪耀光栅,可以将其分为若干层,每一层当作是一个矩形光栅,从而任意面形光栅可由若干占空比不同、周期相同的矩形光栅进行依次叠加来近似,矩形越小,层数越多,简化结构越接近实际结构,计算结果更精确,但是也会影响到计算结果的收敛性,如图2所示。

图2 闪耀光栅的二维简化计算模型Fig.2 Two d imension simplyfied model of blazed grating

对于任意的第l层,考虑到算法的继承性,直接从第l层的 TE偏振电场和磁场空间谐波振幅开始算起:

式中di为第i层的厚度,Dl=dk,其他参数如前所述。迭代计算即可求出复杂多层结构的衍射效率,对于计算过程中出现的数值不稳定性问题,可以采用增强透射矩阵算法得到较好的解决[4],通过带入边界条件,可以得到多层结构的综合算式:

式中 X,Y1和 Y2都为对角矩阵,其对角元素分别为 exp(-k0qid),k1,zi/k0和k2,zi/k0,由此式也可以得出透射效率的计算结果。

3 闪耀光栅衍射效率的计算分析结果

利用上述严格耦合波分析算法,对亚波长闪耀光栅进行分析计算。分析对象为将二氧化硅表面镀的纯金属铝膜刻蚀而成的楔形闪耀光栅,光栅的截面几何结构如图3所示。光栅参数为:闪耀角β=11.3°,光栅常数d=500 nm。

图3 闪耀光栅截面尺寸折射率云图Fig.3 Contour map of cross-section profile of blazed grating

由于计算分析的谱段为可见光范围,金属材料对可见光的吸收率大,而且折射率随波长变化比较大,金属铝在可见光波段内的折射率如表1所示[5],而底层材料二氧化硅对可见光的折射率可以近似为常数,约为 1.45。

表1 可见光范围内金属铝不同波长的折射率[5]Tab.1 Refractive indice of alum in ium in VIS spectral coverage[5]

通过简化结构后对该光栅进行计算,可以得到光栅各级衍射效率 (包括反射、透射和吸收,由于金属介质对可见光波段的消光系数大,透射为零),多层光栅结构周期相同,占空比不同,在入射角为闪耀角 (即θ=11.3°)时,分别计算 TE和T M两种偏振态下的衍射效率。各级衍射效率之和 (±6级)如图4所示,对应级次为 -5的衍射效率的闪耀方向如图5所示。

图4 入射角为闪耀角时计算的各级衍射效率之和Fig.4 Total diffraction efficiency when launch angle is a blazed angle

图5 入射角为闪耀角时 -5级次的衍射效率Fig.5 Diffraction efficiency of-5 order when launch angle is a blazed angle

从结果可以看出,在可见光谱段内,TE偏振态的衍射效率要高于 T M偏振态,衍射效率主要集中在 0级,但是在 -5级出现闪耀,同样级次在短波段范围内,T M偏振态的衍射效率略高于 TE偏振态 (除了个别奇异点外,二者趋于一致)。

利用标量衍射的算法对该结构进行计算[1],结果如图6和图7所示,在入射条件和计算的衍射级次不变的前提下,不考虑入射光的偏振态,得出闪耀的衍射级次和总的衍射效率,可以得到相同的衍射效率结果 (由于波长/光栅常数比不在标量衍射计算范围),计算结果必然存在很大偏差[6,7]。

图6 标量衍射计算的各级衍射效率之和Fig.6 Total diffraction efficiency using scalar diffraction computingmethod

图7 标量衍射计算的 -1级次的衍射效率Fig.7 Diffraction efficiency of-1 order using scalar diffraction computingmethod

4 结 论

本文将矢量衍射数值算法—严格耦合波分析应用于亚波长闪耀光栅衍射效率的计算,该方法能够计算任意复杂轮廓光栅,通过细分分层,可以得到光栅基本单元,各层之间通过增透矩阵算法来实现多层的传递计算,结果相对于标量衍射计算方法能得到更加精确的结果。对于亚波长闪耀光栅在可见光范围内以闪耀角入射时的各级衍射效率进行计算,得到其衍射效率在 TE偏振态下可以达到 90%以上,并在 -5衍射级次上产生闪耀。矢量衍射数值算法可以适用于刻线更加致密的闪耀光栅,可以得到精确的衍射效率分析计算结果。

[1] 赵博,宴磊,李颜青,等.闪耀光栅的傅里叶分析 [J].光学技术,2001,27(2):103-108.ZHAO B,YAN L,L I YQ,et al..Analysis of blazed gratings with Fourier optics[J].Opt.Technique,2001,27(2):103-108.(in Chinese)

[2] MOHARAM M G,GRANN E B,POMMETD A,et al..Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings[J].J.Opt.Soc.Am.A,1995,12(5):1068-1076.

[3] LALANNE P. Improved formulation of the coupled-wave method for two-dimensional gratings[J].J.Opt.Soc.Am.A,1997,14(7):1592-1598.

[4] MOHARAM M G,POMMET D A,GRANN E B,et al..Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings:enhanced trans mittance matrix approach[J].J.Opt.Soc.Am.A,1995,12(5):1077-1086.

[5] EDWARD D P.Handbook of Optical Constants in Solids[M].New York:Academic Press,1985.

[6] 李娜娜,安志勇,崔继承.中阶梯光栅光谱仪光学系统的安装及检测[J].光学精密工程,2009,17(3):531-536.L IN N,AN ZH Y,CU IJ CH.Aligning and testing of optical system of echelle spectrography[J].Opt.Precision Eng.,2009,17(3):531-536.(in Chinese)

[7] 张善文,巴音贺希格.宽波段金属光栅设计中闪耀波长对光栅异常的补偿效应[J].光学精密工程,2009,17(5):990-1000.ZHANG SHW,Bayanheshig.Compensating effectof blazedwavelength to grating anomalies in design of broad bandmetallie diffraction gratings[J].Opt.Precision Eng.,2009,17(5):990-1000.(in Chinese)