用于相移点衍射干涉仪的加权最小二乘相位提取算法
2010-11-06于杰
于 杰
(中国科学院长春光学精密机械与物理研究所,吉林长春 130032)
1 引 言
传统的干涉条纹测量方法都是通过直接判断干涉条纹或者确定其序号来计算被测量。由于受到条纹判断准确性以及其他一些因素的影响,这种方法精度有限,不能满足高精度光学检测的要求。自从 1974年 Bruning提出移相干涉技术以来[1,2],移相干涉技术有了广泛的应用。这种技术能够减小噪声的影响,在干涉条纹对比度不好的情况下也能获得较好的结果,降低了光强分布不均匀对测量精度的影响,避免了激光高斯分布带来的影响。实现这种技术的关键之一是利用相位提取算法计算待测的相位分布[3]。
移相相位提取算法发展至今已有多种模式,标准移相算法要求移相量是一个已知量并且要求等间隔移相,这个要求一般很难满足。为降低算法对移相方式的严格要求,Novak提出了几种移相量为任意值的等间隔多步移相算法,并且通过理论分析和仿真实验找到每一种算法的最佳移相量,当移相量为最佳移相量时相位误差最小[4,5];Shouhong Tang提出了一种相移量为已知量的非等间隔五步移相算法[6];L.Z.Cai,Q.Liu和 X.L.Yang提出两种任意随机移相相位提取算法[7,8]。这些算法虽然对某种特定误差有较强的抑制能力,但是对于其他的误差抑制能力较弱,不能满足超高精度面形检测的要求。针对这一问题,本文引入一种权重待定的加权最小二乘算法。通过在最小二乘算法中添加待定的权重,分析移相干涉技术中多种误差源对算法的影响,得到多组约束方程,通过求解约束方程确定权重从而确定算法。
2 权重待定最小二乘法算法设计
移相干涉测量时,测量光和参考光相干形成干涉场的光强分布可表示为[9]:

式中A(x,y)为背景光强,B(x,y)为调制光强,φ(x,y)为待求解的相位分布,它由待测光学波面面形决定,δn(x,y)为引入的相位差。通过微位移PZT控制系统移动待测镜,在参考光和测试光之间引入相位差改变δn(x,y),获得多组干涉图以求解出 φ(x,y)。令:

式 (1)可化简为:

求解得到系数Bsin(x,y)和Bcos(x,y),待求的相位分布可表示为:
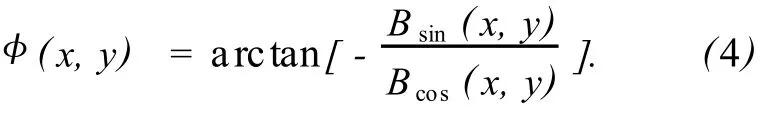
设定In(x,y)代表实际采集的移相干涉图,并假设每一幅干涉图对应的权重为wn,误差函数ε可表示为:

对等式 (5)分别求A,Bcos,Bsin这 3个参量的偏导数,当 3个偏导数为零时误差函数受这 3个
参量变化的影响最小[6],由此得到:

如果权重能满足:

由式 (6)得到待测相位为:
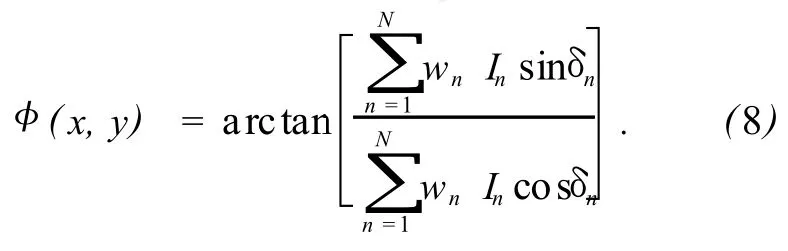
当式 (8)中的权重取不同的值时,算法对于各项误差的敏感程度不同,通过分析各种误差的影响得到约束条件,可最终确定待定系数。影响相位提取算法的误差主要包括 PZT移相不准,CCD的响应非线性和量化误差,光源的不稳定性和振动等等。
目前常用的相位提取算法是标准四步算法和Hariharan五步算法[10],其优点是对一些系统误差敏感度小,并且由于采集的干涉图比较少,数据采集时间短,后期的数据处理也相对简单。
标准四步算法和 Hariharan五步算法的表达式分别为:

2.1 PZT移相不准
在移相干涉技术中,移相不准是主要的误差源之一[11],它是由移相器本身的缺陷造成的。移相不准分为线性移相不准和非线性移相不准,前者是移相器标定后的残余线性误差,后者是由于PZT本身的非线性造成的。当存在线性和二阶非线性移相不准时,实际移相量可用理想移相量的多项式表示。实际移相量与移相不准Δ δn可表示为:

仅仅存在移相不准时,可得到相位误差Δφ:
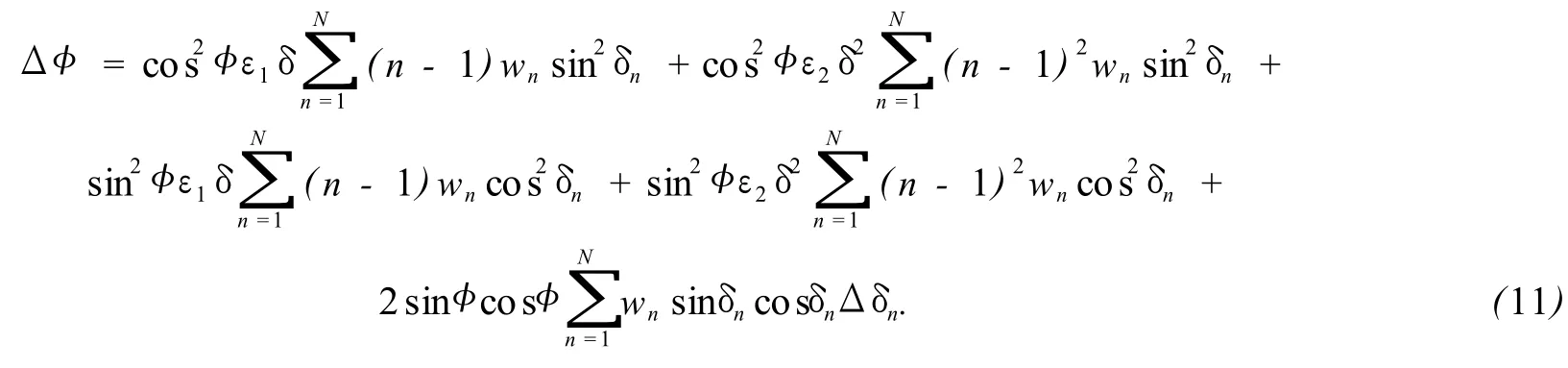
要实现算法对 PZT的移相不准不敏感,需要满足约束条件:

2.2 CCD响应非线性
在探测器获取干涉图的过程中存在非线性响应误差,这种误差是由于探测器的输出信号与入射的干涉图光强信号之间的响应非线性引起的。由于移相算法提取相位时,每个像素点的相位提取与其他点无关,所以对 CCD响应非均匀性的要求不高[12]。当仅仅存在二阶非线性响应误差时,探测器输出的干涉图信号与干涉图光强信号之间的关系以及响应ΔIn偏差可表示为[13]:
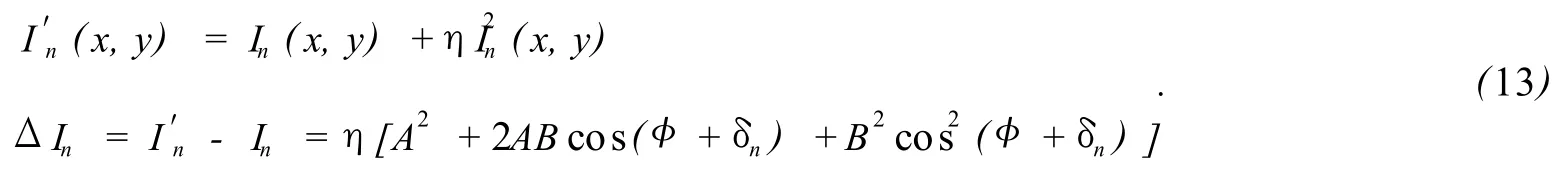
仅仅存在 CCD的二阶响应非线性时,可得到相位误差Δφ:

要实现算法对探测器的二阶非线性误差不敏感,需要满足的约束条件如下:

2.3 光源的不稳定性
光源的不稳定性可分为光强不稳定性和频率不稳定性。前者使得干涉图的背景光强和调制光强发生变化;后者引入额外相位差,造成移相不准。
2.3.1 光源的光强不稳定
光强不稳定性包括短周期的光强噪声和长周期的光强波动。当存在光强的长期波动时,干涉图可以用帧数的多项式表示,因此第n帧干涉图以及探测器输出的干涉图信号与理想干涉图光强信号之间的偏差可分别表示为[13]:

仅仅存在光强波动时,可得到相位误差Δφ为:

要实现算法对光源的一阶和二阶光强波动不敏感,需要满足如下一组约束条件
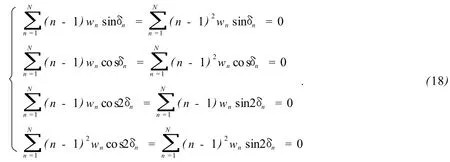
当存在光强的短期噪声αn时,干涉图可以表示为:
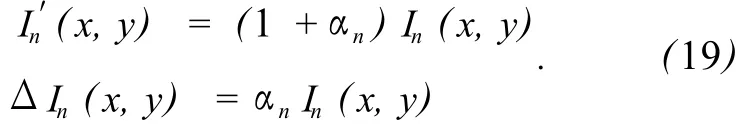
同样处理,要实现算法对光源的一阶和二阶光强波动不敏感,需要满足一组约束条件:
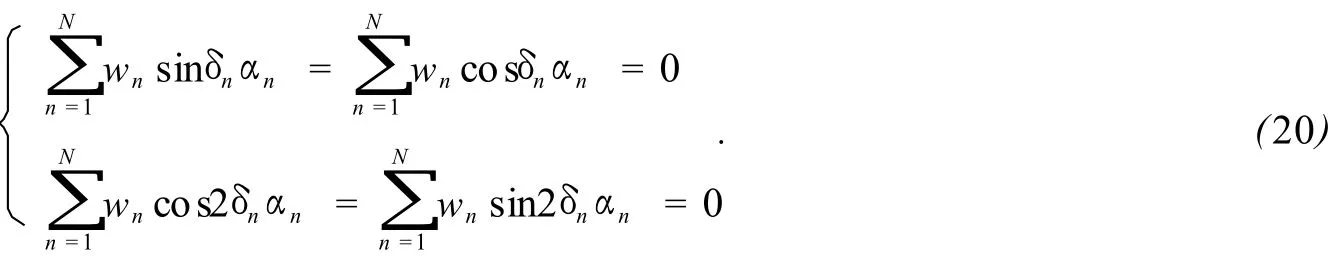
由于αn为一个随机量,式 (23)不能在αn为任意值时都满足。
2.3.2 光源的频率不稳定
激光器的频率不稳定性可分为长期的频率波动和短期的频率噪声。由频率与波长之间的相互关系可知,不同时刻激光器的中心波长不同,这样会改变干涉图的相位,从而造成了一种移相不准。当仅仅存在激光器的频率波动时,引入的额外相位差为:

这种移相不准与激光器的频率波动大小成正比。当仅仅存在长期波动时,频率可用帧数的多项式表示为:
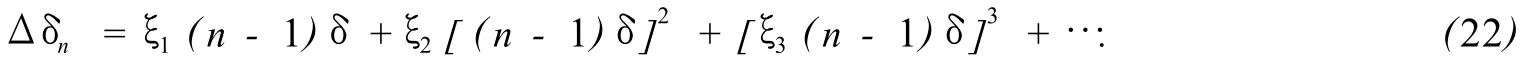
上式与前面的 PZT的线性和非线性移相不 准形式一致,为了消除光源频率的一阶和二阶波动,需要满足式 (12)。
当仅仅存在光源频率的短期噪声时,相位提取误差可表示为:

要实现算法对频率噪声不敏感,需要满足如下约束条件:
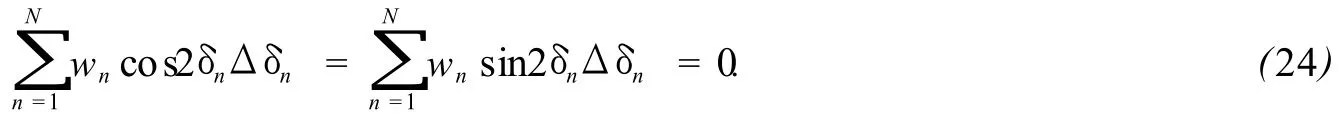
由于 Δ δn为一个随机量 ,式 (23)不能在 Δ δn为任意值时都满足。
2.4 加权最小二乘算法获取
综合考虑上面 2.1,2.2和 2.3节中的分析,要使得算法对 PZT的移相不准、CCD的二阶响应非线性和光源的不稳定性不敏感,需要满足如下条件:
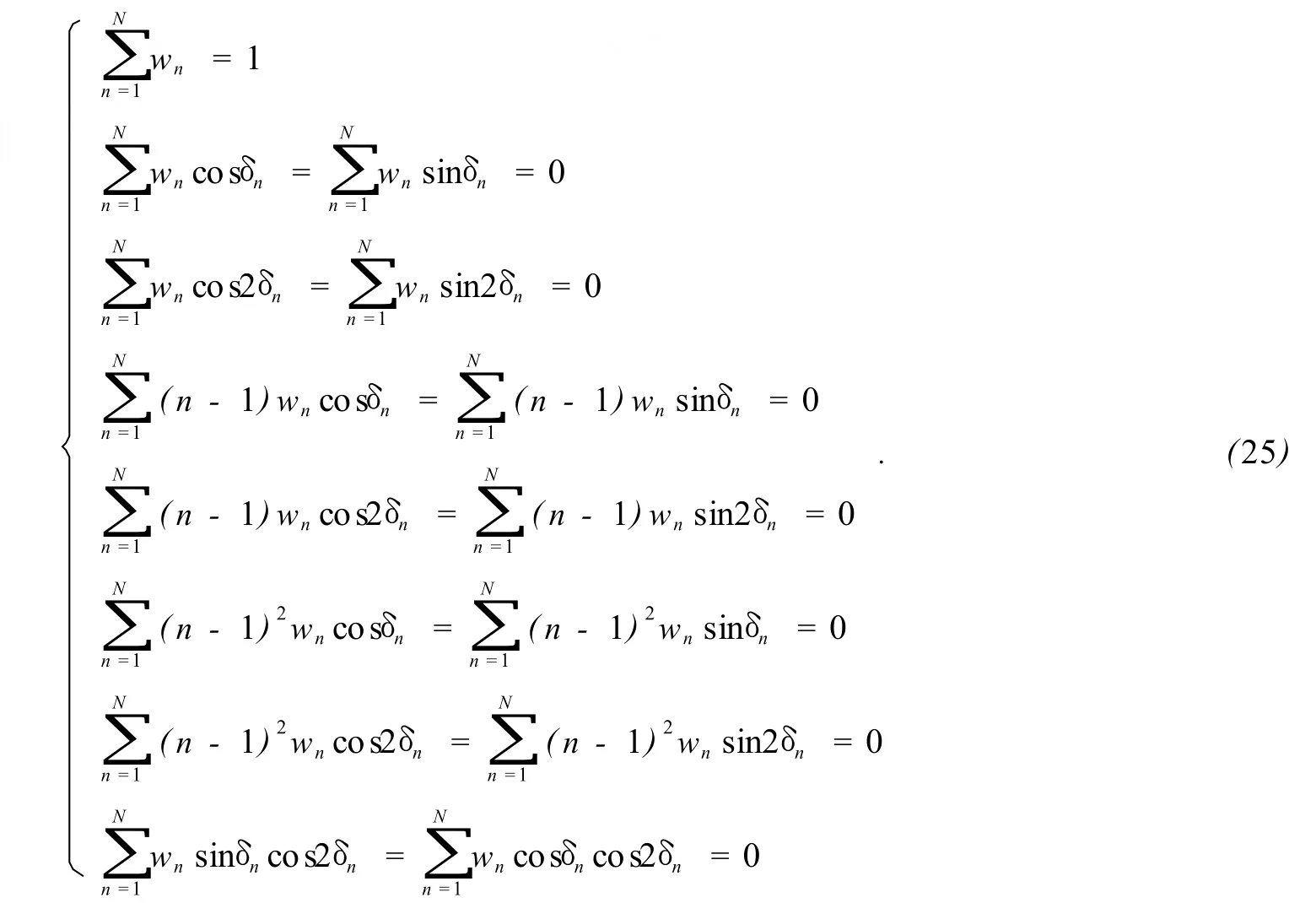
为方便分析,设定权重为正实数且对称分布,对于移相量为π/2的等间隔多步移相,上述方程组共有 12个方程,假设移相步数为 13,求解方程组获得权重如下:

3 对比仿真
仿真生成待测面形和干涉图分别如图1(a)和图1(b)所示,待测面形 PV=4.705 nm;RMS=1.007 nm。下面分别对 PZT的移相不准、CCD的二阶响应非线性和光源的不稳定性做比对分析。

图1 仿真图Fig.1 Simulating pictures
3.1 PZT移相不准对比仿真
当存在 PZT的移相不准时,对比仿真结果如图2所示。图2中的误差为与相位提取误差值对应的面形检测误差值,下面仿真中的误差值也是如此。
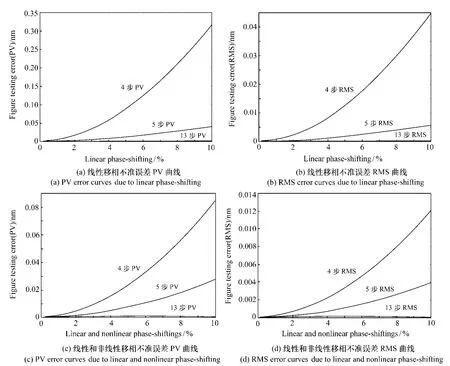
图2 移相不准引起的检测误差Fig.2 Testing errors due to phase-shifting errors
图2(a)和图2(b)分别为线性移相不准从0%变化到 10%时的面形检测误差 PV曲线和RMS曲线;图2(c)和图2(d)分别为线性和二阶非线性移相不准从 0%变化到 10%时的处理误差PV曲线和 RMS曲线。明显新算法抑制 PZT的线性和二阶非线性移相不准误差的能力远远优于其他两种算法。
3.2 CCD响应非线性和量化误差对比仿真
当存在 CCD的二阶响应非线性,对比仿真结果如图3所示,图3(a)和图3(b)分别为 CCD二阶响应非线性从 0%变化到 10%时的面形检测误差 PV曲线和 RMS曲线。明显三种算法对于CCD的二阶响应非线性完全不敏感。
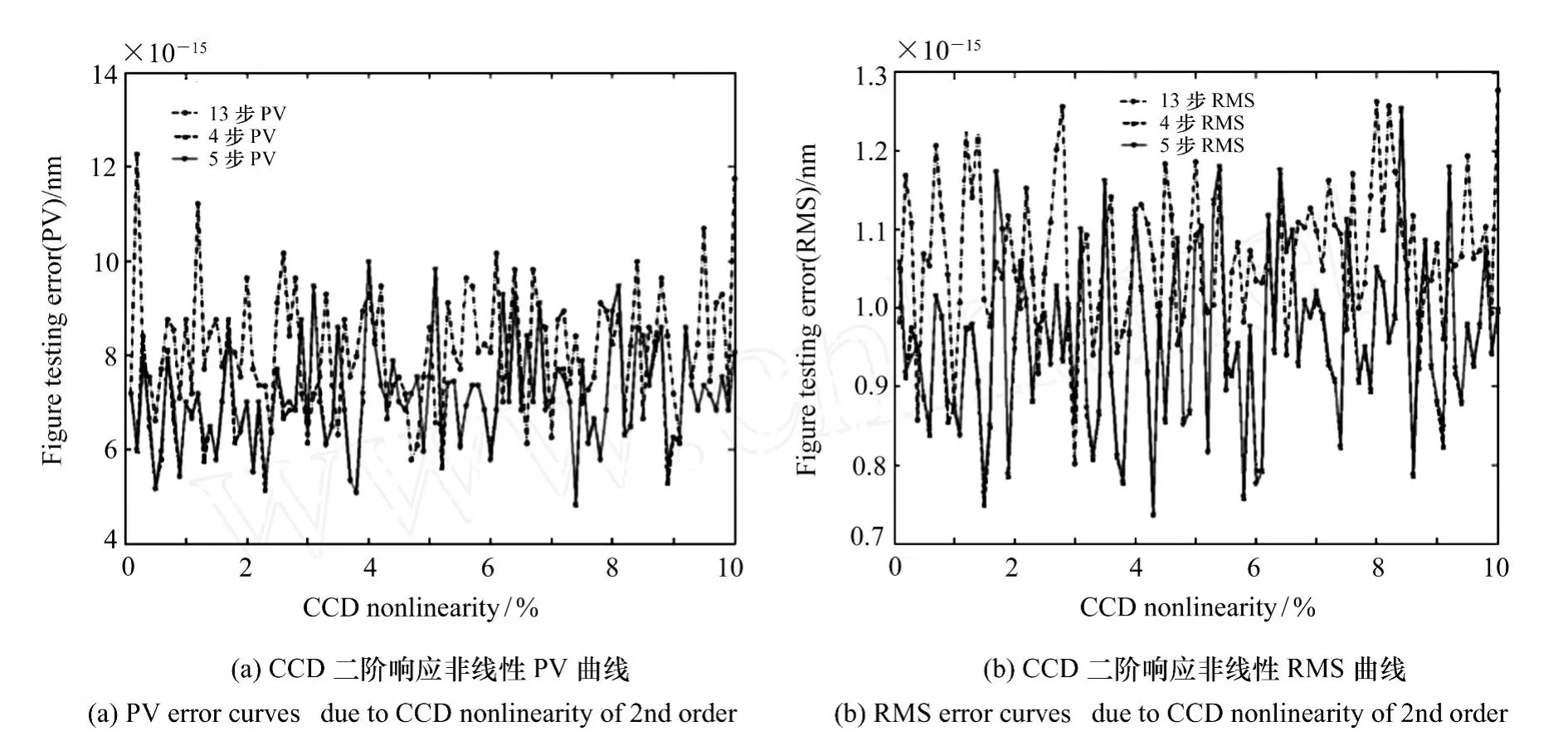
图3 CCD的二阶响应非线性引入的检测误差Fig.3 Testing errors due to CCD nonlinearity of 2nd order
根据 C.P.Brophy的研究结果[14],当干涉条纹的对比度分别为 0.8和 1时,面形检测误差与量化深度之间的曲线如图4所示。图4中新算法对探测器的量化误差抑制能力比四步算法、五步算法更强。
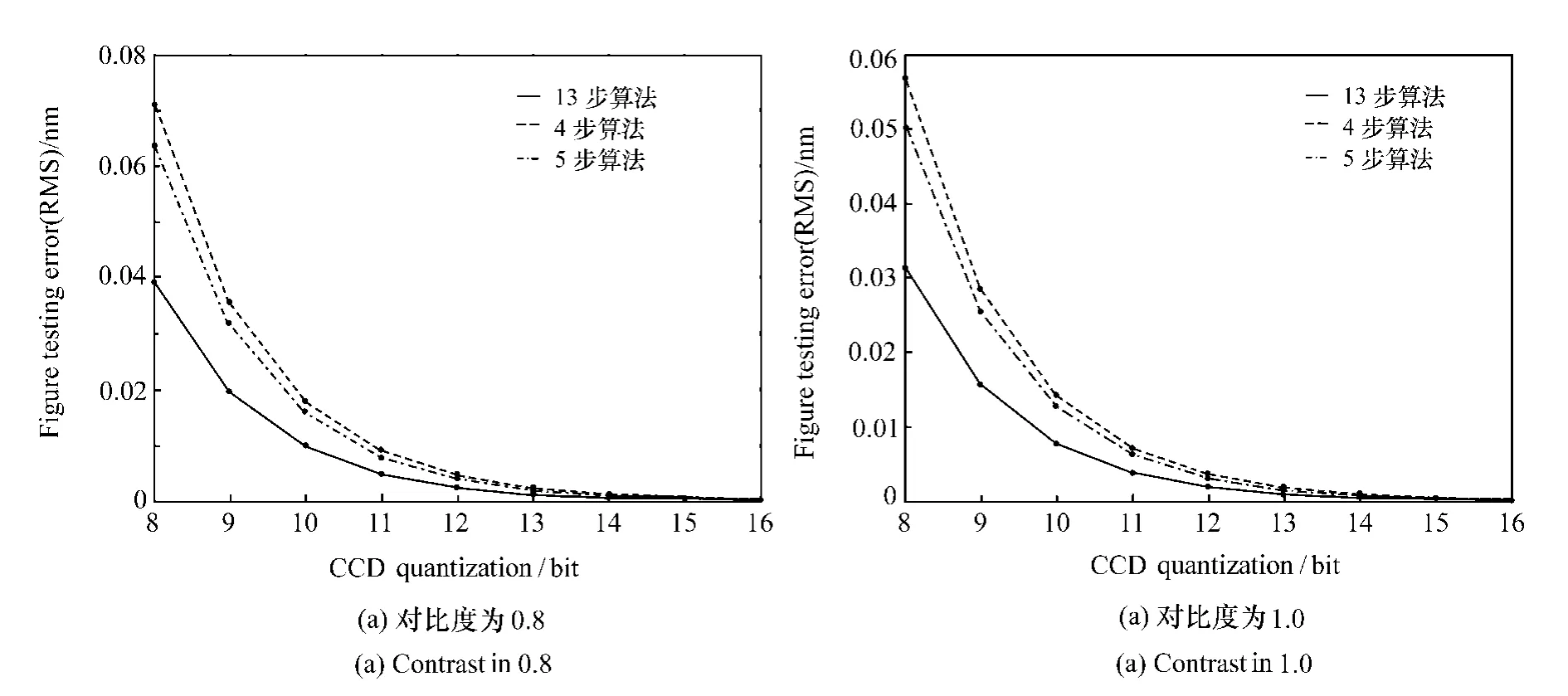
图4 CCD量化误差引入的检测误差Fig.4 Testing errors due to CCD quantization
3.3 光源不稳定性对比仿真
当存在光源的光强不稳定性时,对比仿真结果如图5所示。图5(a)和图5(b)分别为光源的功率波动幅度从 0.5%变化到 50%时的面形检测误差 PV曲线和 RMS曲线;图5(c)和图5(d)分别为光源的长期功率波动的幅度为 5%,短期功率噪声幅度为 ±2%时的面形检测误差 PV曲线和 RMS曲线。明显新算法抑制光源的一阶二阶光强波动影响的能力远远优于其他两种算法。从图5中可得,新算法对于光强噪声的抑制能力也优于其他两种算法。

图5 光强不稳定性引起的检测误差Fig.5 Testing errors due to intensity instability
当存在光源的频率不稳定性时,对比仿真结果如图6所示。图6(a)和图6(b)分别为频率波动从 ±0.1 MHz变化到 ±10 MHz时的面形检测误差 PV曲线和 RMS曲线;图6(c)和图6(d)分别为频率噪声大小为 ±2 MHz,频率波动从±0.1 MHz变化到 ±10 MHz时的面形检测误差PV曲线和 RMS曲线。图6中可得,新算法抑制光源的一阶二阶频率波动影响的能力远远优于其他两种算法。新算法对于频率噪声的抑制能力也优于其他两种算法。

图6 频率不稳定性引入的检测误差Fig.6 Testing errors due to frequency instability
4 结 论
本文首先利用权重待定的方法,通过分析多种误差对等间隔多步移相算法的影响得到多组约束条件,联立多组约束条件进而确定权重,从而得到对多种误差不敏感的新算法。其次,利用新算法、四步算法以及 Hariharan五步算法进行比对仿真。仿真结果验证了新算法抑制 PZT线性和二阶非线性移相不准、光强的一阶和二阶波动、光源频率的一阶和二阶波动等误差的能力远远优于四步算法和 Hariharan五步算法。同时,新算法抑制 CCD的量化误差、光强噪声、光源频率噪声的能力也要优于其他两种算法,且新算法与其他两种算法对于 CCD的二阶响应非线性完全不敏感。结果显示,新算法能满足检测精度达到 0.1 nm的超高精度面形检测的要求。
[1] BRUN ING J H,SCHRE IBER H.Optical Shop Testing[M].3rd edition.Hoboken:A JohnW iley&Sons,2007.
[2] BRUN ING J H,HERR IOTT D J,BALLAGHER J E,et al..Digital wavefront measuring interferometer for testing optical surface and lenss[J].Appl.Opt.,1974,13(11):2693-2703.
[3] SOMMARGREN G E.Phase shifting diffraction interferometry formeasure extreme ultravioletoptics[J].OSA TrendsOpt.Photonics,1999,4:108-112.
[4] NOVAK J.Five-step phase-shifting algorithms with unknown values of phase shift[J].Optik,2003,2(114):63-68.
[5] NOVAKJ,NOVAK P,M IKSA.Multi-step phase-shifting algorithms insensitive to linearphase shift errors[J].Opt.Comm unications,2008,281:5302-5309.
[6] TANG SH H.Generalized algorithm for phase shifting interferometry[J].SPIE,1996,2860:34-44.
[7] CA IL Z,L IU Q,YANG X L.Phase-shift extraction and wave-front reconstruction in phase-shifting interferometrywith arbitrary phase steps[J].Opt.Lett.,2003,28(19):1808-1810.
[8] CA IL Z,L IU Q,YANG X L.Generalized phase-shifting interferometry with arbitrary unknown phase steps for diffraction objects[J].Opt.Lett.,2004,29(2):183-185.
[9] CREATH K.Error sources in phase-measuring interferometry[J].SPIE,1992,1720:428-435.
[10] HAR I HARAN P,OREB B F,EIJU T.Digitalphase-shifting interferometry:a simple error-compensating phase calculation algorithm[J].Appl.Opt.,1987,26(13):2504-2506.
[11] SCHW IDER J,BUROW R,ELSSNER K-E,et al..Digital wave-front measuring interferometry:some systematic error sources[J].Appl.Opt.,1983,22(21):3421-3432.
[12] 程万杰,赵杰,蔡鹤皋.CCD像素响应非均匀的校正方法[J].光学精密工程,2008,16(2):314-318.CHENGW J,ZHAO J,CA IH G.Correctionmethod for pixel response nonuniformity of CCD[J].Opt.Precision Eng.,2008,16(2):314-318.(in Chinese)
[13] PH ILL ION D W.General methods for generating phase-shifting interferometry algorithms[J].Appl.Opt.,1997,36(31):8098-8115.
[14] BROPHY P.Effect of intensity error correlation on the computed phase of phase-shifting interferometry[J].Opt.Soc.Am.A,1990,7(4):537-541.
