计及调速器死区影响的两区域互联电力系统AGC研究

温步瀛

（福州大学电气工程与自动化学院 福州 350108）

计及调速器死区影响的两区域互联电力系统AGC研究

温步瀛

（福州大学电气工程与自动化学院 福州 350108）

自动发电控制在电力系统运行中是十分重要的。但为了减少调速器的频繁动作而设置调节死区，从而增加了控制系统的复杂性。本文利用非线性系统中的描述函数法将调速器死区进行线性化，建立了计及调速器死区特性影响的两区域互联电力系统自动发电控制的仿真模型，并采用改进的粒子群优化算法对其积分参数和区域频率偏差系数进行寻优。通过对两区域互联电力系统自动发电控制系统的仿真分析，结果表明新建模型更能真实反映自动发电控制调节过程的动态性能，同时也说明了该处理方法的合理性。

描述函数 调速器死区 自动发电控制 粒子群优化

1 引言

自动发电控制(Automatic Generation Control，AGC)是频率二次调整的自动实现方式，其目的是通过调节各发电机出力，使不同区域电网之间的负荷和发电功率之间保持平衡。为了减少调速系统控制器的频繁动作，发电机组的一次调频控制回路中需要设置调频死区。当在一次回路设置调频死区时，就会在电力系统中引入强非线性环节，因此增加了AGC控制系统的复杂性。

近年来对电力系统AGC相关问题的研究很活跃[1-10]，文献[1]研究了主调频水电站频率调整的辨识模型和频率预报模型，文献[2]探讨了火电机组 AGC的动态特性及其优化控制策略，文献[3]建立了定量计算 AGC系统中时滞信号的时滞极限模型，文献[4]探讨了互联电网CPS标准下提高电网频率质量的 AGC控制的一些策略，文献[5]初步探讨了多区域电力系统的有功频率控制问题及改善系统的频率特性方法，文献[6-7]探讨了采用传统的比例积分控制系统和模糊逻辑控制系统的水火互联系统的 AGC问题。文献[8]采用现场调试参数的方法来考虑非线性的影响，但所期望的性能还需要提高。文献[9]建立了三区域系统的数学模型，对机组参与电网一次调频特性进行了系统分析，给出了机组调频死区与一次调频容量以及负荷扰动之间的关系，然而如何考虑调速器死区对控制器参数选择的影响还需要进一步分析。文献[10]论述了考虑调频死区影响的AGC控制回路的设计，利用Popov稳定判据选择PI控制器参数，并讨论了 AGC控制回路中 PI参数的变化对系统频率控制质量的影响，然而对参数的优化选择方面也需要进一步的研究。综上所述，目前对 AGC相关问题的研究虽然取得了一定的成果，但是由于AGC问题的复杂性，很多方面的问题仍然还需要进一步的研究[11]。

本文是在借鉴上述文献的基础上，利用描述函数法将调速死区线性化，建立了计及调速器死区特性的两区域互联电力系统 AGC的数学仿真模型，并利用改进的粒子群优化算法对控制器的积分增益和区域频率偏差系数进行寻优。

2 调速器死区数学模型的建立

2.1 调速器死区的非线性问题

在发电机组的 AGC中引入了非线性环节，则对 AGC的动态响应有很大的影响。一般死区是具有滞后型的非线性问题，可用间隙特性进行描述，如图1所示。

图1 死区特性Fig.1 Dead band characteristic

调速器死区输入与输出的关系描述为

对于一个非线性元件，如果对应于非线性环节的输入信号为正弦信号即式（2）时，只需考虑输出中的基波分量时，则可用描述函数法将线性化。

式中 A——正弦输入信号幅值；

ω0——正弦输入信号频率。

2.2 调速器死区的描述函数

描述函数法是用来在无外加作用的条件下分析非线性系统稳定性的一种方法。描述函数法已应用于导弹制导控制系统中非线性环节的设计和电液位置系统中进行频域分析，并收到了较好的效果[12-13]。本文将利用描述函数法对电力系统 AGC问题的调速死区进行线性化研究。当给非线性环节一个正弦信号输入时，其输出仍是一个周期与输入信号相同的信号，由基波和高次谐波组成。由于在许多情况下信号通过系统后，相对于基波来说，高次谐波被衰减了许多。可以假设对系统性能起决定意义的仅仅是非线性环节输出的基波分量，在分析中可忽略其他高次谐波分量的影响。为此非线性环节输出的一次谐波（即基波）分量对输入正弦信号幅值之比作为该环节的描述函数。

非线性函数 F(X,X.)中X具有正弦形式，所以可用傅里叶级数将非线性函数 F(X,X.)展开，并仅取前三项得

式中

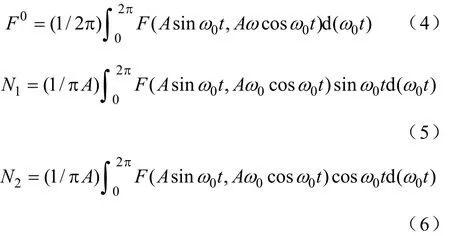
经过对上式的积分可得各系数满足下列关系：

式中 h——调速器死区设定值，如图1所示。A的意义与式（2）相同。

当 k=1时，死区傅里叶级数展开系数 N1、N2随A/h的变化关系如图2和图3所示。

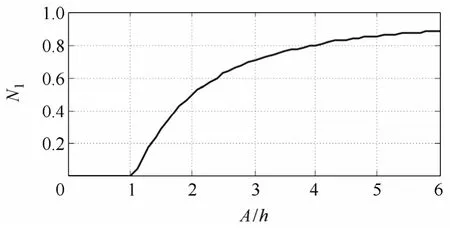
图2 傅里叶级数展开线性项系数N1变化趋势Fig.2 The change trend of Fourier series linear coefficient of N1

图3 傅里叶级数展开非线性项系数N2变化趋势Fig.3 The change trend of Fourier series nonlinear coefficient of N2

从图2、图3可知：

（1）当A=h时，N1=0，N2=0。

（2）当A/h增大时，N1是单调增加；而N2下降至A/h=2后也是递增的。

（3）当A/h→∞时，N1、N2趋于常数。

对于汽轮机调速器模型，将式（7）代入式（3）且将其进行拉普拉斯变换可得线性化后计及死区的调速器传递函数为

式中 TGi——调速器的时间常数；

αi——傅里叶级数展开线性项系数，αi=N1；

βi——傅里叶级数展开非线性项系数，βi=N2/ω。

AGC通过一个闭环控制系统实现，一般 AGC的启动周期为 4s，每 2s向机组或电厂发送一个控制指令值，即 ω0= 2πf0= 2π×0. 5 = π。对于图1所示的间隙特性，当A/h=4时，相当于调速器的死区设置为 0.03Hz。当 A/h=4，由图 2和图 3可知此时N1=0.8，N2=−0.24。

3 计及调速器死区的AGC状态方程的描述

按照 AGC仿真的建模思想可以建立计及调速器死区特性的两区域火电互联电力系统 AGC调节仿真模型如图4所示。

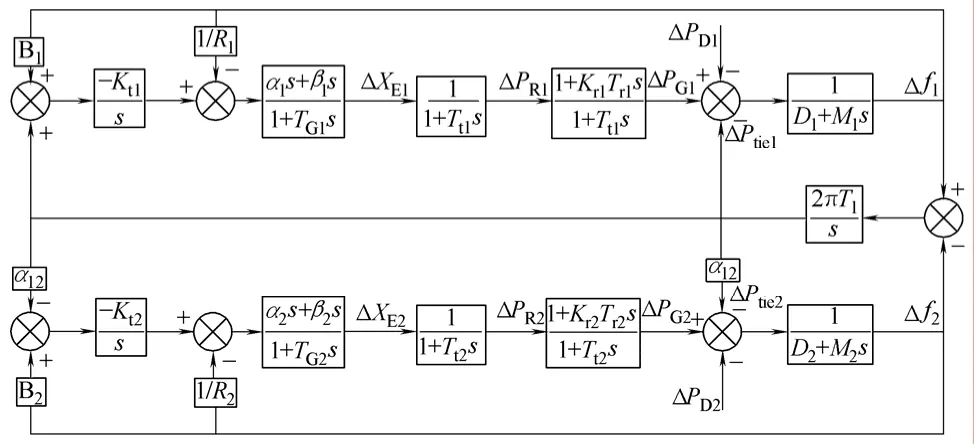
图4 计及调速器死区的两区域互联系统AGC调节Fig.4 Two-area power system for AGC regulation considering governor dead band

对调速器部分，计及其死区的非线性问题后则有

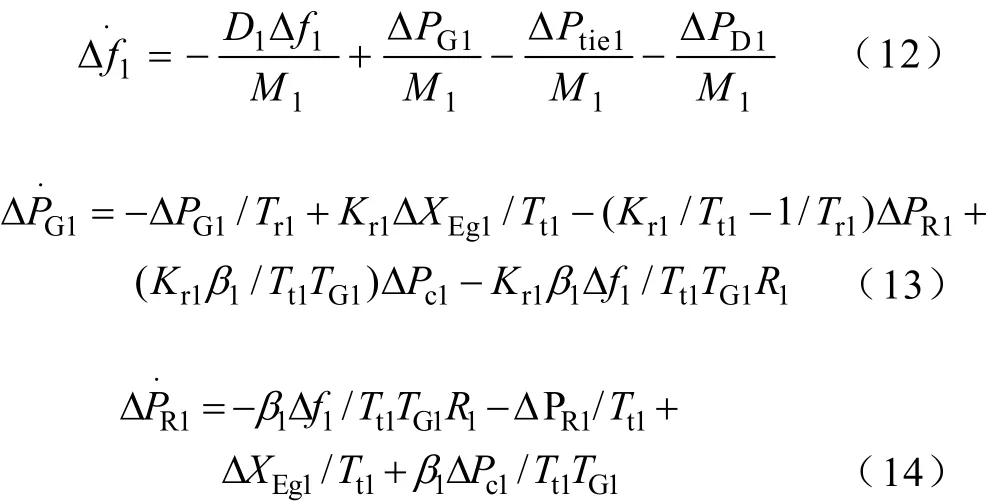
式（9）～式（22）中，T12为联络线的同步系数；Tr1是再热器时间常数；其他参数意义详见文献[5]。

4 采用改进的粒子群算法优化两区域系统的AGC参数

4.1 基本粒子群优化算法

粒子群优化(Particle Swarm Optimization，PSO)算法是一种基于群体智能的进化算法，PSO算法中的每个粒子通过统计迭代过程中自身的最优值和群体最优值不断地修正自己的前进方向和速度的大小。

粒子群优化算法的基本思路是：首先，PSO算法初始化产生m×n维随机粒子（对应m×n维随机解），粒子（ i∈ (1,2,⋅⋅,m )）的位置和速度分别为且每个粒子的优劣由具有与优化目标函数相关的适应值来表示；然后粒子通过追踪两个极值来更新。第一个就是粒子本身所找到的最优解，叫做个体极值pbest；另一个极值是整个种群目前找到的最优解，即全局最优解gbest。粒子群优化算法可用以下两个等式来表示：

式中，r1、r2是介于（0，1）之间的随机数；c1、c2是学习因子；Pid为pbest；上标k为迭代次数。

4.2 改进的粒子群优化算法

从粒子群优化算法的应用及仿真中可以看到，粒子群算法的各个参数与收敛速度和精度的关系，粒子数目越多、搜索范围越小和合理的速度调整范围都会使算法收敛得更快、精度更高。由于电力系统 AGC控制模型的仿真运算及估值函数的计算工作量很大，粒子数和迭代次数需要控制。但这两方面的要求又相互矛盾，为此采用改进的粒子群优化算法[14-15]。其主要思路是：在每个粒子速度更新的过程中随机产生r1、r2、r3、r4，平衡每个粒子的认知和粒子间的社会信息交换能力，以扩展粒子的搜索空间能力；通过sign(r3)、sign(r4)、Pcraz、vcrazinessi来指引粒子更新的方向和调整速度更新的大小，以防止当前值陷入局部最优值和提高整个群体的收敛速度。

按照以上思路，改进后粒子群优化算法速度的更新可用下式表示：

式中，r1、r2是介于（0，1）之间的随机数；r3、r4是介于（0，1）之间的随机数；是介于[0.1,0.4]之间的随机数。仿真时取为0.3，Pcraz＝0.2。

4.3 改进的粒子群算法优化两区域系统AGC参数的实施技术

对于两区域互联电力系统来说，控制目标是使区域内的频率变化量Δf尽快地被调整为零，而使Δf变为零的控制量为 ACE，因此选择ACE的平方积分标准来优化积分系数和区域频率偏差系数，适应度函数可以表示为式（30）。其主要的约束条件为发电机的调节速率以及单个区域内AGC容量的约束。

根据两区域互联系统的模型可知，需优化的参数为积分系数和区域频率偏差系数Bi。用改进的粒子群算法优化两区域电力系统参数的步骤如下：

（1）确定Kti与Bi的范围，随机产生一定种群规模粒子的位置和速度。

（2）运用Kti与Bi的初始值，结合变步长的龙格库塔法对系统进行仿真，根据适应度函数计算该粒子的适应值；判断是否达到仿真时间，如否，则继续对系统仿真，否则转入下一步。

（3）对每个微粒，将其适应值与其经过的最好位置pbest作比较，如果较好，则将其作为pbest。

（4）对每个微粒，将其适应值与其经过的最好位置gbest作比较，如果较好，则将其作为gbest。

（5）根据式(25)、式(26)调整微粒速度和位置。

（6）如果迭代次数未到达设定的次数，或适应值误差小于设定误差限，则输出结果；否则转向（2）。

5 算例分析

为了探讨计及调速器死区影响的两区域火电互联电力系统AGC的动态响应性能，并利用上述改进的粒子群优化算法来进行 AGC参数优化。设种群规模为30，迭代次数为 50，系统仿真时间为 40s，且各区域电力系统的参数与文献[5]相同。当区域1发生1%的负荷扰动时，得到的适应度收敛特性曲线和两区域系统AGC调节的动态响应特性分别如图5和图6所示。

图5 粒子群优化适应度收敛曲线Fig.5 Fitness function convergence curve using PSO algorithm

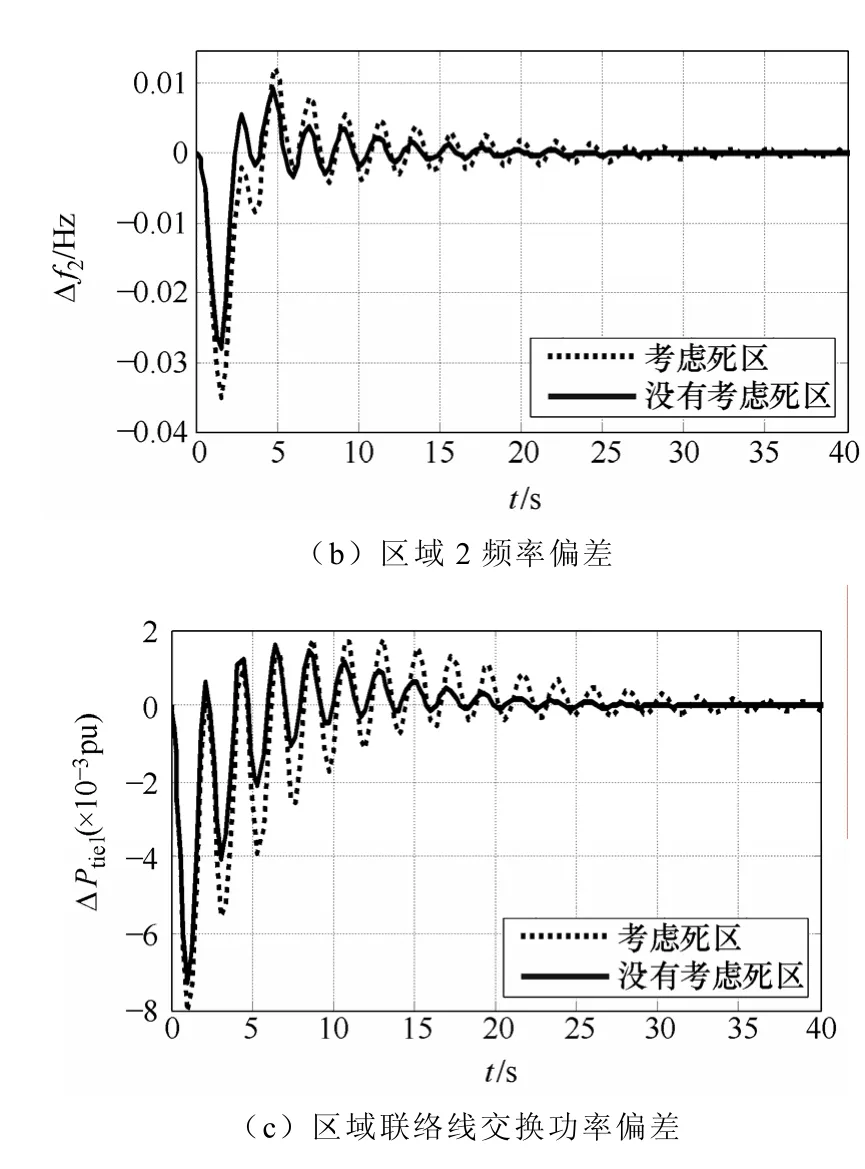
图6 两区域互联AGC调节动态响应Fig. 6 Dynamic response of two area power systems for AGC regulation

从两区域动态响应的结果可知：

（1）在不考虑调速器死区的情况下，两区域电力系统的动态响应较理想化，波动幅度较小。

（2）考虑调速器死区时，系统的动态响应波动幅度较大，特别是在负荷扰动初期，系统频率出现了较大的超调，但结果更接近实际情况。

（3）考虑调速器死区时，系统的稳定时间较长，大约需要40s过后，且以连续的正弦波动趋于稳定。

本文还将粒子群算法优化的结果与遗传算法优化的结果进行了比较。在两种算法的仿真比较中，取相同的估值函数与种群数目，对系统仿真后得到区域交换功率偏差动态响应如图7所示。

图7 区域联络线交换功率偏差Fig.7 Tie line power flow deviation for a 0.01(pu) step load change

从图中可以看出，用改进的粒子群算法优化后系统的阶跃响应曲线的特性与遗传算法的优化结果相比有着更好的特性。仿真的过程也表明，在使用改进的粒子群算法优化的过程中，参数的收敛速度和精度也高于遗传算法。

6 结论

本文采用描述函数对电力系统 AGC的调速器死区进行了线性化描述，推导了计及调速器死区特性的两区域互联电力系统 AGC调节的数学模型，并利用改进的粒子群优化算法对其积分参数和区域频率偏差系数进行寻优，以及采用两区域互联电力系统的实例进行了仿真分析。结果表明考虑调速器死区特性后，系统的动态响应波动较大，且稳定时间较长。

[1] 张明锐, 王为. 电力系统短期预报频率控制[J]. 电工技术学报, 2002, 17(1): 96-100. Zhang Mingrui, Wang Wei. Short term frequency forecasting control for electric power system[J]. Transactions of China Electrotechnical Society, 2002, 17(1): 96-100.

[2] 周罡, 吕剑虹, 韦红旗, 等. 自动发电控制优化控制策略研究与应用[J]. 中国电力, 2004, 37(1): 57- 61. Zhou Gang, Lü Jianhong, Wei Hongqi, et al. Study and application of optimal control strategy for automatic generating control[J]. Electric Power, 2004, 37(1): 57-61.

[3] 刘梅招, 杨莉, 甘德强, 等. 存在均匀通信时滞的AGC稳定极限计算[J]. 电力系统自动化, 2006, 30 (19): 7-12. Liu Mei Zhao, Yang Li, Gan Deqiang, et al. Computing the delay margin of AGC system with commensurate communication delay[J]. Automation of Electric Power Systems, 2006, 30(19): 7-12.

[4] 高宗和, 滕贤亮, 张小白. 互联电网 CPS标准下的自动发电控制策略[J]. 电力系统自动化, 2005, 29 (19): 40-44. Gao Zhonghe, Teng Xianliang, Zhang Xiaobai. Automatic generation control strategy under control performance standard for interconneted power grid[J]. Automation of Electric Power Systems, 2005, 29(19): 40-44.

[5] Olie I Elgerd, Charles E Fosha. Optimum megawattfrequency control of multi-area electric energy system [J]. IEEE Trans. Power Apparatus Syst, 1970, 89 (4): 556-563.

[6] Janardan Nanda, Ashish Mangla, Sanjay Suri. Some new findings on automatic generation control of an interconnected hydrothermal system with conventional controllers[J]. IEEE Transactions on Energy Conversion, 2006, 21(1): 187-194.

[7] Janardan Nanda, Ashish Mangla. Automatic generation control of an interconnected hydro-thermal system using conventional integral and fuzzy logic controller[C]. IEEE International Conference Electric Utility Deregulation, Restructuring and Power Technologies, Hong Kong, April 2004, 1: 372- 377.

[8] 李平康. 火电厂 AGC及其可视化仿真实现[J]. 华北电力技术, 2000(10): 10-13. Li Pingkang. Automatic generation control and its visualized simulation for coal-fired power plant[J]. North China Electric Power, 2000(10): 10-13.

[9] 戴义平, 赵婷, 高林. 发电机组参与电网一次调频的特性研究[J]. 中国电力, 2006, 39(11): 37-41. Dai Yiping, Zhao Ting, Gao Lin. Research on characteristics of power system primary frequency control operating on power plants[J]. Electric Power, 2006, 39(11): 37-41.

[10] 郭钰锋, 徐志强, 于达仁, 等. 考虑调频死区的二次调频控制回路设计[J]. 中国电机工程学报, 2004, 24(10): 77-81. Guo Yufeng, Xu Zhiqiang, Yu Daren, et al. The design of secondary frequency regulation loop considering regulation dead band[J]. Proceedings of the CSEE, 2004, 24(10): 77-81.

[11] 刘梦欣, 王杰, 陈陈. 电力系统频率控制理论与发展[J]. 电工技术学报, 2007, 22(11): 135-144. Liu Mengxin, Wang Jie, Chen Chen. Theory and development of power system frequency control[J]. Transactions of China Electrotechnical Society, 2007, 22(11): 135-144.

[12] 沈浩, 夏群力, 祁载康, 等. 速度追踪制导控制系统描述函数法设计[J]. 北京理工大学学报, 2007, 27 (7): 590-593. Shen Hao, Xia Qunli, Qi Zaikang, et al. Design the description function of guidance system with velocity pursuit guidance law[J]. Tansactions of BeijingInstitute of Technology, 2007, 27(7): 590-593.

[13] 曾宗桢, 张小安, 肖飞. 电液位置系统的非线性校正与描述函数法分析[J]. 机床与液压, 2005(10): 110-112. Zeng Zongzhen, Zhang Xiaoan, Xiao Fei. Nonlinear regulation of electric hydraulic position system and analysis with described function[J]. Machine Tool and Hydraulic Pressure, 2005(10): 110-112.

[14] Mukherjee V, Ghoshal S P. Comparison of intelligent fuzzy based AGC coordinated PID controlled and PSS controlled AVR system[J]. Electric Power and Energy Systems, 2007, 29(3): 679-689.

[15] Shayeghi H, Jalili A, Shayanfar H A. Multi-stage fuzzy load frequency control using PSO[J]. Energy Conversion and Management, 2008, 49(10): 2570-2580.

Research on AGC of Two-Area Interconnected Power System Considering the Effect of the Governor Dead Band

Wen Buying
（Fuzhou University Fuzhou 350108 China）

Automatic generation control (AGC) is very important to power system operation. But for reducing its action number, it should be set a dead band for governor，as a result to increase its complexity. In this paper a new simulation model considering the effect of governor dead band nonlinearity by using the describing function approach for automatic generation control studies of two-area system is proposed. And an improvement particle swarm optimization algorithm used to optimum the parameters of the integral controller and area frequency deviation coefficient. Through the simulation analysis of the automatic generation control system of two-area interconnected power system, the results show that the new proposed model can actually enough to express the performances of the automatic generation control system, and that this method is effective.

Describing function, governor dead band, automatic generation control, particle swarm optimization

TM761

温步瀛 男，1967年生，博士，教授，主要研究方向为电力系统优化运行、电力市场和风电并网运行技术。

福建省自然科学基金资助项目（2008J0018）。

2008-11-11 改稿日期 2009-06-16