基于椭圆曲线的一种盲数字签名设计

谢 扬 ，王金凤

（1.重庆大学 通信工程学院，重庆400044；2.重庆电子工程职业学院 软件工程系，重庆401331）

基于椭圆曲线的一种盲数字签名设计

谢 扬1，王金凤2

（1.重庆大学 通信工程学院，重庆400044；2.重庆电子工程职业学院 软件工程系，重庆401331）

随着计算机和通信技术的迅速发展，对信息的保密性与真实性的要求越来越高。公钥密码体制的出现是为了解决对称密钥所不能解决的问题，而数字签名是公钥密码的一个重要的应用。数字签名在信息安全技术中的身份认证、数据完整性、不可否认性及匿名性等方面起到了重要的作用，本文基于椭圆曲线密码体制的盲数字签名设计，并分析了其安全性，对建立一个安全有效的电子认证系统有一定现实价值。

椭圆曲线；盲数字签名；协议安全

1 引言

随着计算机和通信技术的迅速发展，大量的敏感信息常常通过公共通讯设施或计算机网络进行交换，越来越多的个人信息需要得到严格保密。公钥密钥密码是现代密码学中最重要的研究内容之一，它不但能为在网络中传递的信息提供机密性的保护，而且还能提供信息的发送人的身份认证以及信息的完整性检验。

公钥密码仍存在一些缺点：因为公钥密码的计算是对大数进行操作，不同于对称密码是对比特位进行操作，因而它的计算量较大。因此，在网络上都用公钥密码来加密机密文件是一件花销很大的事。我们可以利用公开密钥的特性，只把它用于对对称密钥进行加密，而用对称密钥来加密文件，这样的方法称之为数字信封。这样既解决了密钥协商的问题，又弥补了公钥加密速度慢的不足。

2 公钥密码体制的实现基础

公钥密码体制的成功依赖于这样一个问题：怎样才能实现由 Ei（加密）获得 Di（解密）,即求 Ei-1是困难的。可通过单向函数实现这样的要求。严格单向函数：

对一个单向函数f：X→Y，如果下述条件成立：存在一个有效的方法，对所有的x∈X可计算f(x),但是不存在有效的方法由y＝f(x)计算x，对所有的y∈f[X]。则称函数f：X→Y是严格单向函数。

严格的加密函数由于不能反向计算，所以不能用于消息的加密和解密，但是却可以用于数字签名和身份的认证识别。

陷门单向函数：

只允许合法的用户通过解密访问数据，对于单射函数f：X→Y，如果满足对所有x∈X，存在一个有效的方法计算f(x)，而且对所有y∈f[X]，存在一个有效方法计算f-1(y)，但是对所有y∈f[X]不能从关系式y＝f(x)有效地导出f-1(y)：这需要额外的秘密信息，即陷门。则单射函数f：X→Y为陷门单向函数。

3 公钥密码体制的设计

设计公钥密码体制首先要寻找一个单向陷门函数，在数学中称为NP问题或NPC问题，NP问题是指在非确定性图灵机上可用多项式时间求解的问题，称为非确定性多项式时间可解问题。在NP类问题中困难程度最大的一类问题称为NP完全类，即NPC问题。

单向函数的构造过程如下：

1.从一个困难的问题P着手，取出P中的一个子问题P1；

2.对问题P1进行伪装，并使得其得到的问题P2看起来很像原始问题P，用P2作为加密密钥；

3.对如何从P2恢复得到P1的有关信息保密，称该信息为“陷门”；

4.使系统的合法用户能够通过求解容易的问题P1进行解密，而其他用户不得不去求P2。

目前已经出现的公钥密码体制所基于的问题有：

（1）整数分解问题；

（2）Zp上的离散对数问题；

（3）椭圆曲线上的离散对数问题；

（4）线性编码的解码问题；

（5）构造非线性弱可逆有限自动机的弱逆问题。

4 公钥密码的加密解密和数字签名

对公钥密码体制的要求：

用KPi和KCi分别表示第i个用户的公钥和私钥。KPi决定了一个加密Ei，KCi决定了一个解密Di。Ei和Di都可以有效的实现，但{KPi}是一个公开的目录，而KCi第i个用户知道。对所有用户来说，很难从KPi推导出KCi。

如果 Ei和 Di满足：Di(Ei(x))＝x

我们称非对称加密方法满足机密性要求。

如果 Ei和 Di满足：Ei(Di(x))＝x

我们称非对称加密方法满足认证要求。

非对称加密方法：

如果A想发送消息m给B，他从目录中选取标记为B的密钥KPB(这决定了EB)对消息进行加密：A)c＝EB(m)

并在公开信道上将密文c发给B。

B用他的私钥KCB(这决定了DB)来恢复消息m:B)DB(c)＝DB(EB(m))＝m

非对称签名方法：

如果A想发送消息m给B，为了证明这个消息是A发出的，A要用自己的私钥KCA(这决定了DA)对消息进行签名：

A)d＝DA(m)

并在公开信道上将经过签名的密文d发给B。

B从目录中选取标记为A的公钥KPA(这决定了EA)对d进行验证：

B)EA(d)＝EA(DA(m))＝m

因为只有A才会用自己的私钥对消息加密，所以B确信消息是A所发出的。

非对称加密签名方法：

如果A想发送一条加密消息m给B，并加上自己的签名，他首先用自己的私钥KCA(这决定了DA)对消息进行签名：

A1)d＝DA(m)

并将d加到他的签名‘A’中，接下来他从目录中选取标记为B的密钥KPB对(‘A’,d)加密：A2)e＝EB(‘A’,d)

并在公开信道上将e发给B。

B用自己的KCB(这决定了DB)来恢复数对：B1)DB(e)＝DB(EB(‘A’,d))＝(‘A’,d)

B从数对(‘A’,d)中得知A是发送方，然后B用A的公钥KPA从d中恢复m：B2)EA(d)＝EA(DA(m))＝m

B获得了消息m，而且确信消息是A所发出的，因为只有A才会用自己的私钥对消息加密。

5 椭圆曲线在公钥密码系统中的理论基础

椭圆曲线理论是代数、几何、数论等多个数学分支的一个交叉点，它是由Weierstrass方程所确定的三次平面曲线方程，它的一般形式如下：

其中 a、b、c、d、e 是满足一些条件的实数，满足上述方程的数偶(x,y)我们称为椭圆曲线上的点。点O被称为无穷点或零点。那么椭圆曲线可以表示为E＝{(x,y)∈ K×K|y2+axy+by＝x3+cx2+dx+e}∪{O}，E 或者 E/K 就表示有限域K上的椭圆曲线。

对于椭圆曲线，可以定义这样一种形式的加法：如果一个椭圆曲线上的三个点处于一条直线上，那么它们的和为O。从这个定义可以定义椭圆曲线的加法规则：

①O是加法的单位元。O＝－O；对于椭圆曲线上的任意一点 P 有 P＋O＝P。

②一条垂直的线和曲线相交于两个有相同x坐标的点，即P1＝(x,y)和 P2＝(x,-y)。它也和曲线相交与无穷点。因此有 P1＋P2＋O＝O 和 P1＝－P2。 因而一个点的负值是有一个有着相同的x坐标和负的y坐标的点。(如图1)

③要对具有不同的x坐标的两个点Q和R进行相加，先在它们之间画一条直线并求出第三个交点P。容易看出这种交点是唯一的 (除非这条直线在Q和R处是曲线的切线，这时取 P＝Q 或 P＝R)。那么有 Q+R+P＝O,因此有Q+R＝－P。 (如图 1)

④要对一个点Q加倍，画一条切线并求出另一个交点 S。 那么 Q+Q＝2Q＝－S。 (如图 2)

这些加法规则满足正常的加法性质，比如交换律和结合律。一条椭圆曲线上的一个点P被另一个正整数k相乘的乘法被定义为k个P的相加，如3P＝P+P+P。

以上性质说明：椭圆曲线上的点关于运算＋成交换群(Abel群)。椭圆曲线密码体制的算法基础正是建立在这种大数运算的操作上的。

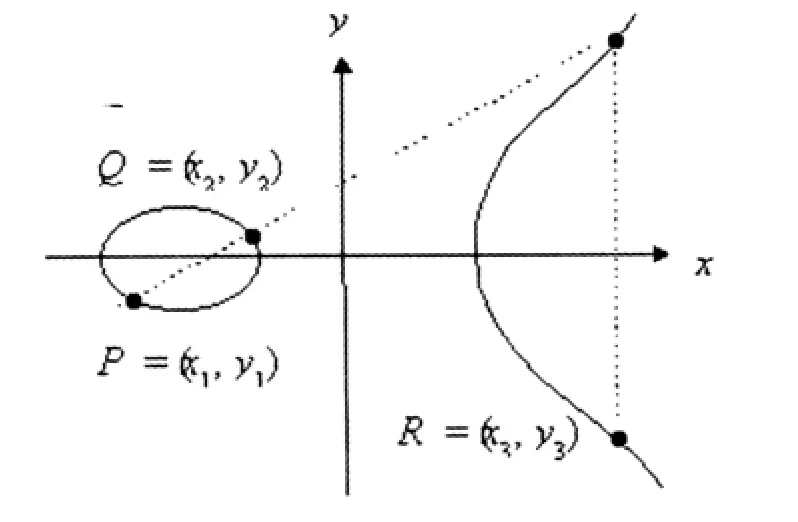
图1 椭圆曲线上的加法P+Q＝R

图2 椭圆曲线上的加法P＋P＝2P＝R

6 基于椭圆曲线密码体制的盲数字签名设计

6.1 数字签名与盲签名

数字签名是公钥密码的一个重要的应用，它在信息安全（包括身份认证，数据的完整性，不可否认性以及匿名性等方面）特别是在大型网络安全通讯中的密钥分配、认证及电子商务系统中，具有重要的作用。简单的说，数字签名就是一种鉴别机制，可以在一个要传送的报文中附带一段起到签名作用的代码。这个签名保证了报文的来源和完整性。

盲签名是需要某人对一个文件签名，但不让他知道文件内容，所以先把消息盲化再让另一个人签名的方法称为为盲签名。

盲签名过程如下图3：

图3 盲签名过程框图

一个盲签名方案是一个包含两个参与者的密码协议：一个用户U和一个签名者S。用户选择一个文件，并从签名者那里得到了签名者对这个文件的签名，却没有对签名者泄露关于这个文件的任何信息，而且即使以后签名者又见到了这个消息签名时，他也无法确定是否是他签署的。

盲数字签名不同于一般的数字签名，它不但具有普通数字签名的全部作用，而且使文件签名过程也变得更加的安全，因为签名者无法泄露关于文件的任何信息，因此，盲数字签名可被用来设计匿名电子现金系统。

6.2 椭圆曲线公钥密码的盲数字签名设计

6．2．1 体制参数

设 T＝(p，a，b，G，n，h) 为椭圆曲线的系统参数，na，Pa分别为签名者A的私钥和公钥；nb，P b分别为用户B的私钥和公钥。

6．2．2 盲签名过程

假设，用户B要求A对B的一个文件进行盲签名：

1)签名者A随机选取一个整数k，(0

计算：Q＝kG，并将Q传送给B；

2)用户B接收到Q后，随机生成一个整数r1，(0

计算：R＝r1Q＝(Rx,Ry)；

3)用户B再随机生成一个整数r2，(0

计算：＝(mr2)mod n 及 r＝(r2Rx)mod n。 并将(，r)传送给A；

4) 签名者 A 计算：＝((na＋r)/k)mod n，完成签名，并将传送给用户B；

5)用户B计算：Y＝(r1-1 r2-1)mod n，输出签名(R,Y)。

签名验证：验证mPa＝YR－RxG，若等式成立，则验证通过，否则签名不正确。

验证公式的证明：

6．2．3 算法的安全性分析

按照盲数字签名方案的特性，明文消息m对于签名者A来说是盲的。所以A在对B进行认证时只能得到加密后的消息，而由得到m相当于解椭圆曲线离散对数问题，所以A不可能看到明文消息m。同样，基于椭圆曲线离散对数问题的难解性，A也不能将盲签名(R，Y)与盲消息对应起来。要伪造签名是不可能的，因为在等式mPa＝YR－RxG中如果先确定Rx，则求解Y相当于求解椭圆曲线离散对数问题，因为要求解Y，必要先求解r1，r2，那么必求解 R＝r1Q＝(Rx,Ry)和 r＝(r2Rx)mod n 这两式，所以求解r1，r2正是求解ECDLP问题；先确定Y再求解Rx是一个指数问题，因为要确定Y，那么需求解Y＝(r1-1 r2-1)mod n，也没有有效解法。因此，本方案满足盲数字签名的要求。

7 结论

盲数字签名以椭圆曲线密码体制的安全性为保证，椭圆曲线密码体制的安全性是基于椭圆曲线离散对数问题的难解性之上的，目前还没有对椭圆曲线离散对数问题的有效解法；合法用户采用椭圆曲线盲数字签名方法处理信息之后，非法用户不能伪造合法用户的签名，因为在不知道合法用户密钥的情况下是不能对椭圆曲线离散对数问题求解的。同样，基于椭圆曲线离散对数的难解性，不可能得知双方交换信息的内容，也无法对截获的信息进行流量分析，重传以及修改或伪造。以此方案，可以满足匿名电子现金系统等方面的安全认证需要。

[1]Mohan Atreya．数字签名[M]．北京：清华大学出版社，2003．

[2]William Stallings．Cryptography and Network Security:Principles and practice Second Edition[M]．北京：电子工业出版社，2001．

[3]DEW AGHE L．Remarks on the schoff－Elkies－Atkin algorithm[M]．Math Comp， 1998,67(223):1247～1252．

[4]MENEZES A,VANSTONE S．Elliptic Public Key Cryptosystems[M]．Bostou Ha－ rdbamd：Kiuwer Acadamic Publishers，l993．

[5]Schoof R．Elliptic curves over finite field and the computation of square roots mod p[M]．Mathematics of Computation．1985,44:483～494．

[6]Robshaw M,Yin Y．Elliptic curve cryptosystems[M]．New York：RSA Labora－ tories，1997．

[7]Menezes A,Okamoto T,Vanstone S．Reducing elliptic curve logarithms to logarithms in afinite field [M]．IEEE TIT，1993,39(5):1639～164．

TP39

A

1674－5787（2010）02－0152－03

2009-12-31

谢扬（1981—），男，重庆市人，工程师，重庆大学通信工程学院硕士研究生，研究方向：通信网络;王金凤(1981—)，女，河北人，重庆电子工程学院软件工程系，讲师，研究方向：网络通信。

责任编辑 王荣辉