一类3-正则图的关联邻点可区别全染色
2010-11-02杨随义王治文
杨随义,王治文
一类3-正则图的关联邻点可区别全染色
杨随义1,王治文2
(1.天水师范学院数学与统计学院,甘肃天水741000; 2.宁夏大学数学计算机学院,宁夏银川750021)
对简单图G(V,E),f是从V(G)∪E(G)到{1,2,…,k}的映射,k是自然数,若f满足(1)∀uv∈E(G),u≠v,f(u)≠f(v);(2)∀uv,uw∈E(G),v≠w,f(uv)≠f(uw);(3)∀uv∈E(G),C(u)≠C(v);其中C(u)={f(u)}∪{f(uv)|uv∈E(G)};则称f是G的一个关联邻点可区别全染色.给出了一类3-正则重圈图Re(n,m)(m≥2,n≥3且n≡0(mod2))的关联邻点可区别全色数.
3-正则重圈图;邻点可区别全染色;关联邻点可区别全色数
图的染色是图论的重要研究内容之一,由计算机科学和信息科学等所产生的一般点可区别边染色[1],邻点可区别边染色(或邻强边染色)[2-5]及D(β)点可区别边染色[6],点可区别边染色[7-8],邻点可区别全染色[9]等都是十分困难的问题,至今文献甚少.在此基础之上,Zhang进一步提出了新的染色概念,图的关联邻点可区别全染色是其中之一[9].本文给出了一类3-正则重圈图Re(n,m)(m≥2,n≥3且n≡0(mod2))的关联邻点可区别全色数.
定义1[9]对于阶数不小于2的连通图G(V,E),f是从V(G)∪E(G)到{1,2,…,k}的映射,k是自然数,如果f满足:
(1)∀uv∈E(G),u≠v,有f(u)≠f(v);
(2)∀uv,uw∈E(G),v≠w,f(uv)≠f(uw);
(3)∀uv∈E(G),C(u)≠C(v);
其中C(u)={f(u)}∪{f(uv)|uv∈E(G)};则称f是图G的关联邻点可区别全染色,也称G有k-关联邻点可区别全染色.(简记作k-I-AVD TC),记为G的关联邻点可区别全色数.
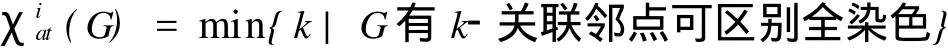
定义2[10]设G(V,E)是简单图,如果m≥2,n≥3且

猜想1[9]对简单图G,则有χiat(G)≤Δ+2,其中Δ是G的最大度.
文中未加说明的术语、记号可参看文献[11,12].
1 主要结论
定理 对于3-正则重圈图Re(n,m)(m≥2,n≥3且n≡0(mod2)),则有
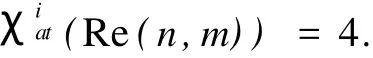
证明 由定义1知,χiat(Re(n,m))≥4,为证明χiat(Re(n,m))=4,仅需给出3-正则重圈图Re(n,m)的一个4-I-AVD TC.如下定义一个从V(Re(n,m))∪E(Re(n,m))到{1,2,3,4}的映射f:
情况1 若m=2,3时,易证χiat(Re(n,m))=4(n≥3且n≡0(mod2))成立.
情况2 当m≥4时,

在下述证明中当j+1>2n时j+1(mod2n).由于各层分布与m的值有关,所以按m进行如下分类:情况2.1当m≡0(mod4)时,


情况2.2 当m≡3(mod4)时,
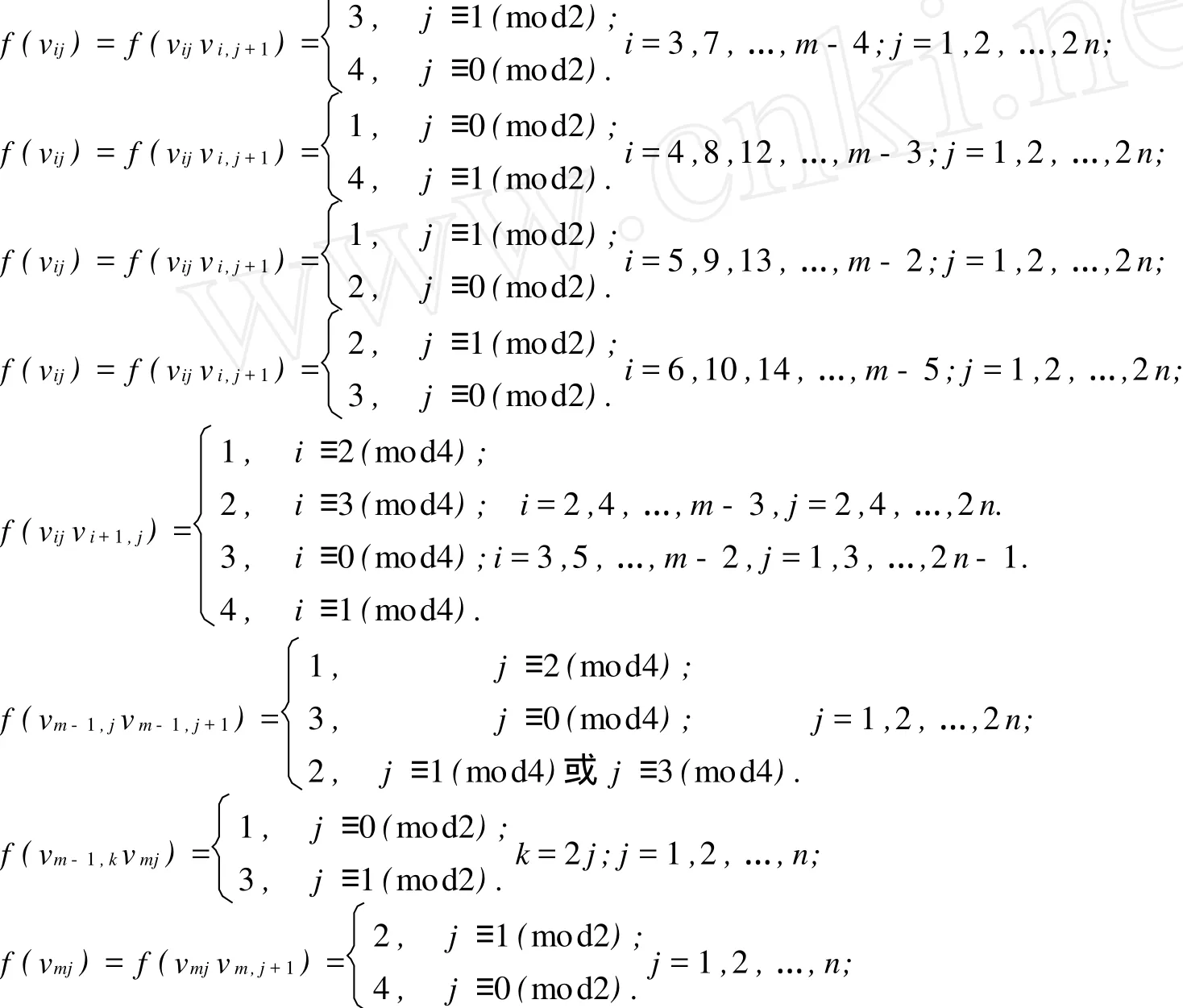
此时


情况2.3 当m≡1(mod4)或m≡2(mod4)时,类似于情况2.1,2.2证明.
综上可知,f是3-正则重圈图Re(n,m)(m≥2,n≥3且n≡0(mod2))的一个4-I-AVD TC.
[1] BURRIS A C,SCHELP R H.Vertex-distinguishing Proper Edge-coloring[J].J Graph Theory,1997,26(2):73-82.
[2] BALISTER P N,GYORI E,L EHEL J,et al.Adjacent Vertex Distinguishing Edge-colorings[J].S IA MJ Discrete Math, 2007,21:237-250.
[3] HATAMI H.Δ+300 is a Bound on the Adjacent Vertex Distinguishing Edge Chromatic Number[J].J ournal of Combinatorial Theory,SeriesB,2005,95:246-256.
[4] ZHANG Z,LIU L,WANGJ.Adjacent Strong Edge Coloring of Graphs[J].A ppl Math Lett,2002,15:623-626.
[5] ZHANG Zhong-fu,LI J,CHEN X,et al.D(β)-vertex-distinguishing Proper Edge-coloring of Graphs[J].Acta Math Sinica(Chin Ser),2006,15:703-708.
[6] ZHANG Z,QIU P,XU B,et al.Vertex-distinguishing Total Coloring of Graphs[J].A rs Comb,2008,87:33-45.
[7] 张忠辅,李敬文,陈祥恩.图的距离不大于β的点可区别的全染色[J].中国科学,2006,49(10):1430-1440.
[8] ZHANG Z,CHEN X,LI J,et al.On Adjacent-vertex-distinguishing Total Coloring of Graphs[J].Sci Chins(S ER A), 2005,48(3):289-299.
[9] CHANG C(ZHANG Z),WOODALL D R.LIJ,et al.Incidence Adjacent Vertex-distinguishing Total Coloring of Graphs
[R].兰州交通大学科学报告,2008,2:1-8.
[10] ZHANG Z.The Smarandachely Adjacent Vertex Total Coloring of Graphs[R].兰州交通大学科学报告,2009,2-3.
[11] BONDYJ A,MURTY U S R.Graph Theory with Applications[M].London:Macmillan;New York:Elsever,1986.
[12] 王治文,徐保根,闫丽宏,等.关于圈的广义Mycielski图的全染色[J].山西大学学报(自然科学版),2008,31(4):20-23.
Incidence Adjacent Vertex-distinguishing Total Coloring of a Kind of 3-regular Graph
YANG Sui-yi1,WANG Zhi-wen2
(1.College of Mathematics,Tianshui Normal University,Tianshui741000,China; 2.School of Mathematics and Computer Science,Ningxia University,Yinchuan750021,China)
LetGbe a simple graph andkbe a positive integer.Iffis a mapping fromV(G)∪E(G)to{1,2,…,k},such that(1)∀uv∈E(G),u≠v,f(u)≠f(v);(2)∀uv,vw∈E(G),u≠w,f(uv)≠f(vw);(3)∀uv∈E(G),C(u)≠C(v),we say thatfis a incidence adjacent vertex-distinguishing total coloring ofG,where C(u)={f(u)}∪{f(uv)|uv∈E(G)}.The minimal number ofkis called as the incidence adjacent vertexdistinguishing total chromatic number ofG.The incidence adjacent vertex-distinguishing total chromatic number of 3-repeated cycle graph is disussed.
3-repeated cycle graph;incidence adjacent vertex-distinguishing total coloring;incidence adjacent vertex-distinguishing total chromatic number
O157.5
A
0253-2395(2010)03-0354-04
2009-11-01
国家自然科学基金(10771091);宁夏大学科学研究基金((E)ndzr09-15)
杨随义(1977-),男,讲师,主要从事代数图论的研究.通讯作者王治文,E-mail:w.zhiwen@163.com
