无重复因析试验中一种散度效应的估计方法
2010-11-02李济洪
王 钰,李济洪
无重复因析试验中一种散度效应的估计方法
王 钰,李济洪*
(山西大学计算中心,山西太原030006)
在无重复因析试验的多个散度效应分析中,现有的许多方法都存在错误识别的现象,即两个显著的散度效应可能在它们的交互列上产生一个错误的(spurious)散度效应.为了解决这种模棱两可性,文章提出了一种基于闭的位置效应集合残差的改进H方法(称为AH方法),证明了AH的估计的无偏性,并通过一个基于实例的模拟验证了此方法.
多个散度效应;无重复因析;无偏性;模拟
0 引言
无重复因析试验中散度效应的分析近年来得到了许多学者的关注.最早Harvey[1]从一般回归模型的角度考虑了散度参数的估计问题,提出了一个H估计方法.而Box和Meyer[2]于1986年最先从试验设计的角度提出了一个无重复因析试验中散度效应的分析方法.接着Wang[3],Bergman和Hynén[4],Brenneman和Nair[5]分别研究了此问题,提出了基于对数散度模型的不同散度效应识别和估计方法.最近,McGrath和Yeh[6],Chen-Tuo Liao[7],van de Ven[8]又分别从各种角度出发,给出了一些新的散度效应估计方法和研究结果.但是在多个散度效应的分析中,上面提到的方法都存在错误识别的现象,即两个显著的散度效应可能在它们的交互列上产生一个错误的散度效应.为了解决这种模棱两可性,McGrath and Lin[9]曾提出了一个基于闭的位置效应集合残差样本方差的检验统计量.本文就是在此基础上,把上述闭的位置模型应用于H估计,给出了一种新的估计方法,记为AH估计.接着讨论了AH估计的无偏性,并通过一个基于实例的模拟验证了此方法.
考虑位置散度模型

模型(1)称为位置效应模型,是利用响应的均值对因子效应建模;模型(2)称为散度效应模型,是利用响应的方差对因子效应建模.在试验设计中就是要首先识别出对位置和散度有显著影响的因子效应,然后设置因子的水平使得响应的方差达到最小,均值尽可能接近目标值.而在显著效应的识别过程中,又需要首先给出因子效应的估计,然后借助于半正态概率图,Lenth方法等识别显著的因子效应.因此可见,因子效应的估计尤为重要.
在模型中,y=(y1,y2,…,yn)′是观测值向量,x′i是n×p维设计矩阵X的第i行;X=(X1,X2,…,Xp),p
假定:
1.S(k+)={j:Xk,j=+1}记因子k的正水平的行标的集合;S(k-)={Xk,j=-1}记因子k的负水平的行标的集合,其中Xk,j是Xk的第j个元素.
2.记k1=k2°k3,如果Xk1可以通过Xk2和Xk3的对应元素相乘得到,例如因子A和B的交互项AB=A°B.
3.如果集合S对于运算°是封闭的,则称它为闭集,记为S.
4.L={I,l1,…,lp-1}和D={I,d1,…,dq-1}分别记显著的位置和散度效应集.
1 A H估计方法及其性质
在无重复因析试验中,无论是位置还是散度效应的研究,效应稀疏原则常常被假定,即只有大约30%的效应被认为是显著的.所谓的效应鉴别就是识别出显著的位置和散度效应.而位置效应的鉴别问题已经被广泛的研究,相关文献可参考Hamade和Balakrishnan[10]的综述文章.在本文中总假定正确的位置模型已经被识别,主要考虑散度效应的估计问题.
^β对于对数线性散度模型,如果记{ri,i=1,2,…,n}为拟合位置模型以后得到的残差,即ri=yi-x′i^β,^β为β的普通最小二乘估计,那么对散度效应因子k,Harvey[1]提出H方法可以表示为:
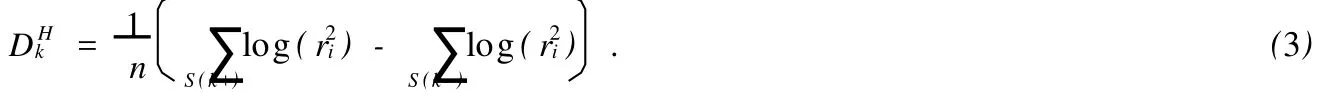
McGrath和Lin[9]曾提出了一个基于闭的位置效应集残差样本方差的ML检验统计量,此闭的位置效应集包括四部分: 1.总均值项;2.显著的位置效应以及它们的交互效应列;3.显著的散度效应以及它们的交互效应列;4.上面所有列的交互列.例如:如果L={I,A,B},D={I,C,D},那么拟合的闭的位置效应模型~L={I,A,B,AB,C,D,CD,A C,A D,A CD,BC,BD, BCD,ABC,ABD,ABCD}.本文就是把拟合此位置模型的残差应用于H方法,然后得到了一种新的散度效应估计方法,称为AH估计.如果记{~ri,i=1,2,…,n}为拟合的残差,则散度参数φk的AH估计可以表示为如下形式:

接下来考虑AH估计的无偏性,为证明的方便首先给出几个引理.
引理1[5]记L={I,l1,…,lp-1},k∈{2,…,n},Lk={k,k°l1,…,k°lp-1},则拟合位置模型LEK=L∪Lk得到的残差有如下形式:

引理2[5]在给定模型(1)下,φk的AH估计的期望
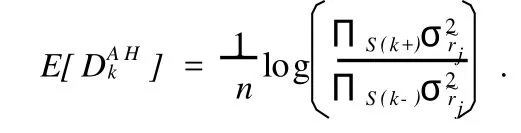
定理 如果¯L记闭的位置效应集,¯D记显著散度效应的闭集,并且dim¯L≤n/2,则对任意的k∈¯D⊆~L,DAHk是无偏的.
证明 由¯L构造,我们知道它肯定是一个闭集,并且可以写为引理1中LEk的形式,那么由引理1和引理2
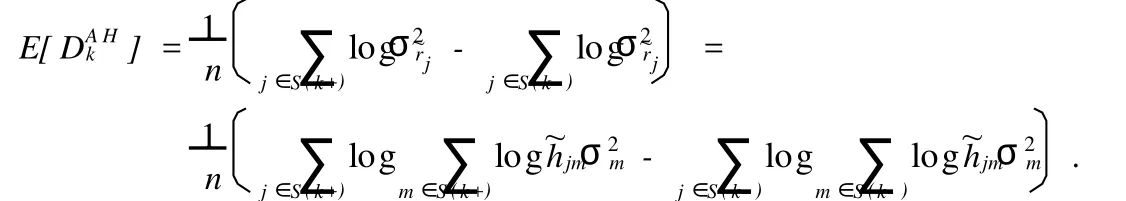
记{Si,i=1,…,M}为¯L所对应的设计矩阵的M个不同的行的组合,则由¯L的闭集性质,有∀j,m∈Si,x′jxm=p;j∈Si,m∈Si′,i≠i′,x′jxm=0.并且对j,m∈Si,当j=m时,~hjm=1-p/n,当j≠m时,~hjm=-p/n.(详细的证明见文献[11])不妨设S(k +)={S1,…,SM/2},S(k-)={SM/2+1,…,SM},又因为k∈¯D⊆¯L,类似地记φ¯L={φ0,φl1,…,φlq},q=dim¯L,那么AH估计的期望

又对任意的j,m∈Si,x′j=x′m,

对任意j∈Si,m∈Si′,i≠i′,

这样,(4)可以写为证明完毕.

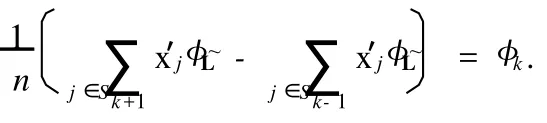
2 一个基于实例的模拟分析
本节考虑一个最早的由Davies[12]提出,后被Bergman和Hynén[4],McGrath和Lin[9]都分析过的染料质量的实例,它使用了一个25-1V部分因析设计,五个试验因子分别是温度(A),原始材料(B),减压(C),烘炉干燥压力(D),真空漏泄(E).表1中给出了它的设计矩阵和响应,所有的作者都发现因子D对位置有较大的影响,关于显著的散度效应,McGrath和Lin[9]鉴别出了因子E,而Bergman和Hynén[4](BH方法)发现除了因子E之外还有D,D E.但是我们知道BH方法存在错误识别的现象,下面我们就通过基于此实例的模拟来给出本文方法和BH方法,H方法的一个对照.
具体地,假定真正的位置模型是L={I,D},散度模型是D={I,D,E},βD=33,φD=φE=2,模拟次数为5 000次.模拟结果见表2.

表1 设计矩阵和响应Table 1 Design Matrix and Responses

表2 基于实例的模拟对照Table 2 Simulateed Comparison Based on Real Example
从表2中我们可以看到BH方法高估了因子D E,偏度达到了1.56,从而在识别中肯定会错误识别D E,而H方法虽然无偏的估计出了D E,但它却低估了因子E,从而可能会丢掉显著的因子E.对于AH方法,它无偏的估计出了因子D,E,D E,并且AH估计的均方误差一致地比BH方法和H方法小,比如AH方法使因子D E的均方误差从BH估计的2.78,H估计的0.43减小到了0.36.从而可见本文方法可以用于多个散度效应的参数估计问题研究,不会出现对参数的高估和低估现象,保证散度效应的正确识别.
3 讨论
在试验设计中,效应稀疏原则是最基本的三大原则之一,即在所有因子效应中至多有30%的效应是显著的,那么在此原则下对于一大类位置散度模型,定理条件dim¯L≤n/2常常可以满足,并且本文中提到的所有方法都是在效应稀疏原则下得到的.当dim¯L≤n/2不能满足时,无法给出一个精确的条件来保证散度参数估计的无偏性.特别地,当dim¯L=n/2时,对于任意的k∉¯L,因子k都是不可估的,相关的参考文献见Brenneman和Nair[5].
当模型假设不正确时,本文方法同样适用,可以直接推广.但方法的性质需要作进一步的探讨,比如此时可能得不到参数估计的无偏性,只能给出一个近似无偏的条件,这也是我们下一步要做的工作.
[1] HAVREY A C.Estimating Regression Models with Multiplicative Heteroscedasticity[J].Econometrica,1976,44:461-465.
[2] BOX G E P,MEYER R D.Dispersion Effects from Fractional Designs[J].Technometics,1986,28:19-27.
[3] WANG P C.Tests for Dispersion Effects from Orthogonal Arrays[J].Computational Statistics and Data A nalysis,1989, 8:109-117.
[4] BERGMAN B,HYNÉN A.Dispersion Effects form Unreplicated Designs in the 2k-pSerises[J].Technometrics,1997,39: 191-198.
[5] BRENNEMAN W A,NAIR V N.Methods for Identifying Dispersion Effects in Unreplicated Factorial Experiments:A Critical Analysis and Proposed Stra tegies[J].Technometrics,2001,43:388-404.
[6] MCGRATH R N,YEH A B.A Quick,Compact Two-Sample Dispersion Test:Count Five[J].The A merican Statistician, 2005,59:47-53.
[7] LIAO Chen-Tuo.Two-level Factorial Designs for Searching Dispersion Factors and Estimating Location Main Effects[J]. J ournal of Statistical Planning and Inf erence,2006,136:4071-4087.
[8] VAN de VEN P M.On the Equivalence of Three Estimators for Dispersion Effects in Unreplicated Two-level Factorial Designs[J].J ournal of Statistical Planning and Inf erence,2008,138:18-29.
[9] MCGRATH R N,LIN KJ.Testing Multiple Dispersion Effects in Unreplicated Fractional Factorial Designs[J].Technometrics,2001,43:406-414.
[10] HAMADA M,BALAKRISHNAN N.Analyzing Unreplicated Factorial Experiments:A Review with Some New Proposals[J].Statistica Sinica,1998,8:1-41.
[11] BRENNEMAN W A.Inference for Location and Dispersion Effects in Unreplicated Factorial Experiments[J].Unpublished Ph D dissertation.University of Michigan,Statistics Department.
[12] DAVIES O L.Design and Analysis of Industrial Experiments[M].London:Oliver and Boyd,1956.
A Estimator of Dispersion Effects in Unreplicated Factorial Experiments
WANG Yu,LI Ji-hong
(Computer Center,Shanxi University,Taiyuan030006,China)
In the analysis of multiple dispersion effects for unreplicated factorial experiments,there often exists the phenomenon for picking up factors spuriously,that is,two active dispersion effects may create a spurious dispersion effect in their interaction column,and the most existing methods are subject to these spurious effects.To resolve the ambiguousness,a adapted H method(called the AH method)was introduced based on residuals from the fitted closed set of location effects.The unbiased condition of the AH estimator was proved,and the simulations based on a real example were used to illustrate the results.
multiple dispersion effects;unreplicated factorial;unbiasedness;simulation
O212.1
A
2009-01-15;
2009-02-05
国家自然科学基金(60873128)
王 钰(1981-),男,助教,硕士,主要从事概率统计研究.E-mail:wangyu@sxu.edu.cn,*通讯联系人E-mail: lijh@sxu.edu.cn
0253-2395(2010)02-0186-04
