图类αKa∪βCP(b)中的整谱图
2010-11-02景占策侯耀平
景占策, 侯耀平
(1.青海师范大学数学系,青海西宁 810008; 2.湖南师范大学数学与计算机科学院,湖南长沙 410081)
图类αKa∪βCP(b)中的整谱图
景占策1, 侯耀平2
(1.青海师范大学数学系,青海西宁 810008; 2.湖南师范大学数学与计算机科学院,湖南长沙 410081)
设图G是一个简单图,图G的补图记为¯G,如果G的谱都是整数,就称G是整谱图.鸡尾酒会图CP(n)=K2n-n K2(K2n是2n阶完全图)和完全图Ka都是整谱图[1].本文确定了图类中的所有整谱图.
整谱图;主特征值;丢番图方程;鸡尾酒会图;完全图
1 引 言
设G是一个简单连通图,G的邻接矩阵A(G)的特征值和特征向量称为图G的特征值和特征向量. G的一个特征值μ称为主特征值,如果G有一个相应于μ的各分量之和不为零的特征向量.由非负矩阵的理论知,图的最大特征值(谱根)总是它的主特征值.一个图恰有一个主特征值当且仅当它是正则图.对恰有k(k≥2)个主特征值的图的刻划是图谱理论中的一个长期待解决的公开问题.如果G的谱完全由整数组成,我们就说G是整谱图.Mirko Lepovic对恰有两个主特征值的整谱图的补图做了较多研究,得到了一些很好的结果[4-8].

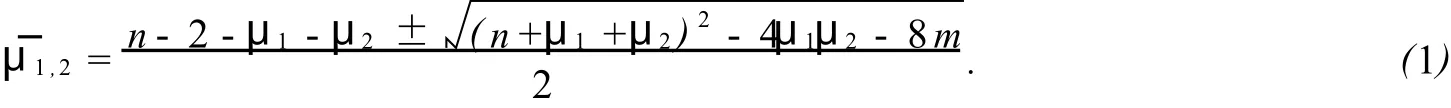

2 主要结论的证明及应用
现在我们刻画类整谱图(α,β,a,b∈N,a-2b+1≠0).




[1] 柳柏濂.组合矩阵论[M].北京:科学出版社,2005:10-50.
[2] 侯耀平.恰有两个主特征值的树[J].湖南师范大学自然科学学报,2005,28(2):1-3.
[3] Lepovic M.Some results on graphs w ith exactly two main eigenvalues[J].Univ.Beogra Publ.Elektro-tehn. (Ser.Mat),2001,12(2):68-84.
[4] Lepovic M.On integral graphs w hich belong to the class[J].J.App l.Math.&Computing,2004, 14(1-2):39-49.
[5] Lepovic M.On integral graphs w hich belong to the class[J].Graphs and Combinatorics,2003,19:527-532.
[6] Lepovic M.On integral graphs w hich belong to the class[J].Discrete Mathematics,2004,285:183-190.
[7] Lepovic M.On integral graphs w hich belong to the class[J].Univ.Beograd.Publ.Fak.Ser. Mat.,2006,17:52-59.
[8] Lepovic M.On integral graphs w hich belong to the class[J].J.App l.Math.&Computing,2006, 20(1-2):61-74.
On In tegral Graphs Which Belong to the ClassαKa∪βCP(b)
J ING Zhan-ce1,HOU Yao-ping2
(1.Department of Mathematics,Qinghai No rmal University,Xining,Qinghai 810008,China; 2.College of Mathematics and Computer Sciences,Hunan No rmal University,Changsha,Hunan 410081,China)
LetGbe a simp le graph and let¯Gdenote its complement.A graphGis called integral if its spectrum consists entirely of integers.Cocktail party graphsCP(n)=K2n-n K2and complete graphsKaall are integral graphs[1]. This paper determines all the integral graphs of
integral graphs;main eigenvalues;Diophantion equation;Cocktail party graphs;comp lete graphs
O157.5
A
1672-1454(2010)02-0113-05
2007-07-14
湖南省教育厅科学研究资助项目(06A 037)
