滑坡蠕变时效稳定性理论与滑坡预测(报)研究的基本构想
2010-11-02杨人光
杨人光
(中国四海控股有限公司生态灾害测控中心,北京 100081)
滑坡蠕变时效稳定性理论与滑坡预测(报)研究的基本构想
杨人光
(中国四海控股有限公司生态灾害测控中心,北京 100081)
滑坡的形成过程显示出其时效特征,已有研究显示滑坡的时效特征有助于滑坡的精确预测预报研究。本文在马克斯韦尔、开尔文、斋滕迪孝等人的研究基础上引入了岩土体粘-弹性滞后系数,以岩土材料试件在各种受力状态下的实际监测轨迹曲线为依据,采用拟合法,遵循曲线拐点形变量和形变率连续性导出关于时间的二元非线性超越代数方程组,并求得时效共轭点时间和剧滑失稳时间,最后得到滑坡蠕变时效可预测性的结论。
滑坡;蠕变;粘-弹性滞后系数;时效共轭点;时效稳定性
1 前言
滑坡是斜坡岩土体沿着贯通的剪切破坏面所发生的滑移现象,是地表的地质灾害之一。国内外众多学者与工程技术人员进行了大量室内外监测试验和探索性研究,积累大量资料,并在滑坡稳定性与监测预报的研究中形成了许多科学的概念和思路。
近半个世纪以来,就滑坡体稳定性研究,多数的国内外学者及工程技术人员遵循经典力学思维框架,从滑坡体受力角度或地质力学角度,应用岩土力学中的有限元、离散元等数值分析法,试图揭示出非均质各向异性,非规则分布结构面的岩土体的应力应变状态,并以微元体主应力分布积分及强度指标,再结合极限平衡方法确定滑坡滑动优势面,导出滑坡稳定性系数Ksf。它无疑是滑坡稳定性判据的重要依据,但缺乏时间的内涵,作为滑坡的判据准则,就有商榷的余地,正如崔政权教授(系统工程地质导论著者)所述在确定论分析中,指标Ksf≥1,表示边坡处于稳定,或者说是安全的,问题是这一安全究竟有多大把握性的问题。为此,又引用以概率论为基础的置信度或可靠性分析等,这种以纯静态力学分析法去研究滑体蠕变运动,类同“静不定”问题当作静定处理岂能奏效?
滑坡的形成有其特有的过程,该过程极其复杂且受多方面的因素影响,如:局部地质结构破坏、地应力释放、水的浸泡和蚀化作用、周边环境(坡脚冲刷、重复性微震动等)以及气候状况影响等诸多因素。根据滑坡类型,探求滑坡的稳定性系数,在求解过程中的分析方法,便涉及到诸多的物理力学性质参数,参数的正确选取必然要利用多种手段和方法,但“未能取得令人满意的效果”。
总之,滑坡的稳定性问题,是岩土体结构及模型材料的基础性理论课题,并非仅依赖于传统经典力学构架范畴。至于是否系与现代边缘性学科的交叉呢?也不得而知。作者以为任何基础性学科应遵循着学科固有的抽象模型和运动规律,这就驱使作者去追逐新思路,重新确立新的理念。
2 研究现状
可喜的是,国内外有许多学者走出经典力学的思维框架,从滑坡监测预测入手,建立岩土体流变(包括蠕变)的物理数学模型,如马克斯韦尔(C. Maxwell)体或沃伊特(Voigt)和开尔文(Kelvin)体。尤其是马克斯韦尔粘-弹性滞后物理模型和开尔文的数学模式,两者相结合即为粘-弹性滞后模型。在恒定载荷力作用下,作者把它改写为二阶微分方程式,即:引进了岩土体粘-弹性滞后系数E、η分别为岩土弹性模量和粘滞性系数。它尽可拟合岩土稳定蠕变时段,然而,却不能推广于蠕变全过程,因为靠单一渐变线性方程是无法预测(报)失稳突变时间的。故它被搁浅了,因而诸多科技人员从临滑实测蠕变轨迹曲线,采用回归多项式方程,梯度-正弦或者应用流变方程等拟合外推,即拟合法,有人也简称为“灰色理论”的组成部分,实际上往往把滑坡体初始萌发的流变时段加以拟合外推,就带有经验性和揣测性,同样是不能奏效。
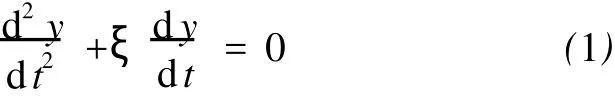
但近半个世纪来,诸多学者作出了大量在拉、压、弯曲、扭转的受力状态下,施加不同载荷比的岩土试件的滞后形变轨迹曲线。并且指出“滑坡剧滑时间就是在该曲线上寻求时间增量Δt→0位移增量Δs→∞的那一点”,这犹如在灰暗荒原燃起一垛智慧的篝火。
特别是1965年日本斋滕迪孝等人在室内沙土盘蠕变时效试验基础上提出第(Ⅲ)阶段(作者称之为失稳蠕变)数学模式,即

式中,A、α为待定系数。
在此基础上提出第(Ⅲ)蠕变阶段滑坡时间预报的经验公式,因限于试验条件,他们忽略了初期的稳定时段或者寓于线性稳定蠕变时段如图1。导致其误差幅值就相差十几倍(即10±0.59)。可惜人们连同斋滕迪孝先生提出失稳时段的数学模式也缺乏应有的关注。

图1 土质斜坡等速蠕变速率与达到破坏时间关系图解Fig.1 Illustrate the relation between the constant rate creep and the time to failure of soil slope
这就是当前岩土蠕变学理论,滑坡稳定性以及预测预报理论模式研究、探索的基本成果和认同状况。
3 岩土体蠕变时效稳定性理论与滑坡预测预报研究的基本构想
作者以为马克斯韦尔、开尔文、斋滕迪孝等人所探索出上述基本成果是卓越的,是开拓性的,是铸造出一块块堆放着的构筑蠕变学或者说岩土结构稳定性理论大厦的基石。
3.1 已有研究成果的启示
(1)斋滕迪孝先生以沙土盘室内蠕变时效试验为依据归纳出二阶微分方程式,作者从中受到极大的启迪。因为该微分方程数学模式是非线性的,量化了滑坡体从渐变到突变的演化,并且不含有受力状态的显式项。故而该数学模式有望适合于岩土体在各种复合受力状态下失稳蠕变时效性,赋予它普遍性的特征。作者根据该方程的解,拟合蠕变后期实际监测赋值点,便预测(报)出滑坡体短期或临滑的剧滑时间tf,因而它不失为失稳时段的可预测预报性。
(2)马克斯韦尔、开尔文的粘-弹性滞后体的数学模式,恒定载荷力对时间的导数后亦不含有载荷项,作者把它改写为二阶微分方程式。如式(1)所示,它描述前期稳态时段形变时效的规律,引出一个尚待共认的岩体材料的粘-弹性滞后体的物性参量,以它来度量岩土材料的时效性的强弱,它是岩土脆性材料所特有的,即呈现出粘-弹性滞后特性。为拟合实际监测曲线求解,反馈出岩土材料参量ξ,这就是规律的可认识性与和谐性。因为对岩土体而言,严格来说,参量ξ完全相同的岩土块体是不存在的,更何况参与滑坡体蠕变时效并非滑块自身而是滑动面的岩土介质。
(3)参量ξ制约着蠕变全过程,所谓可预测性是指稳定时段终端,即失稳点,与它贴近的失稳伊始时段就预测出滑体剧滑时间tf,因而稳定时段是可预测预报性不可或缺的组成部分。
3.2 基本研究构想
作者的工作就是将那一块块堆放着的基石构筑起一座大厦。首先要论证以下两道关键性的问题。
(1)原本孤立量化出的岩土材料蠕变时效形变两个二阶微分方程(1)、(2)式,作者把它分别确认为稳定和失稳蠕变时段的数学模式,它们能否拟合在同一条蠕变时效监测轨迹曲线上呢?其联立求解能否相互耦合,是否存在一个唯一的共轭点呢?即在曲线连续条件下求解出轨迹曲线的拐点,即时效共轭点时间tp。
(2)滑体一旦进入稳定转向失稳伊始时段赋值点(即紧贴着拐点)能否就预测预报出其剧滑时间tf,即赋予微分方程组的可预测预报性呢?
为此,作者以岩土材料试件在各种受力状态下的实际监测轨迹曲线为依据,采用(1)、(2)式微分方程解的拟合法,遵循曲线拐点形变量和形变率连续性导出关于以tp、tf为未知量的二元非线性超越代数方程组,论证其函数方程在tp、tf的时域范围内函数值发生变化,则函数有零解。并应用多重二分法数值程序求解得出实数根tp、tf,最终才成功地锁定(1)、(2)式微分方程联立确认为岩土蠕变时效微分方程组,即岩土材料蠕变学理论的基本方程,以揭示出岩土材料在恒定施加载荷作用下,随时间推移而发生形变的时间效应,暂称为蠕变时效规律。作者抓住马克斯韦尔、开尔文粘-弹性时效性模式和斋滕迪孝非线性微分方程,才导出岩土蠕变的可预测性。
同时应指出,在以上两道关键性问题论证时,蠕变时效载体的规律是指岩土整体所呈现出宏观规律。如同岩土材料试件是指试件整体的形变量或者整体位移量的宏观规律。这是岩土体自身物理力学性质参数,以及各点位微元体形变的无规律性,却呈现出整体宏观的规律性。
至此,读者将会提出一个深层次的问题:(1)、(2)式二阶微分方程均不含有载荷项,如何反映出施加于试件上的载荷比β,或者它的倒数即滑坡稳定性系数Ksf在岩土材料蠕变时效规律中内在关系,或者说能否赋予Ksf更深刻的内涵。
为此作者在论证(1)、(2)方程组彼此耦合、并求解蠕变时效共轭点唯一性的同时,就演绎出方程组各参量数和施加载荷比β独立的相关函数关系的曲线族。并且发现时效稳定指数α曲线族却重合出一条曲线。α-β相关函数曲线与岩土试件材料物性ξ以及受力状态(拉、压、弯曲、剪切、扭转)无关,作者称之谓α-β规律关系曲线。其实α为方程(2)式的无因次指数,故之α-β规律关系与方程(2)式是相和谐的。因而从任何滑坡监测出轨迹曲线,演释出α值,则可由α-β规律关系曲线图反查出β值。它的倒数即为滑坡稳定性系数Ksf。因此蠕变时效方程组才赋予Ksf的稳定时间(年限)的内涵。对于滑坡体而言,严格来说,唯有滑体监测出轨迹曲线方可给出有可信度的Ksf。
滑坡稳定性系数Ksf定义和清晰概念的确立,不难确认所谓滑坡理论即为滑坡稳定性理论。那么如何更确切赋予蠕变时效方程组(1)、(2)式以及时效共轭点物理力学性的含义呢?
作者应用量纲分析法,从(1)、(2)二阶微分方程式出发,导出蠕变时效系统的无因次数,其中唯时效共轭点(tp、yp)组合参数

当ve=1,岩土结构处于永久稳定;
当ve>1,岩土结构从稳定转向失稳蠕变。
故ve具有判断岩土结构从稳定转向失稳的特征,故称ve为结构失稳判据,则其共轭点即为失稳点。于是岩土材料粘-弹性时效模型、稳定时段方程式(1)和失稳非线性时效方程式(2),它们构成岩土蠕变时效稳定性理论的基本方程组。滑坡稳定性系为岩土结构稳定性一个最典型的特例。其实,凡在恒定重力场驱动下地壳板块、区域性地块以及地表上下的建筑物和构筑物等均涉及蠕变时效稳定性问题,并揭示出蠕变时效稳定性一般性原理。
通过分别论述蠕变时效可预测性、低值载荷比β相关函数分析,导出失稳时段“自拟合”规律与岩土抗形变极限强度时效性,蠕变时效方程组的积分导出蠕变能量累积、贮存和瞬息释放机制。并应用现代数值程序模拟试验分析法,探求区域性地块超巨大能量参量数的内在关系。
[1]胡海涛,项式均.关中西部滑坡的结构、构造特性及稳定性分析[J].地质学报,1965,45(3).
[2]李四光.地质力学[M].科学出版社,1976.
[3]谷德振.岩体工程地质力学基础[M].科学出版社,1976.
[4]西德G,哥德赫(编),张清,张弥(译).有限元法在岩土力学中的应用[M].中国铁道出版社,1983.
[5]杨人光.爆破抛体加速运动的渗流模型[J].力学学报,1984,16 (1).
[6]张倬元.工程地质分析原理[M].地质出版社,1985.
[7]C C维来洛夫.土力学的流变原理[M].科学出版社,1988.
[8]王思敬,1987全国滑坡学术讨论会滑坡论文集[C].四川科学技术出版社,1989.
[9]国际滑坡与岩土工程学术会议论文集[C].华中理工大学出版社,1991.
[10]崔政权.系统工程地质导论[M].水利电力出版社,1992.
[11]张倬元.国际滑坡研究进展——第六届国际滑坡学术讨论会述评[J].中国地质灾害与防治学报,1993,4(3).
[12]晏同珍,等.滑坡文集第十集[C].中国铁道出版社,1993.
[13]杨人光,孙善平.人工爆破治理火山灾害可行性探讨[M].地震出版社,1994.
[14]文宝萍,李缓.黄土地区典型滑坡预测预报及减灾对策研究[M].地质出版社,1997.
[15]郑颖人.边坡与滑坡工程治理[M].人民交通出版社,2007.
[16]殷跃平.汶川地震与滑坡灾害概论[M].地质出版社,2009.
AGING STABIL ITY THEORY OF LANDSL IDE CREEP AND BASIC CONCEPTIONOF LANDSL IDE PRED ICTION
YANG Ren-guang
(CHina Sihai Holdings Co.,L td,Beijing100081,China)
Formation of landslide show s its aging characteristics w hile it is revealed by the existing researches that the aging characteristics of landslide can help to p redict and fo recast the landslide p recisely.On the basis of research findings achieved by Maxwell,Kelvin and Saitou Susumu Takashi etc.,the viscoelastic lag coefficient of rock-soilmass is introduced in this paper, together w ith the p ractical monito ring geometric locus of test piece of rock and soil materials under different strained conditions,and then the fitting p rocess is adop ted.On the p remiseof follow ing the continuitiesof both defo rmation and degreeof defo rmation of knee of curve,the binary nonlinear transcendental algebraic equations concerning time is deduced,and also the time of aging conjugate point and destabilization time caused by severe sliding are calculated,finally the conclusion in w hich the ageing of landslide creep can be p redicted is obtained.
landslide;creep;viscoelastic lag coefficient;aging conjugate point;aging stability
P642.22
:A
1006-4362(2010)02-0071-03
杨人光(1939- ),男,原中科院力学所研究员,现任中国四海控股有限公司生态灾害测控中心总工程师,长期致力于岩土理论与实践,主编的《控制爆炸技术研究与应用》获国家一等奖。
2010-03-26改回日期:2010-04-29
