非线性Hoek-B row n强度折减技术

符文熹,王启鸿,刘长武

(1.四川大学水力学及山区河流保护国家重点实验室,水利水电学院,成都 610065; 2.中国水电顾问集团西北勘测设计研究院工程分院,兰州 730050)

非线性Hoek-B row n强度折减技术

符文熹1,王启鸿2,刘长武1

(1.四川大学水力学及山区河流保护国家重点实验室,水利水电学院,成都 610065; 2.中国水电顾问集团西北勘测设计研究院工程分院,兰州 730050)

为精确执行非线性Hoek-Brow n(HB)强度折减,首先在p-q空间分析了HB曲线任意点切线与Mohr-Coulomb(MC)准则的对应关系,推求了HB屈服函数材料折减系数和强度折减系数的关系,提出了潜入强度折减系数的HB弹塑性分析模型,介绍了在Flac3D平台上二次开发实现非线性HB强度折减的基本思路。对一边坡算例用本文方法和简化Bishop法进行了对比分析,计算结果表明,潜入强度折减系数的HB弹塑性模型计算获得的边坡潜在滑动面形态、位置和相应的安全系数,与简化Bishop法计算结果很接近。

Hoek-Brow n准则;Mohr-Coulomb准则;强度折减;安全系数

1 前言

现有的强度折减理论[1～8]多针对线性Mohr-Coulomb(MC)准则,有关非线性强度折减技术的报道却较少。当前学术界普遍认为Hoek-Brow n (HB)准则能较好地描述节理岩体非线性破坏特征。对于2002版HB准则[9],进行强度折减时大多基于Hoek推求的等效MC强度参数[9],直接用MC强度折减方法。作者所知的只有为数不多的有关非线性HB强度折减方面的报道[10～12]。文献[10]利用HB曲线任意点切线对应的MC强度参数进行折减,采用了现有的MC强度折减方法。文献[11]针对HB准则(1980版),用单轴抗压和抗拉两个破坏应力状态,推求出MC强度折减系数与HB材料参数折减系数之间的关系,但是要对2002版通用HB准则[9]精确执行强度折减十分困难。文献[12]介绍的强度折减方法仅对描述HB准则的两个材料参数σci和mb进行折减,并简单认为材料折减系数就是强度折减系数。事实上本文方法将证明材料折减系数并非真正意义上的强度折减系数。

对于2002版通用HB准则[9],本文在p-q空间分析了HB曲线上任意点切线与MC准则的关系,推求出HB屈服函数材料参数折减系数和剪切强度折减系数之间的关系,分析了潜入强度折减系数的HB弹塑性模型的计算流程,并对如何在Flac3D平台上二次开发作了介绍。最后对一边坡算例进行了验证。本文方法理论上精确实现了非线性HB强度折减,用户自编程序也容易实现。

2 HB和MC准则在p-q空间的关系

本文讨论的2002版通用HB准则[9]可写为:

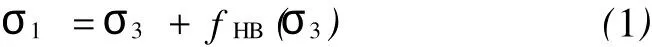
式中σ,1和σ3分别为岩体破坏时最大和最小有效主应力,规定压应力为正;fHB(σ3)=σci[mb(σ3/σci)+ s]α;σci为完整岩石的单轴抗压强度;mb= mie(GSI-100)/(28-14D);s=e(GSI-100)/(9-3D);a=(1/2)+ [e-(GSI/15)-e-(20/3)]/6;mi为完整岩石材料常数,可由室内三轴试验获得;GSI为地质强度指标,反映岩体结构和结构面条件;D为扰动因子,反映岩体因开挖受到的爆破损伤和应力松弛影响程度。

式(1)是岩石常规三轴(σ1>σ2=σ3)试验基础上总结推广至岩体的经验破坏准则[13],在σ1-σ3平面用Lambe不变量p和q可表示为:

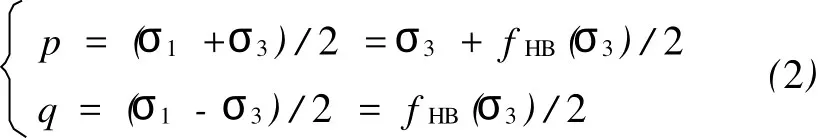
可推导HB准则在p-q平面任意点A(图1)的斜率SHB:

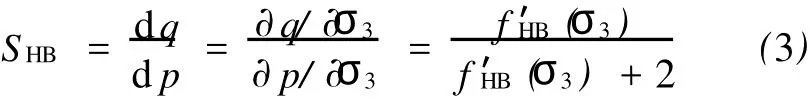
式中,fHB′(σ3)为fHB(σ3)关于σ3的导数,且fHB′(σ3) =amb[mb(σ3/σci)+s]a-1。

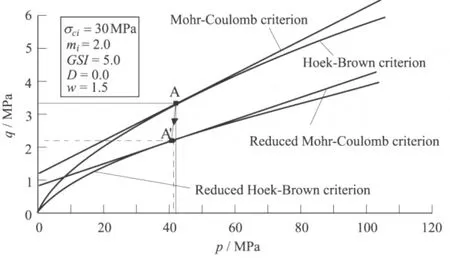
图1 HB和MC准则的p-q关系Fig.1 The p-q relationships fo r the HB and MC criteria

图1中HB曲线上任意点(p,q)的切线方程可用线性MC准则描述。设图1中HB曲线任意点(p,q)对应的MC瞬态摩擦角为φ。而MC准则在σ1-σ3平面上可表示为:

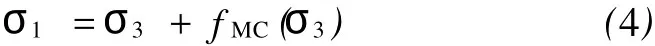
也可用p和q表示式(4),并可推导图1点A的斜率SMC:

HB和MC准则在图1点A等效的条件是SHB=SMC,则联立式(3)和(5)得:

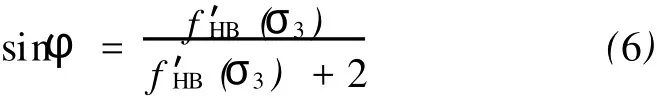
3 HB强度折减方法

3.1 与MC强度折减的关系

郑颖人等[4]对D rucker-Prager屈服函数材料参数项折减,并与MC强度折减系数联系起来,在Ansys程序中进行了强度折减。本文也按此思路推求HB屈服函数材料参数项折减系数与MC强度折减系数的关系,介绍如下。

HB准则用屈服函数可表示为:

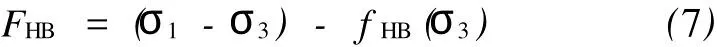
对式(7)中材料参数项fHB(σ3)折减w,则新的屈服函数为:

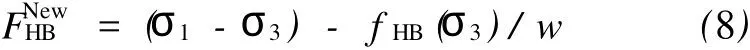
对于式(8),当应力状态处于屈服时有FNewHB= 0,即:

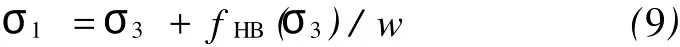
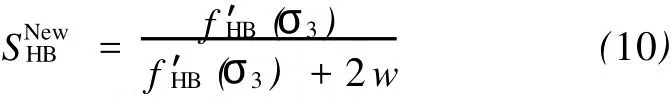
类似地,MC准则也用屈服函数表示。对材料参数项fMC(σ3)折减w后,也可推求图1点A′的斜率:

因图1点A对应的HB和MC屈服函数值均对材料参数项折减了相同系数w,则折减后它们在点A′也完全等效,即SNewHB=SNewMC成立。则联立式

(10)和(11)得:

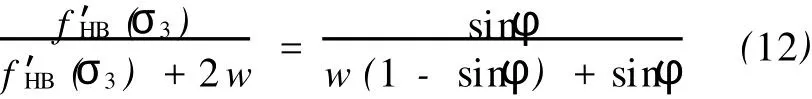
式(12)化简后与式(6)完全相同。

记MC准则描述的切点(图1点A)位置的强度折减系数为Fs。MC瞬态强度参数c和φ折减后为csr和φsr,它们分别对应如下关系:

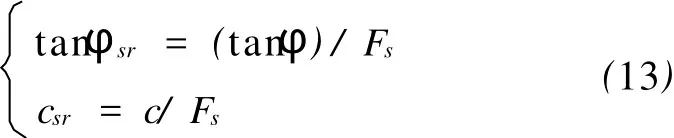
用式(13)对图1点A对应的强度折减,以及对MC准则描述的屈服函数中材料参数项fMC(σ3)折减w后,它们至点A′完全重合的充分必要条件是:p-q平面对应的斜率和截距均相等。

下面先分析p-q平面斜率相等条件。用式(13)对图1点A对应的MC强度参数折减后,类似式(5)可写出点A′的斜率SNewMC:

联立式(11)和(14)得:

式(13)中tanφsr=tanφ/Fs,通过三角函数变换并化简得:

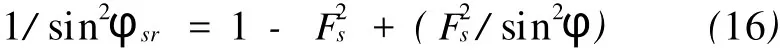
式(15)代入(16)得:

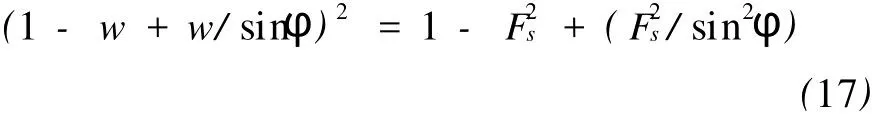
接下来分析p-q平面截距相等条件。可写出MC屈服函数材料项fMC(σ3)折减w后p和q的表达式。则条件p=0对应的截距qw经简单变换可推求:

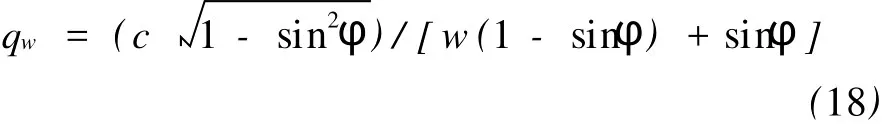
用式(13)对MC强度折减后,可写出p和q的表达式,并可推求相应的截距qsr:

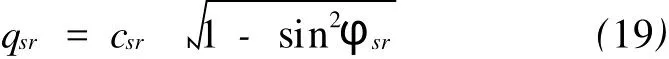
由截距相等条件qw=qsr,联立式(18)和(19)得:

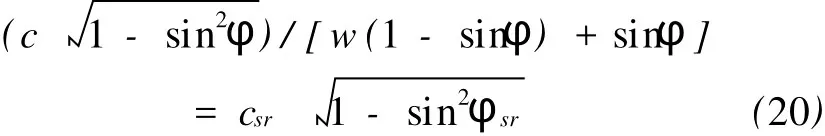
将式(13)代入式(20),化简后同样可得式(17)。

显然,用MC准则描述图1点A位置切线时,对应的瞬态强度参数c、φ折减后以及屈服函数材料项fMC(σ3)折减后,它们在图1点A′完全重合的充分必要条件满足。

将式(6)代入式(17),化简后得:

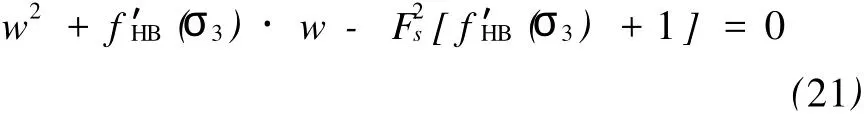
式(21)为关于变量w的一元二次方程。对于HB准则,由于只有当w为正数时才有物理意义,则满足式(21)的解只有:

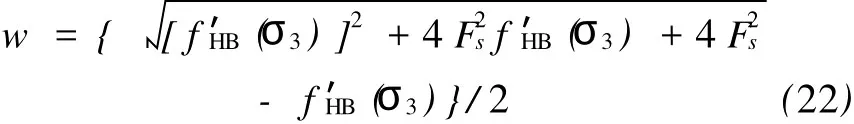
根据目前强度折减法思路,当给定强度折减系数Fs时,用计算模型当前步单元应力代入式(8),可计算出屈服函数值FNewHB。屈服函数值满足FNewHB>0时表明单元发生破坏,需更新当前步单元应力至屈服面,并迭代进行弹塑性分析。实际计算时需通过不断调整Fs,直至计算模型(如边坡稳定性分析模型)处于极限平衡状态,则对应的Fs即为整体安全系数。

3.2 内嵌强度折减系数的HB弹塑性模型

文献[13]介绍了σ1、σ2和σ3主应力空间HB弹塑性增量本构关系。主要假设是σ2方向不发生塑性流动,且塑性应变增量Δεp1和Δεp3假定如下流动法则:

对于式(23)中塑性因子γ的计算,文献[13]提出的弹塑性模型是根据不同应力状态采用不同的流动法则,包括径向流动法则、关联流动法则、常体积流动法则和组合流动法则[13]。本文提出的内嵌强度折减系数的HB弹塑性模型,仍可用文献[13]介绍的方法。对于内嵌强度折减系数的HB弹塑性模型,下面对不同应力状态对应的流动法则及塑性因子的计算进行分析。

(1)径向流动法则

径向流动法则适于多轴受拉应力状态(σ3<0且σ1<0),相应的塑性因子γrf与HB材料参数无关,并用下式计算:

(2)关联流动法则

关联流动法则适于单轴受压邻近区域(σ3≤0且σ1>0)。关联流动法则是取塑性势函数G与屈服函数F完全一致的表达式(即G=F),塑性应变增量的计算用下式计算:

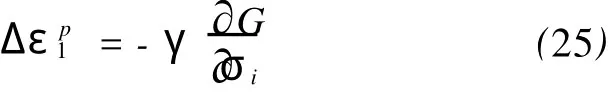
式中,下标i表示在主应力方向的分量,塑性势函数直接用式(8),且式(8)中的w用式(22)代替。

式(25)中的塑性势函数G取式(8)。对式(8)分别关于σ1和σ3求偏导,并将式(25)在σ1和σ3方向的塑性应变增量代入式(23),则可推求关联流动法则对应的塑性因子γaf的表达式:

Pearson相关分析结果显示，干眼仪检测的泪膜脂质层分级与Keratograph 5M眼表综合分析仪测量的NIBUT（f）、NIBUT（av）之间具有相关性（r=-0.145，P=0.011；r=-0.147，P=0.019）。

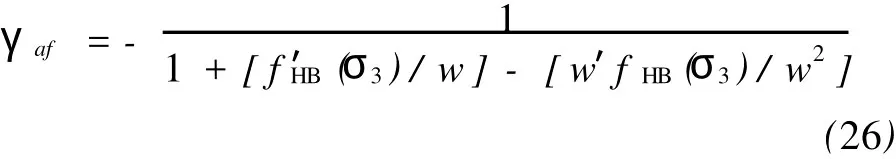
式中,w′为w关于σ3的导数,且(σ3)为 fHB(σ3)关于σ3的二阶导数,且(σ3)=a(a-1) (/σci)[mb(σ3/σci)+s]a-2。

(3)常体积流动法则

当σ3处于较高应力状态时不发生剪胀效应。常体积流动法则适于σ3处于较高应力条件。实际计算时可设定应力值,来控制σ3时采用常体积流动法则,对应的塑性因子γcv则为:

实际上,式(27)与MC弹塑性模型非关联流动法则取剪胀角Ψ=0时完全一致。

(4)组合流动法则

采用组合流动法则的应力条件是0<σ3<σcv3。该应力区间塑性因子γ的计算用关联和常体积流动法则的塑性因子进行线性内插:

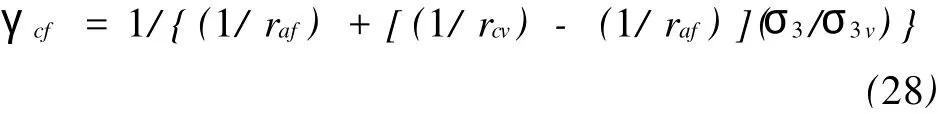
式中,γaf对应关联流动法则的塑性因子;γcv对应常体积流动法则的塑性因子。

需注意的是,式(8)中幂函数底不能为负数。类似文献介绍的方法[14],当单元应力σ3<-sσci/mb时,fHB(σ3)用下式代替:

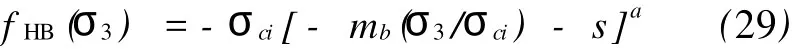
则前述fHB(σ3)关于σ3的一阶和二阶导数相应变为:

由于HB准则具非线性特征,单元破坏时位于屈服面外的应力返回至屈服面时需迭代计算。迭代计算过程出现σ3<-sσci/mb时,也用式(29)～(31)。

3.3 Flac3D平台二次开发

文献[13]提出的弹塑性模型已潜入在Itasca公司开发的Flac3D程序中[14]。需注意的是,本文提出的内嵌强度折减系数HB弹塑性模型,不能直接调用Flac3D程序中的HB模型。但是在Flac3D平台上进行二次开发,对自编用户模型编译生成DLL文件后,可加载到Flac3D程序中。Flac3D平台有关用户模型的开发可参考Flac3D用户手册[13]。下面主要介绍作者在Flac3D平台上开发用户模型的一些体会。

(1)利用Itasca系列程序用户开发共享模版,将ItascasharedmodelsUDM下的udm.zip文件解压至任意用户目录。

(2)将ItascasharedmodelsSource下的userhoek.cpp和userhoek.h两个文件复制至包括udm.zip解压后文件的用户目录。

(3)若系统安装有M icrosoft Visual Basic 2005或以上版本,双击udm.vcp roj文件。在图形窗口左侧udm的Header Files和Source Files位置先移出有关文件。然后在Header Files位置添加userhoek.h,在Source Files添加userhoek.cpp。用户可修改userhoek.h和userhoek.cpp文件名。

(4)在udm属性窗口进行有关设置后,便可以对程序提供的userhoek.h和userhoek.cpp文件中的内容进行修改。修改时需注意符合有关C语言程序编写的要求。按本文介绍的方法适当修改userhoek.h和userhoek.cpp文件中的内容,便可以精确执行内嵌强度折减系数HB弹塑性模型。主要有两点修改:一是添加了用户需输入的强度折减系数Fs;二是屈服函数值和塑性因子计算时涉及Fs处进行了修改。

(5)修改完成后,编译生成DLL文件。然后将相应文件名的DLL文件复制至Itascaflac3d300目录下。具体调用时,在用户的计算模型按如下顺序执行命令并调用文件:

config cppudm(注:必须设置cppudm命令才能加载编译后的用户模型)

model load userhoek.dll(注:加载编译生成的DLL文件,用户可取任意文件名)

model userhoekbrow n...(注:userhoekbrow n为用户在userhoek.h中所取材料模型名称)

p roperty...(注:p roperty后的材料参数中需添加强度折减系数项)

(6)具体的计算模型(如边坡稳定性计算模型)强度折减计算时可采用有关判据[6],通过不断试算强度折价系数Fs,直至计算模型处于极限平衡状态,此时对应的Fs即为整体安全系数。

4 边坡算例

4.1 计算条件

一边坡高度10 m、坡度35°,几何尺寸和单元网格见图2。边坡材料视为均质,且材料基本参数取:E0=410 M Pa,μ=0.3,γ=25 kN/m3,σci=30 M Pa, mi=2.0,GSI=5.0,D=0。在Flac3D中自编FISH程序按前述公式计算得:mb=0.067,s=2.6×10-5, a=0.619。边坡算例仅考虑自重应力场,不考虑地下水水位、地震荷载等条件。沿边坡走向取厚度1 m建立半整体三维模型,模型左右两侧以及边坡走向两侧为法向约束,底部固定。采用二分法[3]调整强度系数Fs,Fs的初始下限和上限分别设为1.0和2.0,当二分法计算过程的上限和下限差低于0.01时计算结束。弹塑性分析最大迭代步数控制为15000步,取默认节点平均内力与最大不平衡力比值的收敛控制精度为1.0×10-5,算例中与流动法则有关的参数σcv3设为0。

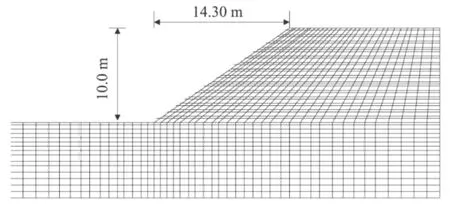
图2 边坡几何尺寸及离散网格Fig.2 Geometry size and grids of the slope

4.2 计算结果

按本文方法计算获得极限平衡状态时边坡塑性应变等值线见图3,边坡位移矢量特征见图4。由图3可以看出,该边坡塑性应变沿坡脚至坡肩已经贯通,并呈近似圆弧的条带状分布。由图4可以看出,边坡潜在运动趋势是边坡中上部靠坡肩部位总体表现为沿滑面下滑,边坡中下部尤其是坡脚部位总体表现为水平外鼓。本文方法较好地揭示了均质边坡潜在破坏具圆弧滑面的破坏模式和运动趋势。计算获得边坡整体安全系数Fs=1.406。

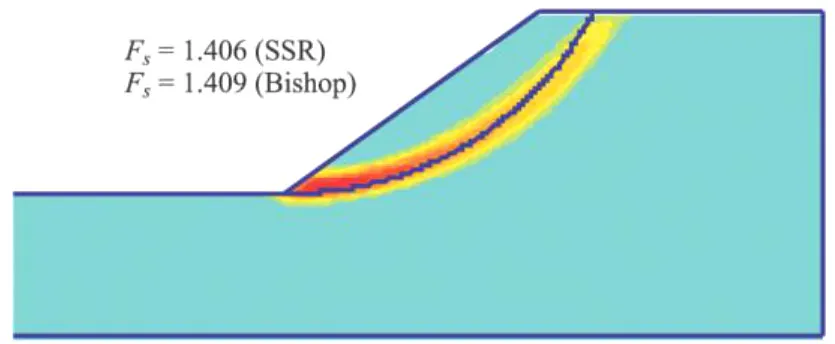
图3 边坡塑性应变分布及Bishop法圆弧滑动面Fig.3 Slope p lastic strain distribution and Bishop slip circle

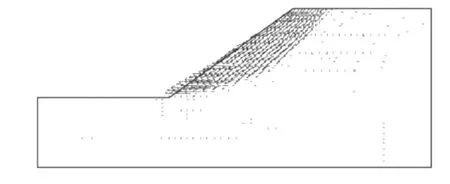
图4 边坡潜在滑动趋势Fig.4 Potential sliding trend of the slope

为了与强度折减法结果对比,也用Slide程序中HB模型作了简化Bishop法计算。Bishop法搜索的最小安全系数Fs=1.409,对应的圆弧滑动面也绘于图3中。对比图3中Bishop法圆弧滑动面与强度折减法预测的滑动带形态和位置可以看出,边坡上部Bishop法圆弧滑动面的位置略浅,但是中下部两种方法对应的滑面位置有很好的一致性。另外,两种方法计算获得的安全系数也近相等,它们之间的差值仅约0.003。

5 结论

(1)节理岩体的抗剪强度具显著的非线性特征,用非线性HB准则能较好地描述其破坏机理。本文在p-q空间推求了HB屈服函数材料项折减系数与剪切强度折减系数的内在关系,分析了HB弹塑性模型中潜入了强度折减系数后的计算流程,介绍了FLAC3D平台上二次开发的主要思路,精确实现了非线性强度折减。本文方法也很容易嵌入用户自编程序。

(2)边坡算例表明,潜入强度折减系数HB弹塑性计算获得的边坡整体安全系数Fs=1.406,简化Bishop法最小安全系数Fs=1.409,它们之间的差值仅约0.003,且计算获得的滑动面形态和位置也有很好的一致性,表明本文方法正确。

(3)与传统的极限平衡法相比,强度折减法不需假设滑面位置和形态以及条分之间力的相互作用关系,但同样可以获得边坡整体安全系数。尤其是根据强度折减极限状态弹塑性分析结果绘制的塑性应变等值线、位移矢量等,能直观地揭示边坡潜在破坏趋势及范围,并为边坡设计加固提供明确的依据。

[1]Zienkiewicz O C,Humpheson C,Lewis RW.Associated and nonassociated viscoplasticity in soil mechanics[J]. Géotechnique,1975,25(4):671-89.

[2]ZHENG Hong,SUN Guan-hua,L IU De-fu.A p ractical p rocedure for searching critical slip surfacesof slopes based on the strength reduction technique[J].Computers and Geotechnics, 2009,36(1-2):1-5.

[3]Daw son EM,Roth W H,Drescher A.Slope stability analysis by strength reduction[J].Géotechnique,1999,49(6):835-840.

[4]郑颖人,赵尚毅,宋雅坤.有限元强度折减法研究进展[J].后勤工程学院学报,2005,21(3):1-6.

[5]Luan M T,Wu Y J,Nian T K.An alternating criterion based on development of plastic zone for evaluating slope stability by shear strength reduction FEM[C].In:Proceedingsof the Sina -Japanese Symposium on Geotechnical Engineering,Beijing, China,2003:181-188.

[6]吕庆,孙红月,尚岳全.强度折减有限元法中边坡失稳判据的研究[J].浙江大学学报:工程科学版,2008,42(1):83-87.

[7]Griffiths D V,Lane P A.Slope stability analysis by finite elements[J].Géotechnique,1999,49(3):387-403.

[8]Duncan J M.State of the art:limit equilibrium and finite-element analysis of slopes[J].Journal of Geotechnical Engineering ASCE,1996,122(7):577-596.

[9]Hoek E,Carranza-Torres C,Corkum B.Hoek-Brow n criterion-2002 edition[C].In Proceedings of the 5th North American Rock Mechanics Symposium and the 17th Tunnelling Association of Canada:NARMS-TAC 2002,Toronto,Canada, eds.R.E.Hammah et al.,267-273.

[10]杨小礼.岩石极限分析非线性理论及其应用[J].中南大学学报:自然科学版,2009,40(1):225-229.

[11]林杭,曹平,赵延林,等.强度折减法在Hoek-Brow n准则中的应用[J].中南大学学报:自然科学版,2007,38(6):1219-1224.

[12]吴顺川,金爱兵,高永涛.基于广义Hoek-Brow n准则的边坡稳定性强度折减法数值分析[J].岩土工程学报,2006,28 (11):1975-1980.

[13]Cundall P,Carranza-Torres C,Hart R.A new constitutive model based on the Hoek(Brown Criterion[C].In Proceedings of the 3rd International FLAC Symposium,Sudbury,Ontario, Canada,October 2003,FLAC and Numerical Modeling in Geomechanics,eds.R.Brummer et al.,2003:17-25.

[14]Itasca Consulting Group.Theory and background[M].Minnesota:Itasca Consulting Group,2002.

NON-L INEAR HOEK-BROWN STRENGTH REDUCTION TECHNIQUE

FU Wen-xi1,Wang Qi-hong2,L IU Chang-w u1
(1.State Key Laborato ry of Hydraulic and Mountain River Engineering,School of Water Resource and Hydropower, Sichuan University,Chengdu 610065,China;2.Engineering Institute of HydroChina Xibei Engineering Co rpo ration,Lanzhou 730050,China)

To exactly imp lement the non-linear Hoek-Brow n(HB)strength reduction,firstly,the HB criterion was connected w ith the Mohr-Coulomb(MC)criterion using the slopeof an arbitrary point at the p-q curve.The relationship between thematerial strength reduction factor incorporated in the HB yield function and the strength reduction facto rwas derived.After analyzing the computational p rocedure fo r the HB elasto-p lastic model w ith a strength reduction factor,autho rs introduced main development steps to imp lement the non-linear strength reduction on the Flac3D p latform.In the end,a slope examp le was analyzed using the p resent HB strength reduction technique and the simp lified Bishop method.The results indicate that the geometry shape and position of the sliding plane and the co rresponding safety facto r calculated using the non-linear HB strength reduction method are consistent with those obtained using the simp lified Bishop method.

Hoek-Brow n criterion;Mohr-Coulomb criterion;strength reduction;safety facto r

TU 457

:A

1006-4362(2010)02-0082-06

符文熹(1972- ),男,四川渠县人,博士,副教授,研究方向:岩土工程。

2010-03-22改回日期:2010-04-21

国家自然科学基金项目(编号:40972190);国家973计划项目(编号:2010CB226802)