蚁群算法在车间调度问题中的应用

张晓玲，何彩香，陈建华

（大理学院数学与计算机学院，云南大理 671003）

蚁群算法在车间调度问题中的应用

张晓玲，何彩香，陈建华

（大理学院数学与计算机学院，云南大理 671003）

提出用蚁群算法求解车间调度问题。车间调度问题是典型的非确定性多项式时间难问题，蚁群算法是一种分布式进化计算方法，具有鲁棒性，正反馈，并行性等特点，而且算法简单。给出了用蚁群算法求解车间调度问题的流程，并且用经典的J SP的样例对算法进行了测试，实验结果表明用蚁群算法可以求解得到车间调度问题的最优解或近似最优解。

蚁群算法；车间调度问题；信息素；

0 引言

车间调度问题（Job-Shop Scheduling Problem，JSP）是在经典的调度理论中所描述的最难的组合问题中的一种，是典型的非确定性多项式时间难问题（NP）。已经有许多方法用来解决JSP，包括线性规划、神经网络〔1〕、遗传算法〔2〕、禁忌搜索〔3〕、粒子群算法〔4〕和蚂蚁系统等等。

蚁群算法（Ant Colony Algorithm，ACA）是由意大利学者M.Dorigo在20世纪90年代提出的一种模仿自然界蚂蚁群的觅食行为的一种分布式进化计算方法，具有并行性、算法简单和求解效率高等特点。蚁群算法模拟了自然界蚂蚁寻找从蚁巢到食物源的最短路径并找到回蚁巢路径的机制，蚂蚁之间通过一种信息素（“激发工作”，stigmergy）〔5〕来相互交流信息。蚂蚁在移动的过程中，会在经过的路径上散发信息素，蚁群通过感知路径上的信息素进行通信，个体之间并不直接进行交互，而是通过改变它们共同存在的环境进行交互，个体又通过对环境的改变去影响其它个体的行为，从而形成了一种正反馈机制。长度越短的路上，经过的蚂蚁越多，聚集的信息素也越多，蚂蚁趋向于选择信息素多的路径移动。通过这种机制，经过一段时间后蚂蚁最终能够发现最短路径。蚁群算法已经被成功地应用于解决组合优化问题，如：旅行商问题（Traveling Salesman Problem）〔6〕，二次分配问题（Quadratic Assignment Problem），JSP等。本文讨论的是用ACA求解JSP。

1 车间调度问题

1.1 问题的描述 JSP问题可以描述为：有n（n≥3）个加工顺序不同的工件要在m（m＞2）台机器上完成加工。

已知：工件集J=｛J1，J2，…，Jn｝，Ji为第i个工件，i= 1，2，…，n；机器集M={M1，M2，…，Mm}，Mj为第j号机器，j=1，2，…，m；每个工件有k道工序，每道工序要求在不同的机器上加工，并且预先已经定义了每个工件在m台机器上的加工顺序，uij表示工件i在机器j上加工，工序序列集O={uij｜i∈〔1，n〕，j∈〔1，m〕｝，其中n为工件的数目，m为机器的数目。

每个工件使用每台机器的时间矩阵T，tij∈T为第i个工件Ji使用第j台机器的时间。tij=0表示工件Ji不使用机器Mj。

JSP问题满足以下约束：①每个工件使用每台机器不多于1次；②不同的工件的工序之间没有先后约束；③每台机器一次只能加工一个工件，并且工序一旦进行不能间断；④工件加工过程中没有新工件加入，也不临时取消工件的加工。

cij=cik+Tij是工序uij相对于关系uik→uij的完整的执行时间，调度目标：求出可行的工序的加工序列，使其最后一道工序的最大完工时间Cmax最小。

1.2 JSP的表示 可以用析取图D=（N，A，B）来表示JSP问题，N是所有结点的集合，每个结点对应一个工件的一个工序uij，并且N=m·n。A是工件使用机器的加工顺序的有向弧的集合。B是连接在同一台机器上处理的不同工件工序的无向弧的集合。为了确定先对哪个工件进行加工和什么时候加工结束，需要设置一个初始结点O0和调度结束的结点O10。以3个工件3台机器的问题作为例子。如图1。

图1 3／3／G／Cmax JSP的表示图

在图1中，0=O0，10=O10，1=u12，2=u13，3= u11，4=u21，5=u22，6=u23，7=u31，8=u33，9=u32，结点1旁边的（1，2）5表示工件1的第一道工序在机器2上处理，处理时间为5，图中除与O0和O10相连的有向弧，其它的有向弧表示同一个工件的加工顺序，工序必须按照该顺序进行加工，其它的为无向弧。每一行加工一个工件，123加工工件1，456加工工件2，789加工工件3。每个工件只能使用每台机器一次，有m台机器，则每个工件就有m道工序。因此求解JSP就变成在满足约束的前提下，求得上图中结点的一个序列，例如{4，1，7，8，2，3，5，9，6｝，求出在每台机器上加工完毕所有的工件的最后一道工序时的最大完工时间，求解目标：求出最大完工时间最小的序列，即为调度的最佳序列。

2 ACA求解JSP

根据图1，ACA求解JSP的基本工作过程如下：

由于在整个工件调度的过程中添加了一个开始的结点O0和结束的结点On+1，因此所有的蚂蚁从结点0（工序0）出发，最后到达的结点是结点10。设集合Gk是没有访问过的结点的集合，Sk表示根据约束规则下一步允许访问的结点的集合，还需要一个禁忌表J k，存放已经访问过的结点。在上面的例子中，Gk={1，2，3，4，5，6，7，8，9}，Sk={1，4，7}。首先蚂蚁分布在0结点，然后每个蚂蚁根据状态转移规则选择下一个结点，蚂蚁倾向于选择那些加工时间较短且信息素强度较高的路径，图中的每个弧表示节点间信息素的量和启发式距离的一对值 {αij，Tij}，Tij通常为对工件j的第i步工序的加工时间。每选择一个结点，该结点就被追加到禁忌表Jk中并从Gk中删除：如果被选的结点不是工件的最后一步，那工件中紧邻的下一个结点就会被加入到Sk中。单个的蚂蚁在遍历过程中根据信息素局部更新规则在路径上释放一定数量的信息素，同时蚂蚁经过的路径上的信息素随着时间的推移而蒸发。当所有的蚂蚁都完成了它们的遍历过程之后，Gk=ø。最后禁忌表中得到的结点的排序序列就是蚂蚁k找到的解。此时可以计算出此次迭代的最小的最大完工时间，再应用信息素全局更新规则对获得最小的最大完工时间的蚂蚁所经历的边上的信息素进行更新。此后算法反复迭代直至满足终止条件后结束。可见，蚁群算法的求解过程主要由三个规则控制，即状态转移规则，信息素全局更新规则和信息素局部更新规则。下面将对这三个规则进行说明。

2.1 状态转移规则 ACA中的状态转移规则（又叫做“伪随机比例规则”），“伪随机比例规则”为在保持探索（exploration）一条新的边和利用蚂蚁所积累的搜索经验开发（exploitation）一条边之间的平衡提供了一种直接的方式，状态转移规则如下：位于结点r的蚂蚁k使用以下的规则（1）选择结点s为下一个要访问的结点

在（2）中，τ是信息素，η是启发函数，η（s）=1/T（s）是在结点s的工序在机器上的处理时间的倒数，Sk是蚂蚁k还没有访问过的结点的集合，而β＞0是一个参数，用来定义信息素和时间之间的相对重要性。q是一个均匀分布的随机数，q∈〔0，1〕，0≤q0≤1是自定义的一个参数。S是根据以下的概率公式（3）计算得来的随机变量。

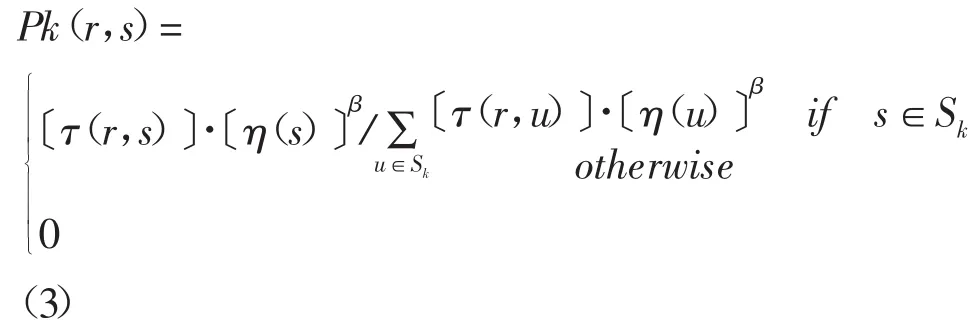
伪随机比例规则使得蚂蚁倾向于选择加工时间短且信息素强度浓的路径。参数q0决定了“探索”和“开发”之间的相对重要性。当位于结点r的蚂蚁k要选择下一个将要访问的结点时，它选择一个随机数0≤q≤1，如果q≤q0则按照式（1）根据启发信息和信息素强度取最好的边，否则，按照式（2）随机比例规则选择下一条要移动的边。

2.2 信息素全局更新规则 在ACA中，当所有的蚂蚁都访问完所有的结点以后，只有那些属于最小的最大完工时间的边上的信息素才被得到增强，信息素全局更新规则的使用使算法的寻优过程更具有指导性：最小的最大完工时间寻找始终是在当前找到的最小完工时间的附近进行。按以下的公式（4）对最小的最大完工时间的边上的信息素进行更新。

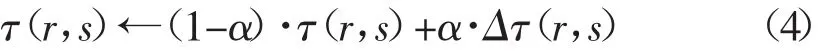
其中，

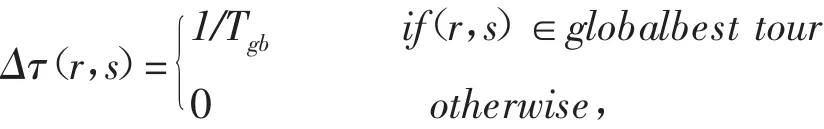
0＜α＜1是信息素衰减系数，而Tgb是蚂蚁k在本次循环中找到的最小的最大完工时间。

2.3 信息素局部更新规则 单个的蚂蚁在遍历过程中按照式（5）信息素局部更新规则对它所经过的边上的信息素进行更新。

0＜ρ＜1是信息素挥发系数，τ0是预先设置的信息素的初始值，信息素局部更新规则使得被蚂蚁经过的路径减少了一部分信息素，使得这些边被后来的蚂蚁经过的可能性减少，增强了算法的“勘探”能力，从而有效的避免算法进入停滞状态（所有的蚂蚁收敛到同一解）。

2.4 ACA求解JSP的算法描述 假设以下是求n个工件m个机器的JSP问题，蚂蚁的个数为工件的个数，则求解JSP的ACA流程图。见图2。

描述如下：

步骤1：初始化算法的各项参数：初始信息素τ0，ρ，β，α，蚂蚁个数n，最大迭代次数，工件数n，机器数m等等；

步骤2：把n只蚂蚁放在开始结点0上；

步骤3：每一只蚂蚁应用伪随机比例规则（2）和（3）选择下一个要访问的工序，并应用信息素局部更新规则（5）更新蚂蚁所经过的路径上的信息素；

步骤4：所有的蚂蚁都到达了最后结束的结点n+l，每只蚂蚁就构建了JSP的一个解，计算出此次迭代中所有蚂蚁的最大完工时间，求出其中完工时间最小的值，应用信息素全局更新规则（4）更新最小的最大完工时间的边上的信息素；

步骤5：判断是否已经满足结束的条件，如果满足，则输出最小的最大完工时间的值，否则跳转到步骤2继续执行下一次的迭代。

3 实验仿真与结果分析

本文采用了4个经典的JSP问题：FT03，FT06，LA06和LA07的测试用例来说明用ACA求解JSP的优势。

3.1 实验仿真 样例的规模不同，ACA在求解时候的参数的设置也不同，具体的参数设置见表1。

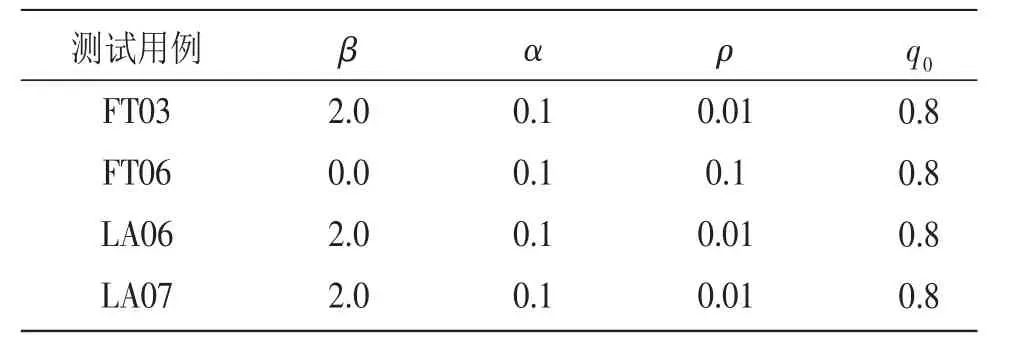
表1 蚁群算法求解JSP的参数设置

为了降低由于系统和统计的误差，对求解的每个用例都进行了10次的仿真，实验结果是10次仿真的统计值（平均最优值和方差等）。

3.2 结果比较 表2给出了使用ACA求解4个样例的结果，由于这里给出的数据是基于10次测试的平均值，因此可能会有小数。同时，表中的“OPT”一列是样例的已知的最优解。从表2的数据中可以看出，采用ACA来求解JSP具有非常明显的优势。ACA能够很快的找到问题的最优解。为了能更加直观地反映算法的优势，图3给出了FT06，LA06和ABZ6在优化问题的时候的进化特征曲线。

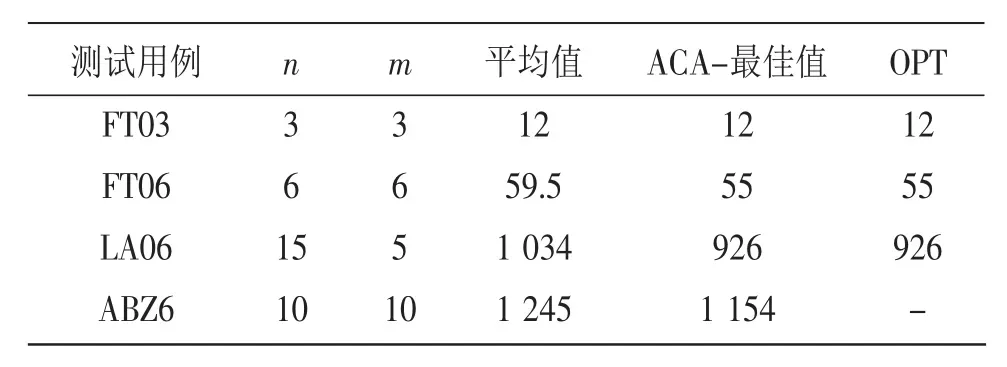
表2 基于表1的参数设置的ACA求同JSP的平均结果

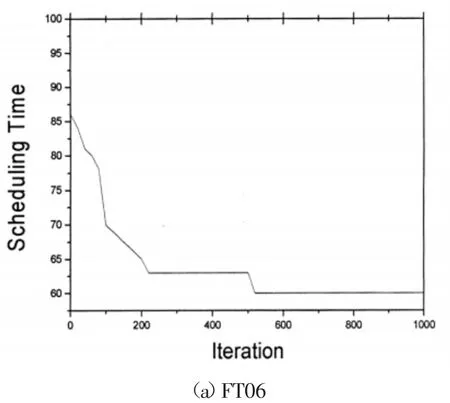
图3 ACA求解不同JSP的进化特征曲线图

在图3中可以看出ACA在求解JSP（FT06，LA06和AB Z6）时用了1 000次迭代的收敛速度，一般都在500次迭代左右就可以收敛（ABZ6问题的最优解出现在每次迭代中）。虽然表2和图3都体现出了A C A在求解J S P时的高效性，当然A C A在求解JSP时也存在工件数目越多算法的时间复杂度越大等问题。

对于ACA求解复杂的J S P的时间消耗，还需要对A C A进行改进或融入其它的一些算法，以使算法能够在求得最优解的基础上时间消耗最小。

4 结束语

针对ACA求解JSP，对该算法的基本原理进行了阐述并且给出了具体的实现方案，最后还通过典型的JSP测试样例进行实验仿真，实验结果证明了该策略不但在收敛速度上而且在求解精度上都有很大的优势。

〔1〕唐大志.用Hopfield神经net解决作业调度问题〔J〕.辽宁工程技术大学学报，2004，23（S）：88-90.

〔2〕李胜辉，李莹.遗传算法与人工免疫算法对车间调度问题求解〔J〕.计算机应用研究，2009，26（8）：2928-2930.

〔3〕李俊清，潘全科，王玉亭，等.块邻域结构的禁忌搜索算法在车间调度问题中的应用〔J〕.机床与液压，2009，32（11）：173-188.

〔4〕张长胜，孙吉贵，欧阳丹彤，等.求解车间调度问题的自适应混合粒子群算法〔J〕.计算机学报，2009，32（11）：2138-2145.

〔5〕Dorigo M，Stitzle T.Ant Colony Optimization〔M〕.MA：MITPress，2004.

〔6〕张晓玲，黄力.融入遗传算子的蚁群算法求解TSP问题〔J〕.广西民族大学学报，2009，15（3）：81-87.

Ant Colony Algorithm for Solving Job-Shop Scheduling Problem

ZHANG Xiaoling,HE Caixiang,CHEN Jianhua
（College ofMathematics and Computer Science，DaliUniversity,Dali,Yunnan 671003,China）

This paper proposes Ant Colony Algorithm（ACA）to solve Job-shop Scheduling Problem（JSP）.Job-Shop scheduling problem is a typical NP hard problems,ant colony algorithm is a distributed evolutionary computation methods,The main characteristics of this algorithm are robustness,positive feedback,parallelism,and simple.In this paper,the flow of ant colony algorithm used to solve Job-shop scheduling problem is given,the numerical experiments of ACA were implemented in a small JSP, the experimental results show that the ant colony algorithm can be used to solve job shop scheduling problem and the optimal solution or near optimal solution can be achieved.

Ant Colony Algorithm;Job-Shop Scheduling Problem;pheromone;

TP18

A

1672-2345（2010）10-0010-05

云南省教育厅科研基金资助项目（2010Y349）

2010-04-09

2010-05-20

张晓玲，讲师，主要从事进化计算的研究.

（责任编辑 董 杰）