Leslie型双时滞捕食系统的Hopf分支

崔淑莉,王福

(石河子大学师范学院数学系,石河子 832003)

Leslie型双时滞捕食系统的Hopf分支

崔淑莉,王福

(石河子大学师范学院数学系,石河子 832003)

以滞量τ=σ+β为分支参数,讨论了一类具有双时滞的Leslie型捕食者-食饵系统的正平衡点的稳定性及局部 Hopf分支的存在性,得到存在一个τ0,当τ∈[0,τ0)时,正平衡点是渐近稳定的,当τ>τ0时,正平衡点是不稳定的,而τ0是该系统的 Hopf分支值。

时滞;捕食系统;稳定性;Hopf分支

Abstract:This paper considers the stability of the positive equilibrium and the existence of local Hopf bifurcation for a Leslie type predator-prey system with two delays by choosing the delayτ=σ+βas a bifurcation parameter.There exists aτ0,such that the positive equilibrium is locally asymptotically stable whenτ∈[0,τ0),and unstable whenτ>τ0,and the system undergoes a Hopf bifurcation at the positive equilibrium when τ=τ0.Certain known results are improved.

Key words:delay;predator-prey system;stability;Hopf bifurcation

种群动力学是生物数学中应用最多的一个分支,而捕食-食饵系统又是种群动力学研究的重点。因此,许多学者对捕食-食饵系统进行了研究[1-11]。本文考虑以下具有双时滞的Leslie型捕食者-食饵系统:

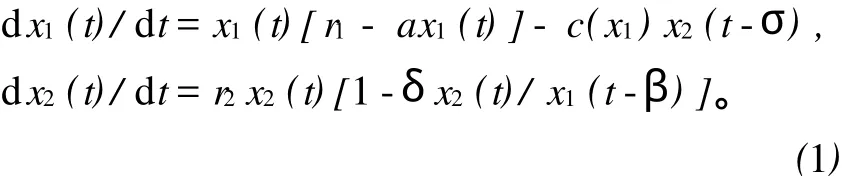
上式中:r1、r2、a、δ是正常数,x1(t)和 x2(t)分别表示食饵种群,捕食者种群在时刻 t的密度;食饵种群x1(t)遵循Logistic增长,r1是食饵种群的内禀增长率,r1/a为食饵种群的容纳量;r2是捕食种群的内禀增长率,x1/δ为捕食种群的容纳量,与食饵种群的大小成比例,δ为食饵转化成捕食者的数量;σ>0,β>0分别表示追捕时间和捕食者的成熟期;c()为功能性反应函数,满足 c(0)=0,′)>0,存在常数k使得)=k。显然,捕食系统的

本文讨论系统(1)的正平衡点的稳定性,并以滞量τ=σ+β为参数,应用 Hopf分支理论研究系统(1)的周期解,得到了正平衡点稳定和发生 Hopf分支的充分条件。这在理论和实际上都有重要的意义。

1 正平衡点的稳定性与Hopf分支

3 结语

本文分析了一类具有双时滞的Leslie型捕食者-食饵系统,讨论了正平衡点的局部稳定性及Hopf分支的存在性。证明了在条件(I)、(Ⅱ)下当时滞τ=σ+β适当小时,正平衡点是局部渐近稳定的,随着时滞的增加,正平衡点由稳定变为不稳定,系统(1)在正平衡点附近发生 Hopf分支,产生了周期解。这表明时滞的引入或时滞的过大将破坏系统的稳定性,是“有害”时滞。

[1]林宏康,谢向东.一类Leslie模型的定性分析[J].数学研究,1996,30(3):308-311.

[2]段文英.关于具时滞的捕食-被捕食系统的稳定性与Hopf分支[J].生物数学学报,2004,19(1):87-92.

[3]刘建芳,陈东青,冯元辉.第IV类时滞捕食系统的 Hopf分支[J].军械工程学院学报,2008,20(2):76-78.

[4]张建明,骆桦,周小红.时滞 Leslie-Gower捕食者-食饵系统 Hopf分支的存在性[J].浙江理工大学学报,2008,25(1):95-98.

[5]Liu Z H,Yuan R.Stability and Bifurcation in a Harvested One-predator-two-prey Model with Delays[J].Chaos Soli Frac,2006,27(5):1395-1407.

[6]Huo H F,Li W T.Periodic solutions of delayed Leslie-Gower predator-prey model[J].Applied Mathematics and Computation,2004,155:591-605.

[7]Song Y,Wei J.Local Hopf bifurcation and global periodic solutions in a delayed predator-prey system[J].J Math Anal Appl,2005,301:1-21.

[8]邹娓,谢杰华.具有时滞和比率的 Holling-III Leslie系统的 Hopf分支[J].南昌工程学院学报,2007,26(6):37-40.

[9]刘志军.一类具反馈控制单种群时滞模型的 Hopf分支[J].湖北民族学院学报:自然科学版,2005,23(3):213-215.

[10]宋永利,韩茂安,魏俊杰.多时滞捕食-食饵系统正平衡点的稳定性及全局 Hopf分支[J].数学年刊:A,2004,25(6):783-790.

[11]李小玲,胡广平.多时滞食饵-捕食系统平衡点的稳定性和周期解的存在性[J].西北师范大学学报:自然科学版,2009,45(3):1-3.

[12]Freadman H I.Strea Hari Rao V.The treade-off between mutual interference and time lags in Predator-Prey System[J].Bull Math Biol,1983,45:991-1003.

[13]Hale J K.Theory of Functional Differential Equations[M].New York:Spring,1977.

Hopf Bifurcation of Leslie Type Predator-Prey System with Two Delays

CUI Shuli,WANG Fu
(Department of Mathematics,Teachers College,Shihezi University,Shihezi 832003,China)

O175.7

A

1007-7383(2010)05-0655-03

2010-03-10

崔淑莉(1976-),女,讲师,从事应用微分方程研究;e-mail:cuishuli㊦tea@shzu.edu.cn。