描述微观高速过程的模糊图

2010-10-28邱文兵殷保祥刘军岭

石河子大学学报（自然科学版） 2010年5期

关键词：性态费曼重整

邱文兵,殷保祥,刘军岭

(石河子大学师范学院物理系,石河子 832003)

描述微观高速过程的模糊图

邱文兵1,殷保祥1,刘军岭1

(石河子大学师范学院物理系,石河子 832003)

对于费曼图导致紫外发散的出现,且不能计算其电磁质量和重整化导致的电荷改变量的问题,采用模糊图论描述微观高速领域,从而既可消除紫外发散,又能计算电磁质量和重整化导致的电荷改变量。结果表明:真空作用导致的电子质量和电荷的改变量都很小,分别为0.3%、0.026%。利用模糊图计算了电子传播子的一级修正形式,发现该形式不同于通常的形式,不需要电荷重整化,同时也避免了红外发散,对S矩阵元的修正是微小的辐射修正。

费曼图;模糊图;微观高速过程;紫外发散;电磁质量;电荷;改变量

Abstract:Since it leads to ultraviolet divergences and cannot calculate the change quantities of the mass and charge of electron in renormalization process,fuzzy graph is used to describe microcosmic fast-speed domain in this paper.Thus,on the one hand,ultraviolet divergences can be canceled;on the other hand,electronic electromagnetic mass and charge change can also be derived.The results indicate that these two changes are both very small respectively with number value 0.3%and 0.026%.The form of the second order approximation for the propagator of electron is calculated in fuzzy Feynman diagram,which is different from conventional form.The renormalization of charge is no longer necessary;at the same time,ultra-red divergences are also avoided.The correction to S matrix element is small radiative correction.

Key words:Feynman diagram;fuzzy graph;ultraviolet divergences;microcosmic fast-speed process;electromagnetic mass;charge change

量子场论面临的发散困难有:跃迁振幅中的紫外发散、真空涨落发散、真空自能发散(涉及到宇宙学常数问题)等等。目前的处理方案有重整化理论、超对称理论等。重整化理论不适用于量子引力,并且其处理方式(维数正规化的积分规则)是人为的规则;超对称理论的波色子(费米子)与其超对称伴粒子各自的贡献是无穷大,这是无意义的:重整化理论、超对称理论处理跃迁矩阵元中的紫外发散有效,对于解决有效计算真空涨落、真空自能等问题则显不足。所以探索一种能统一处理各种场论发散和问题、并且在计算过程中也不产生无穷大的新理论方案是有意义和必要的。

现有理论认为点模型是场论发散产生的根源,但点模型改造为弦模型后仍然导致发散,仍需要引入超对称以解决无穷大。所以,点模型是场论发散的根源还是值得探讨的。本文认为场论采用点模型是对场量子的质心运动的描述,并非是把粒子视为没有大小的点,这也是点模型场论可用来描述复合粒子场论的原因。值得注意的是,场量子理论凡涉及到真空处时总遇到发散困难,例如真空涨落发散、真空自能发散、跃迁矩阵元紫外发散等等,这似乎预示:场论发散的根源在于现在的场论概念不适用于真空领域。“真空工程”[1]是个真空问题,所以探索有效自洽描述真空的理论是有实际意义的。

本文从图论角度入手考虑思路,量子场论在一定意义上可以视作费曼图的集合,可以不依赖场论的具体形式而独立地发展费曼规则[2]。然而,费曼图会导致紫外发散的出现,说明费曼图并不是正确描述微观高速真空领域的图论,虽然有所谓的重整化等定论式的方法[3～7]。从数学的观点看,费曼图就是经典数学的普通图论,而除了普通图论,还有模糊数学的模糊图论[8～11]。

1 模糊图

图论可用来描述事物间的关系。根据模糊数学,事物间的关系有本质上清晰、确定和明了的,称为清晰关系。清晰关系用普通图描述,也有本质上不确定和不明了的关系,只能考虑有这种关系的(隶属)程度,用位于闭区间[0,1]里的隶属函数值来量度这种关系的(隶属)程度,这种关系称为模糊关系,模糊关系用模糊图描述。

一个普通图就是由若干线连接若干点而成的网络结构(图1a),其中的每个点称为顶点,可代表某一个具体事物,而每条线称为一个边,可代表某一个清晰关系。一个普通图可表示为 G=G(V,E),其中V、E分别表示图中所有顶点、边的集合V={v1,v2,v3,v4,v5}、E={e1,e2,…,e9}。若对普通图 G(V,E)的每一边赋予一个位于闭区间[0,1]里的实数(图1),这个数就是一个模糊关系的隶属函数值(隶属程度),此时每一边代表一个模糊关系,则普通图就变为一个模糊图(图1b),可表示为 ~G=~G(V,E)。其中,

1)对于图中每对顶点,如果最多仅有一边与之对应,则 G为简单图,如图1a。

2)若对图的边指定方向,则称此图为有向图;否则,称为无向图,如图1。

3)若对于模糊图中每一个边,其隶属度值都为1,则模糊图 ~G即成为普通图G。所以,模糊图是普通图的改造、发展和推广,普通图论只是模糊图论的特例。

下文采用自然单位制和Pauli度规。

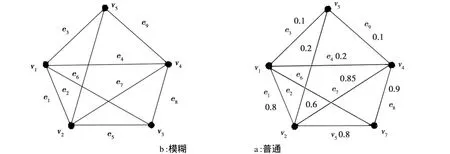
图1 简单、无向图Fig.1 Simple non-directional graph

2 描述微观高速过程的模糊图论的形式及其传播子规则

如果用模糊图描述微观高速过程,需要作如下的观念改变:原来认为在两作用顶点之间有某种清晰的、确定的、分明的场传播关系和性态(传播子),实际上根本不确定,它们带有相当大的模糊性(不同于随机性),可用隶属函数值μ来表示(图2),这里μ∈[0,1]。图2中 G为普通图,即费曼图,~G为模糊图。

对于¯G图中μ4所对应的那个电子传播,以前认为在顶点 v1、v2之间有 SF(k)这样一个确定的传播性态联系,但现在应该认为两顶点间的传播性态联系实际上并不是那么确定,而是本质上就有些模糊,它只是大概为或者近似于SF(k),近似程度用隶属函数值μ4表示,即此电子的传播性态(以大小为μ4的近似程度或隶属程度)近似于 SF(k),也可以说成:传播性态近似于 SF(k)的隶属度为μ4。按模糊理论,这种场传播性态的模糊性应该理解为场的一种本性。由于场传播性态只是以一定大小的程度近似为SF(k),所以场贡献的有效传播子应该取形式μ·SF(k),这就是模糊图的传播子规则(其他规则不变)。

图2 反应过程e-+e-→e-+e-的费曼图和模糊图Fig.2 The diagrams describing the reaction course e-+e-→e-+e- Gis a common graph(Feynman diagram),and is a fuzzy graph)

下面讨论模糊图的每一内线μ应怎样赋值。

在费曼图中紫外发散总是出现于有真空场的地方,紫外发散与真空场密切相关。这似乎预示着传统的关于真空场的观念是存在问题的。费曼图赋予真空场一个绝对确定的传播性态,问题可能就出在传播子的绝对确定性上。因此,模糊图中就认为真空场的传播性态实际上根本不确定,它们带有相当大的模糊性,用隶属函数μ来表示其模,真空场传播子应取为μ·SF(k),这里μ必须满足0≤μ<1。而对于非真空场,它从没有带给场论任何困难,说明关于非真空场的观念不存在问题,不必要改变其物理概念,其传播性态仍是绝对确定的(μ=1),其传播子形式取为μ·SF(k)=1·SF(k)=SF(k)。于是,在模糊图¯G中,有μ4<1,μ5<1,μ1=μ2=μ3=μ6=μ7=μ8=1,这样,在模糊图中真空场的传播性态是模糊性的,这是真空场的本性,是真空场固有的。因此认为:真空场的传播性态是完全确定的,这可能就是“费曼图会导致紫外发散”的深刻原因。

需指出的是,上述只是以真空电子场为例说明真空场观念的改变,它对于任何其他真空场都成立。对于任何真空场,例如电子场、夸克场、中间波色子场等,都有μ<1;对于任何非真空场,都有μ=1。下文用μ·S(k)和S(k)分别代表任何真空场、非真空场的传播子。通常,树图不包含真空场,树图中的传播子都是S(k)。但是,圈图含有真空场,圈图中除了含有 S(k)外,也必包含有μ·S(k)。

这样,如果为每条真空场内线赋予一个适当的隶属函数值,则模糊图将能够给出有意义(有限)的结果——格林函数、S矩阵元、电磁质量δm等。即使我们能够获得收敛的跃迁矩阵元,质量、电磁流的重整化仍是必要的(分别考虑绝热假设、规范不变性的要求[11,12])。这里的重整化运算中不再是无穷大减无穷大,而是有限量减有限量。

最后,考虑真空场隶属函数μ的可能的、具体的数学形式,假设:

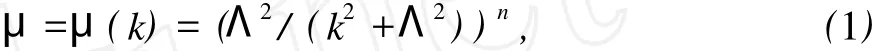
其中 k2=kμkμ≥0,kμ代表真空场量子的4-动量。假设这个形式对于任何真空场的传播子都适用。n应取尽可能小的自然数,要满足使得各种相互作用过程都不出现发散的要求。为此,取 n=3比较合适,因为可以验证:当考虑了隶属函数μ中包含的内部动量后,模糊图的表观发散度为 D′=D-6Iv<0(D是不考虑隶属函数因子而按通常费曼图中方法计算出的表观发散度,Iv是所有真空场内线的条数),不再导致发散。Λ是一个由实验确定的常数参数,对于任何真空场都不变,可以视作截断频率,满足

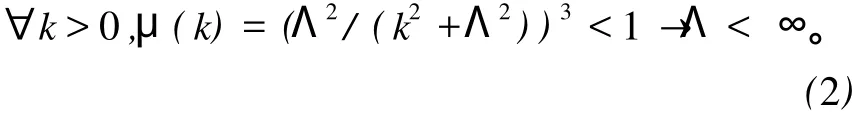
上述理论形式满足相对论不变性。

3 参数Λ的确定及几个具体应用的计算

3.1 真空电磁场导致的顶角修正

下面讨论电子在弱电磁场(k1→0)中散射的顶角修正,如图3所示。

其中m0为电子的实验质量。

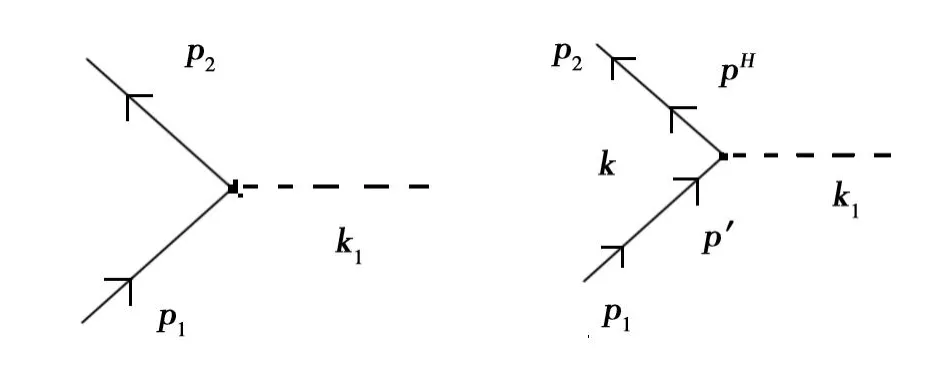
图3 弱电磁场(k1→0)中电子散射的顶角修正.3 The correction to the vertex angle for electron scattering in weak electromagnetic field

图3 a贡献的顶角是γμ,图3b图贡献的顶角修正是Λ(2)μ(p1,p2)。与通常理论不同,这里的顶角修正是一个有限量。因为电子为弱电磁场(k1→0)所散射,电子近似自由,故有:

3.2 电子电磁质量的计算

图4是电子自能图,这是一个模糊图,其中的虚线代表真空电磁场,其隶属函数μ(k)<1。

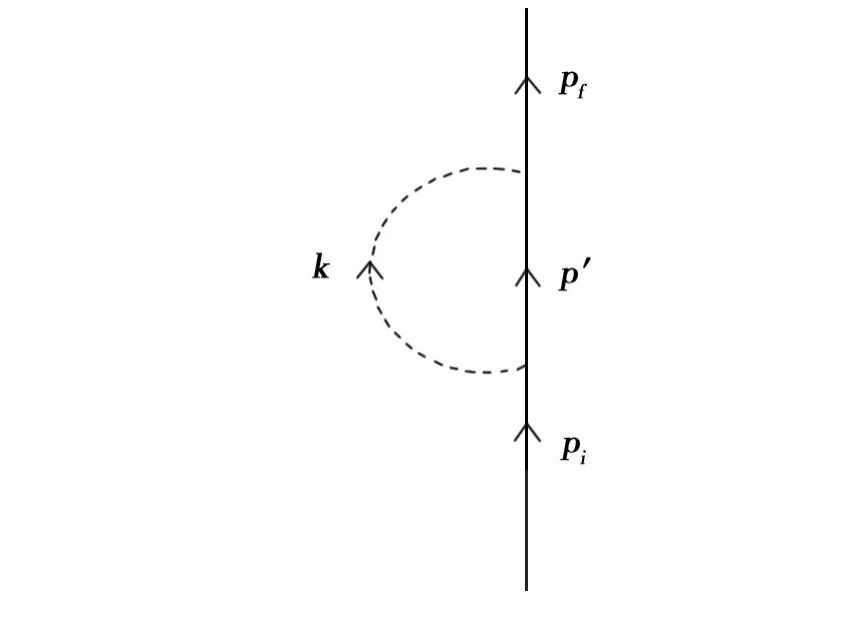
图4 电子的自能Fig.4 The self-energy diagram of an electron

δm/m=0.002904,δm/m0=0.002896 。 (20)可见,不像经典电动力学点模型所认为的那样,电磁质量是电子质量的主要来源。相反地,模糊图计算表明,电磁质量只占电子质量的小部分(大约0.3%),电子质量的主要来源是其裸质量,真空电磁场的贡献很微弱。这是可以理解的,微弱的真空作用不可能导致大的贡献。

3.3 真空极化导致的电荷改变量

光子的自能图如图5所示。

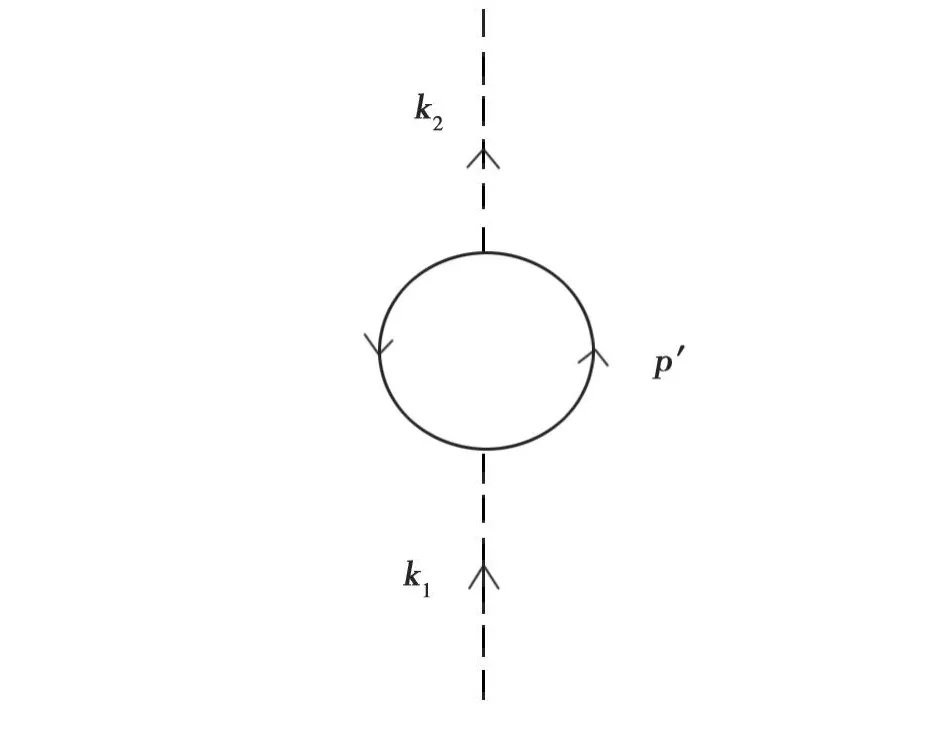
图5 光子的自能Fig.5 The self-energy graph of photon

可见,真空极化导致的电荷改变非常小,这是可以理解的,微弱的真空作用不可能导致大的电荷改变。

3.4 模糊图对于电子传播函数的一级修正

图6a反映康普顿散射的最低次近似过程之一,而图b则代表同一散射现象的较高次近似过程之一(其中的光子内线代表真空场,其隶属函数值μ<1),它的内电子线包含着电子自能。图c表示考虑质量重整化效应时的贡献[13]。因为此时考虑了质量重整化效应,故上式中的电子的质量应是实验观测质量 m0≈m。

图6 康普顿散射过程的费曼图Fig.6 Feynman graphs for Compton scattering

真空电磁场引致的电子传播子的修正应是:

式(36)和(37)中不再出现无穷大,对S矩阵元贡献的是微小的车辆射修正。

质量重整化后(考虑到绝热近似[14],这是必须的),贡献的已是微小的修正,因此就不必进一步作重整化,即利用模糊图作计算,只需进行一次质量重整化,其他的重整化诸如电荷重整化等都不需要。通常的电荷重整化程序在运算中并不是合理的,这也是有观点不赞成电荷重整化程序机制的原因之所在。更主要的是,只进行一次质量重整化有如下好处:既能修正绝热近似带来的误差,又可避免红外发散的出现(通常的红外发散就是进行电荷重整化时造成的[13]);只需质量重整化,对于不可重整化的场论如介子-核子作用、量子引力[15,16]等极为有利,不再需要引入无穷多个抵消项[17]。

4 讨论

文章对于参数Λ值的确定不是太准确(参考值),这主要由以下两点原因造成:1)F1是低级近似,不和实验结果严格相等;F1应该与重整化理论得到的同级近似结果接近,计算表明,这就要求Λ尽可能得大,但又不是无穷大。2)顶角修正中反常磁矩对Λ值的改变不敏感。后续文章中可看到,当考虑到宇宙学常数的上限限制时,Λ应该不大于Λ=2.954×1020m0,此时隶属函数μ(k)也能很好地适用于任何其他真空场的计算。尽管Λ值不太准确,但这影响不了上述结论:微弱的真空作用不可能导致大的电子质量和电荷的改变,也不可能导致大的辐射修正。

模糊图运用于场论,不仅最后结果不发散,就是计算过程中也不出现无穷大,而且还能具体解决传统理论所不能处理的电磁质量、电荷的改变量的计算问题。

就像费曼图能够由传统场论定量推导出一样,模糊图也应该有其理论基础:一种模糊场论形式(模糊理论和场论相结合的体系)。模糊场论是存在的,有意义的真空涨落、涉及到宇宙学常数问题的真空自能等等的有效计算以及Einstein引力的有意义的量子化问题,都将在这种模糊场论形式体系中作具体探讨,限于篇幅,留待另文阐述。

[1]T D Lee.粒子物理和场论简引[M].汤拒非,庆承瑞,朱重远.北京:科学出版社,1984.

[2]J D比约肯,S D德雷尔.相对论量子场[M].汪克林,郑希特,章正刚.北京:科学出版社,1984.

[3]Jean-Paul Blaizot,Andreas Ipp.Ramón Méndez-Galain,Nicolás Wschebor,Perturbation theory and non-perturbative renormalization flow in scalar field theory at finite temperature[J].Nuclear Physics A,2007,784:376-406.

[4]Christian Brouder,William Schmitt.Renormalization as a functor on bialgebras[J].Journal of Pure and Applied Algebra,2007,209:477-495.

[5]Ulrich Schollwöck.Progress in density matrix renormalization:What quantum information is teaching us.Journal of Magnetism and Magnetic Materials[M].In Press,Corrected Proof,Available online,2006.

[6]A Shindler,M Guagnelli,K Jansen,et al.Non-perturbative renormalization of moments of parton distribution functions[J].Nuclear Physics B-Proceedings Supplements,2004,129-130:278-280.

[7]ЛД朗道,ЕМ栗弗席茨.理论物理简明教程(第2卷量子力学)[M].李复龄.北京:高等教育出版社,1990.

[8]冯德益,楼世博.模糊数学方法与应用[M].北京:地震出版社,1985.

[9]刘旺金,何家儒.模糊数学导论[M].成都:四川教育出版社,1992.

[10]L A Zadeh.Aspects of Network and System Theory[M].R E Kalman,N DeClaris,New York:Rinehart&Winston,1971.

[11]L A Zadeh.Systems Approaches and Environment Problems[M].H Gottinger.Gottingen:Vandenhoeck&Ruprecht,1974.

[12]J D Bjorken,S D Drell.Relativistic Quantum Mechanics[M].Mc Graw-Hill,1965.

[13]何宝鹏,熊钰庆.量子场论导论[M].广州:华南理工大学出版社,1990.

[14]D卢里.粒子和场[M].北京:科学出版社,1981.

[15]Bryce S DeWitt.Quantum Theory of Gravity.II.The Menifestly CovariantTheory[J].Physical Review,1967,162:1195-1239.

[16]陈中秋,邵常贵.高导数量子引力的发散分析[J].湖北大学学报(自然科学版),1995,17:235-241.

[17]戴元本.相互作用的规范理论[M].北京:科学出版社,2005.

Fuzzy Graphs Describing Microcosmic Fast-speed Process