混沌宽间隔跳频序列构造法的比较
2010-10-27贺知明
胡 雁, 贺知明
(电子科技大学电子工程学院,四川 成都 611731)
0 引言
跳频通信是实现扩频通信的一种方式,无论在军事领域还是在民用通信领域它都有着广泛的发展前景。跳频系统的载波频率跳变是由伪随机序列控制的,跳频序列的性能直接影响到整个系统的性能,所以跳频序列的产生成为跳频系统设计的关键之一。跳频序列的设计应满足以下要求[1]:
①跳频序列集合中的任意两个跳频序列互相关性越小越好;
②跳频序列集合中的任意跳频序列自相关旁瓣越小越好;
③要求跳频序列集合中的序列数目尽可能多;
④各频隙在一个序列周期中的出现次数基本相同,即均匀性要好;
⑤具有好的非线性,使伪码序列具有不可逆推性,以增强抗破译性;
⑥每一个跳频序列均可以使用频隙集合中的所有频隙。
由于基于 m序列构造的跳频序列数量有限而且产生码序列的特征多项式容易获得、保密性差,随着通信技术的快速发展越来越不能满足通信的要求。而混沌信号具有频谱宽、类噪声、保密性好、易于产生、数量众多的特点,只要一个映射公式和初始值就可以产生混沌序列,它已成为目前保密通信研究的热点[2]。对于跳速已经确定的系统来说,跳频序列设计成宽间隔可更好地对抗窄带干扰、抗跟踪干扰和抗宽带阻塞式干扰以及抗多径衰落。因此对混沌宽间隔跳频序列的构造法的研究是非常有必要的。采取基于切比雪夫映射法产生混沌序列,然后用对偶频带法和圆环频带法进行宽间隔处理以得到混沌宽间隔跳频序列。
1 宽间隔跳频序列的实现
1.1 切比雪夫混沌序列
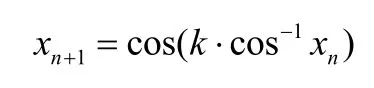
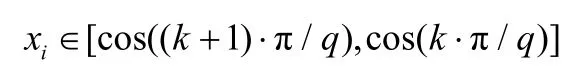
1.2 宽间隔处理
1.2.1 对偶频带法
设跳频频段为F,且要求跳频间隔不小于d,则对偶频带法的具体构造步骤如下[4]:
①将跳频频段分为两个对偶的区间频带 F1和 F2,分别为:
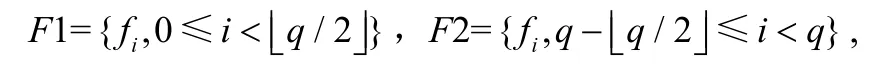
式中,q为频段F中的频率数,在F1和F2上建立对偶的频率对;
③通过一种组合方法,即当在 F1上遇到不满足宽间隔跳频要求的频率时就改跳到F2对应频率上,然后在F2上依次跳频。一旦遇到不满足宽间隔要求的频率时,又跳回到F1中对应频率上……。这样就得到一个完整的跳频序列。考虑到跳频序列首尾相接的特点,最后一个频率点与第一个频率点也应当满足宽间隔要求。如果不满足的话,将区间跳频序列中某已满足宽间隔要求的频率点再进行宽间隔处理,改跳到对偶的子频带上。
1.2.2 圆环频带法
首先将M段频段首尾相接,并且第l段首与第M段尾相连,构成具有q个点的频点环。对于圆环上任一频点,判断本次跳频点与上一个跳频点是否满足宽间隔条件。若满足则使用该频点,否则在本次跳频点的基础上再加上一个阶跃频率使得到的跳频点满足宽间隔条件,以后生成的频点也都需要加上这个阶跃频率再进行宽间隔判断[5]。这样得到的宽间隔跳频序列就完全继承了原始跳频序列的伪随机特性。
2 宽间隔跳频序列性能分析
2.1 平均跳频间隔
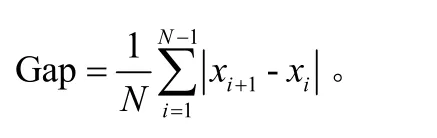
实验中切比雪夫映射中的阶数k取4,跳频频隙数q取50,跳频间隔d取10。对不同的初值和序列长度进行运算平均间隔,如表1和表2所示。
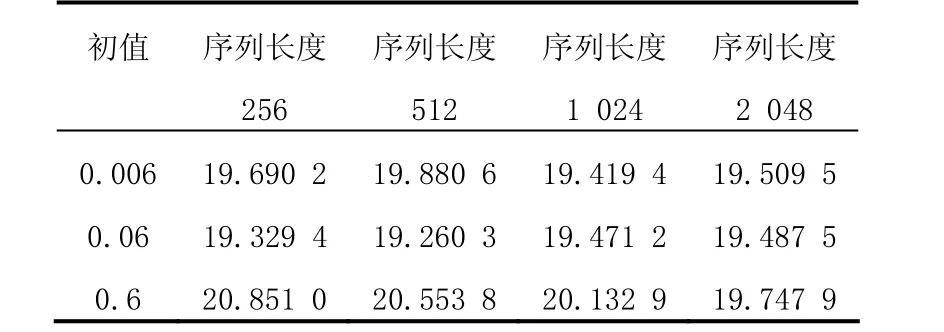
表1 圆环频带法宽间隔跳频序列的平均跳频间隔
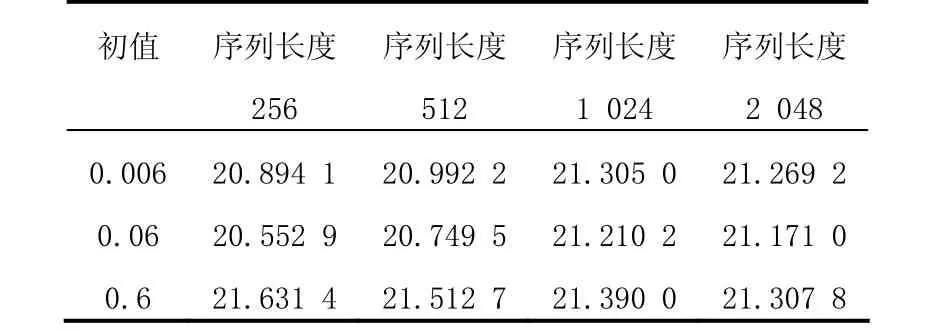
表2 对偶频带法宽间隔跳频序列的平均跳频间隔
通过表1和表2可知,对同一跳频序列采用对偶频带法处理后的平均跳频间隔稍大于采用圆环频带法的跳频序列的间隔,但两者相差不大。对不同的跳频序列分别采用这两种方法进行宽间隔处理,其平均跳频间隔有可能相同。所以这两种方法对跳频序列的平均间隔的影响相近,且两者的跳频序列长度对平均跳频间隔的影响不大。
2.2 相关性
汉明相关是衡量跳频序列族的主要指标之一。汉明自相关性能表明跳频通信的抗多径干扰的能力。在信道数一定的情况下,为增强抗多径性能,要求跳频序列的汉明自相关的主瓣尽可能地大旁瓣尽可能地小。汉明互相关性能表明跳频通信的抗多用户干扰的能力。在跳频通信中由于各个用户跳频的起始相位和传输的时延是随机的,在某一时隙可能有两个或更多个用户的信号载频跳到同一信道中,造成频隙干扰使接收机的解调输出发生误码,因此要求跳频序列的汉明互相关尽可能地小。下面就分别对宽间隔跳频序列的汉明自相关和互相关进行分析。
2.2.1 汉明自相关
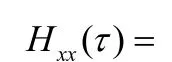
在实验中,切比雪夫映射的阶数k为4,初始值为0.35,跳频频隙数q为50,跳频间隔d为10,序列长度L分别为256、512、768、1024、1280、1536、1792和2048。经过两种方法处理后的宽间隔跳频序列的汉明自相关曲线如图1所示,横坐标为序列长度,纵坐标为自相关的最大旁瓣与主瓣的比值。从图1中可以看出,采用对偶频带法处理后的跳频序列的自相关性能明显要比采用圆环频带法好。经过这两种方法处理后的跳频序列的自相关性能都随序列长度的增长而更好。所以对偶频带构造宽间隔跳频序列的抗多径能力更强。
2.2.2 汉明互相关
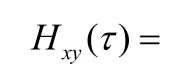
实验中任意选取两个跳频序列,设初始值为0.35和0.45。这两个序列经过宽间隔处理后的互相关性能曲线如图2所示,横坐标为序列长度,纵坐标为互相关的归一化峰值。从图2中可以看出,经过对偶频带法和圆环频带法处理后的跳频序列的互相关性能相近,但当序列长度超过1000后,经过圆环频带法处理后序列的互相关性能略好于采用对偶频带法处理的序列。两种跳频序列都随序列长度增长其互相关性能越好。
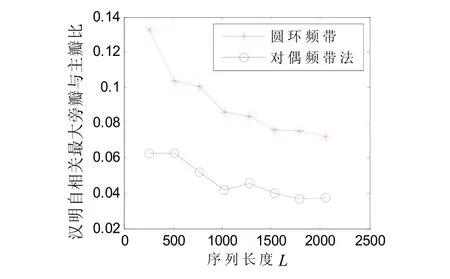
图1 不同宽间隔处理的跳频序列的自相关性能
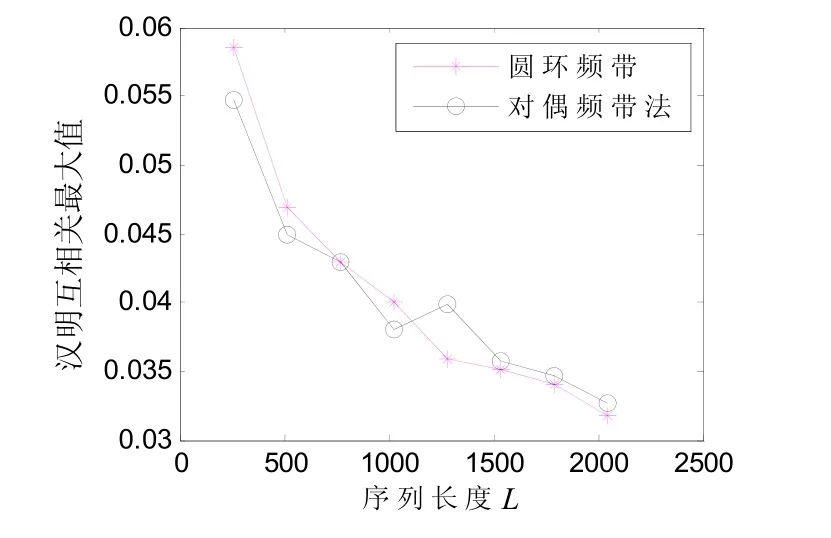
图2 不同宽间隔处的跳频序列的互相关性能
2.3 平衡性
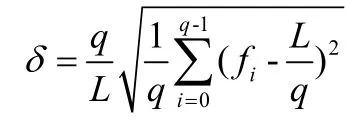
实验中切比雪夫映射的阶数k为4,初始值为0.35,跳频频隙数q为50,跳频间隔d为10,序列长度L分别为256、512、768、1024、1280、1536、1792、2048。经过两种方法处理后的跳频序列的平衡特性曲线如图3所示,横坐标为序列长度,纵坐标为平衡性参数。从图3中可以看出,两者的平衡性相近。当序列长度超过800时,采用对偶频带法的跳频序列的平衡性略好于圆环频带法的跳频序列。两者序列长度越长其平衡性越好。
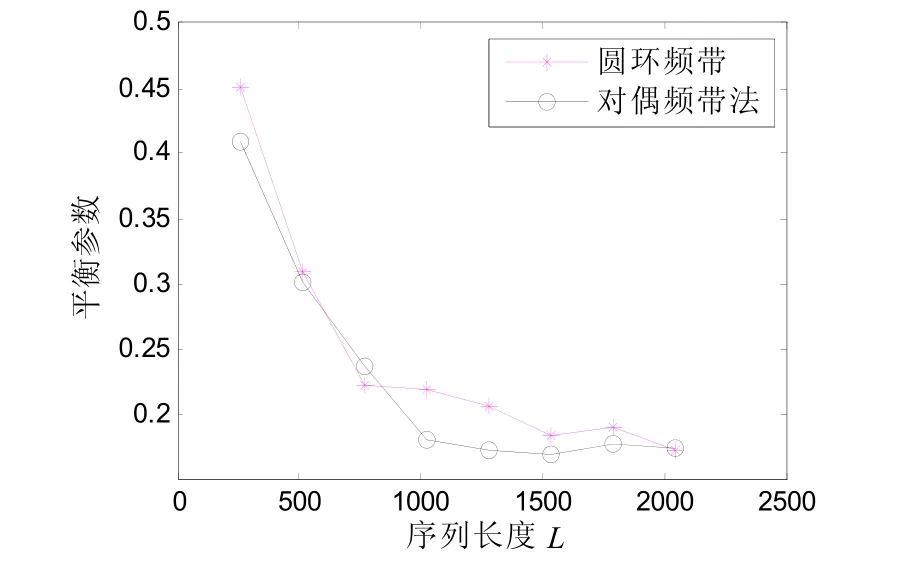
图3 不同宽间隔处理的跳频序列的平衡性
3 结语
通过上述分析可知,对偶频带法和圆环频带法均能实现宽间隔跳频序列。对偶频带法能带来很好的自相关性,使系统具有更强的抗多径衰落性,但适用于偶数个频隙的跳频系统。圆环频带法在跳频序列长度较长时具有良好的互相关性,且能均匀使用全部频隙而不受频隙个数的奇偶性的影响。
[1]和丽芳.混沌跳频序列的产生及其在跳频通信系统中的应用[D].昆明:昆明理工大学,2005.
[2]黄乘顺,李星亮.基于混沌的扩频通信系统及性能分析[J].通信技术,2008,41(12):37-39.
[3]孙克辉,周家令,牟俊.多用户混沌序列扩频通信系统设计与性能分析[J].电子与信息学报,2007,29(10):2436-2440.
[4]梅文华,张志刚.一类新的宽间隔跳频序列族的构造[J].电波科学学报,2002,17(01):16-20.
[5]胡建凯,曾兴雯.扩频通信系统中跳频图案的设计实现[J].无线通信技术,2002(02):34-37.
[6]牛犇,李文臣.一种新的混沌宽间隔跳频序列的构造方法及其Matlab仿真分析[J].南开大学学报:自然科学版,2005,38(03):49-52.
[7]HELLESETH T, KUMAR P V, MARTINSEN H.A New Family of Ternary Sequences with Ideal Two Level Autocorrelation Function[J].Designs, codes and cryptography, 2001(23):157-166.
[8]陈宇,王文海.基于混合映射产生跳频序列的新方法[J].通信技术,2008,41(12):75-77.
