超宽带通信系统中同步算法研究
2010-09-25杜鹃,刘伟
杜 鹃, 刘 伟
(①重庆通信学院,重庆 400035;②中国人民解放军通信指挥学院,湖北 武汉 430010)
0 引言
自上世纪 90年代初以来,无线通信技术得到了迅猛发展,人们对无线业务的需求也在持续增长,各种满足不同需求的无线通信系统也应运而生。UWB技术具有传输速率高、系统容量大、成本低等特点,因此成为解决热点地区高速无线接入需求与紧张的频谱资源之间矛盾的有效方案[1-2]。
在超宽带通信系统中,由于UWB信号持续时间非常短,因此同步问题成为影响系统性能的关键问题。接收端只有清楚地知道接收信号的传输时延、将本地脉冲信号与其同步,才能实现对期望信号的完成相干或者非相干接收[3]。由于UWB系统采用纳秒级的脉冲作为信息的载体,即使较小的同步误差也可能会造成相当大的性能下降。此外,UWB信号在传播过程中多径分量丰富,在某些复杂环境中多径时延较大[4],而且UWB信号功率谱密度很低,这使得UWB无线通信系统中的同步的要求增高。
目前受到较多关注的同步方法是利用接收信号自身进行相关的脏模板同步方法[5-6],该方法不需要训练导频,算法复杂度较低。采用相干方式的同步算法能获得较好的性能,但是往往复杂度相对要高。为平衡这两种同步算法的性能和复杂度,提出一种UWB系统中的粗细同步相结合的同步方法,分别是粗同步(捕获)和细同步(跟踪)。采用脏模板同步算法完成捕获,然后在捕获的基础上采用滑动相关完成细同步过程,针对TH-UWB-PAM系统给出了算法设计,并通过仿真实验验证了该同步算法的有效性。
1 TH-UWB-PAM系统信号模型
以跳时超宽带系统中脉冲幅度调制的TH-UWB-PAM信号为例,发射信号可表示为:
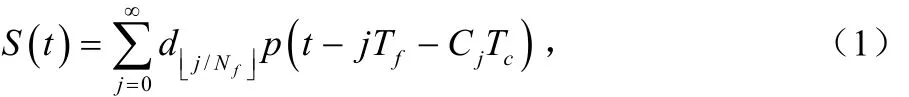
式中, dj∈ {- 1 ,1},”表示向下取整运算,每 Nf个脉冲波形传送一个二进制比特; Tf为脉冲重复周期; Cj为为伪随机跳时序列的第 j个码元(0< Cj<Nmax),Tc是码片时间。
设跳时码的周期为 Tp,且 Tp= Tf,并把一个数据码元的持续时间记为 Tb,故 Tb= NfTf。因此上式可以写为:
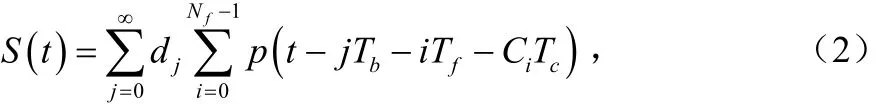

UWB多径信道采用抽头延迟线模型,设抽头数目为L,其路径增益和延时分别为假定信道为准静态,即信道参数和延时不发生变化,为了将多径与传输时延0τ相区别,所有路径延时可以唯一表示为τl.0=τl-τ0,则多径信道模型为:UWB信号经过多径信道传播后,接收信号为:
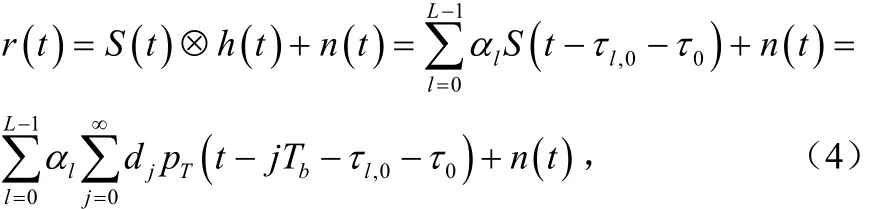
式中, n(t)是零均值的高斯白噪声。令接收码元的信号表示为:,则接收信号可以写为:
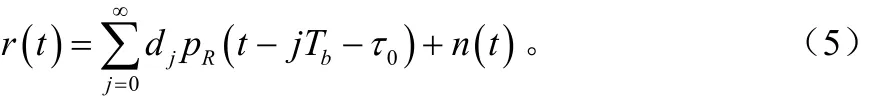
2 TH-UWB-PAM系统的同步捕获算法
2.1 粗同步(捕获)算法
该同步算法中首先采用脏模板算法来实现粗同步即捕获过程,具体做法是利用相邻两个码元长的、受多径信道和噪声影响的接收信号互为模板,做互相关运算来实现帧一级的同步。其算法原理分析如下:
从接收信号中取一个符号长度 Tb的信号波形,起始时刻为 t0+ n Tf+ m Tb,其中 t0∈;n,m为整数,为观察窗的长度。信号表示如下:
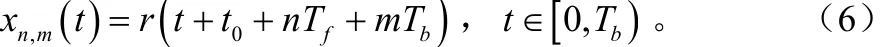
为了利用相邻两个符号长的接收信号之间做互相关运算得到的信息获得同步,对相邻两个符号长的信号做互相关:
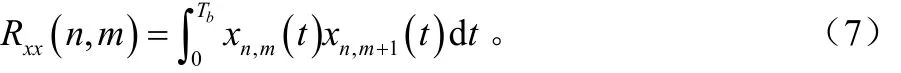
对所得到的相关值取绝对值,由于 Rxx(n, m ) 的值只与n有 关[17], 所 以 Rxx(n, m ) 可 以 写 成 Rxx(n ) 。 令则粗同步所捕获的时延值τ= t0+ nεTf。
实际中使用求时间平均的方式求数学期望,即在观察窗长 M Tb的范围内求 Rxx(n ) ,有:
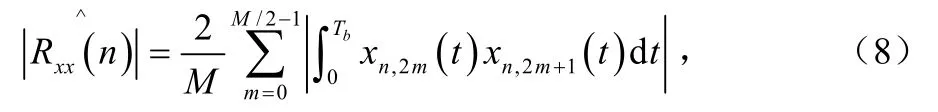
这样在经过粗同步算法后,所捕获的时延值为:
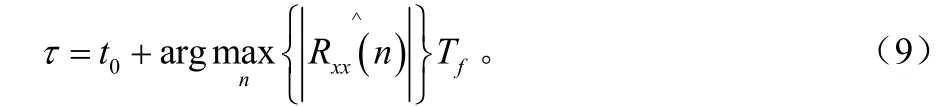
粗同步(捕获)算法过程可归纳为如下步骤:
①从时刻n=0开始,把接收到的信号按每段一个符号长Tb分成M段,将其中第m段信号 xn,m(t)和与其相邻的第m+ 1段信号 xn,m+1(t ) 做式(7)所示的运算;
②对步骤②中得到的 M / 2个相关值得绝对值求和后再求平均,如式(8)所示。此时,若 n <Nf-1,则令n=n+1,并继续步骤②的运算;否则,进行步骤④的运算。这样共可得到 Nf个 Rxx(n ) 的估计值;
③由步骤③可以得出 Rxx(n)的 Nf个值,取其中最大值所对应的n,并记为则可以认为τ= t0+ nεTf就是所要捕获的时延值。
2.2 细同步(跟踪)算法
在上述讨论的捕获算法基础上,再利用理想的本地脉冲信号与接收信号在两帧的长度范围内做滑动相关,来提高同步精度,最终实现细同步(跟踪)。具体算法流程可分为:
①接收信号与理想的本地信号,分别做式(10)和式(11)所示的相关运算。其中 r(t)为接收信号, s(t)为一个码元长度的本地信号, Tb为码元长度,n从0取到 Tf, t ∈[0 ,Tb],ε∈ [τ - n ,τ],相关运算表示为:
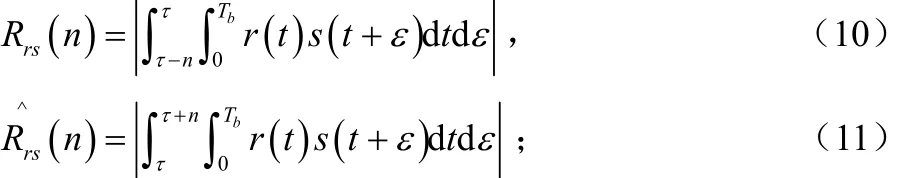
3 同步算法性能仿真与分析
3.1 实验参数设置和性能评价标准
在仿真实验中,采用高斯脉冲二阶微分形式作为接收到的脉冲,脉冲宽度 Tp=0.5 ns,每个符号用 Nf帧表示,帧周期 Tf=10 ns,每个符号的长度 Tb= NfTf。在做同步捕获的性能仿真时,同步捕获的性能是通过同步的均方误差对 Tb2进行归一化来衡量的。通过仿真可以得到归一化均方误差关于信噪比的性能曲线,这里,信噪比定义为每个脉冲接收能量ERX(注意,这里的 ERX是每脉冲的总接收能量,即接收机获得的一个发射脉冲经多径信道传播后的所有多径分量之和)与单边噪声功率谱密度 N0之比。观察窗长度为 M Ts。
实验中设首径时延为τ0,第i次同步捕获后得到的同步位置为τi,由此得到的归一化同步捕获均方误差为:

3.2 粗同步实验及性能分析
仿真实验首先分别给出M取4、8、16、32、64时,粗同步算法在AWGN信道下的粗同步归一化均方误差(MSE)性能曲线,如图1所示。同样在多径信道下,得出粗同步归一化均方误差性能曲线,如图2所示,其中对曲线的说明可参照图1。从两种信道下的归一化均方误差性能曲线可以看出:在帧数Nf和每个符号长度 Tb一定的情况下,粗同步(捕获)算法的归一化均方误差与所取的观察窗长度 M Tb有关,即与M有关,M 越大,误差越小,即同步精度越高。由于每次步进是 Tf,当信噪比增加到一定的时候,归一化均方误差曲线末端平坦,另外在多径信道下能获得与AWGN信道近似的性能。
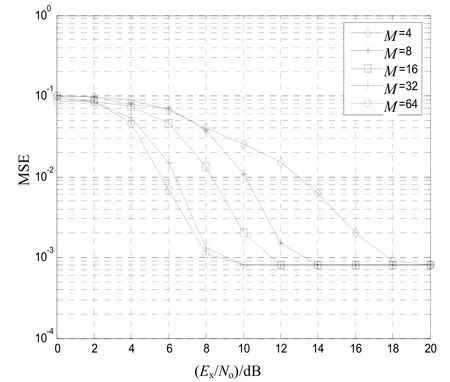
图1 AWGN信道下的粗同步误差曲线
3.3 细同步实验及性能分析
现进一步考察在粗同步基础上进行滑动相关实现细同步的性能。为简单起见,仅选取了当M=8(图中星号所示)和M=64(图中圆圈所示)的情况。在AWGN信道下,得到的细同步(跟踪)归一化均方误差性能曲线如图3所示。在多径信道下得到的细同步归一化均方误差性能曲线如图4所示。从两图中可以看出,在信噪比较低时,粗同步精度达不到0.01,在此基础上做滑动相关对同步性能改善不明显;在信噪比较高时,粗同步精度能够满足要求,做滑动相关就可以很好地实现细同步。图3中,当信噪比大于4 dB时,细同步过程已经完全同步;图4中,当信噪比大于6 dB时,细同步已经完全同步。
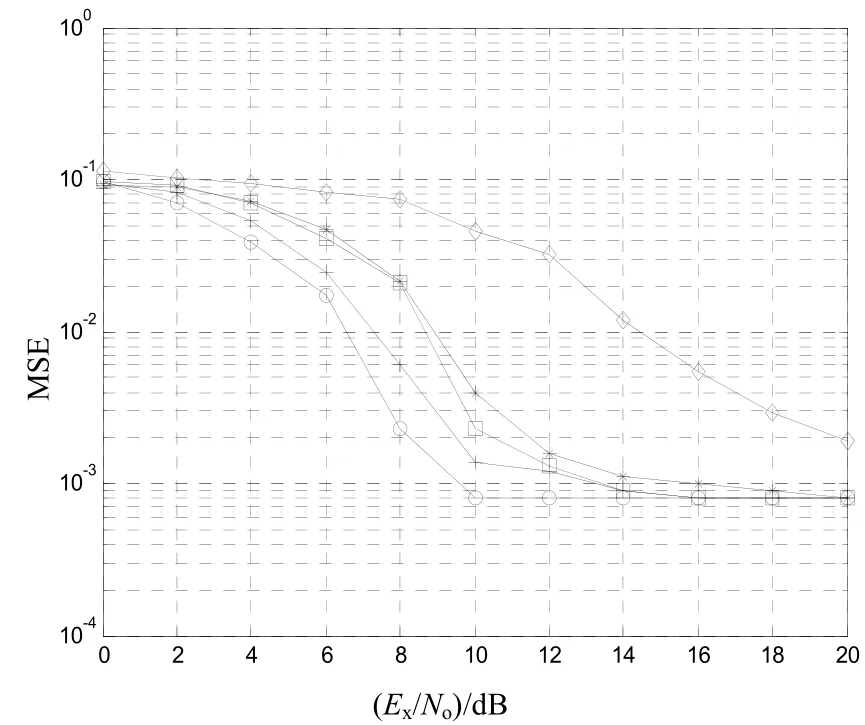
图2 多径信道下的粗同步误差曲线
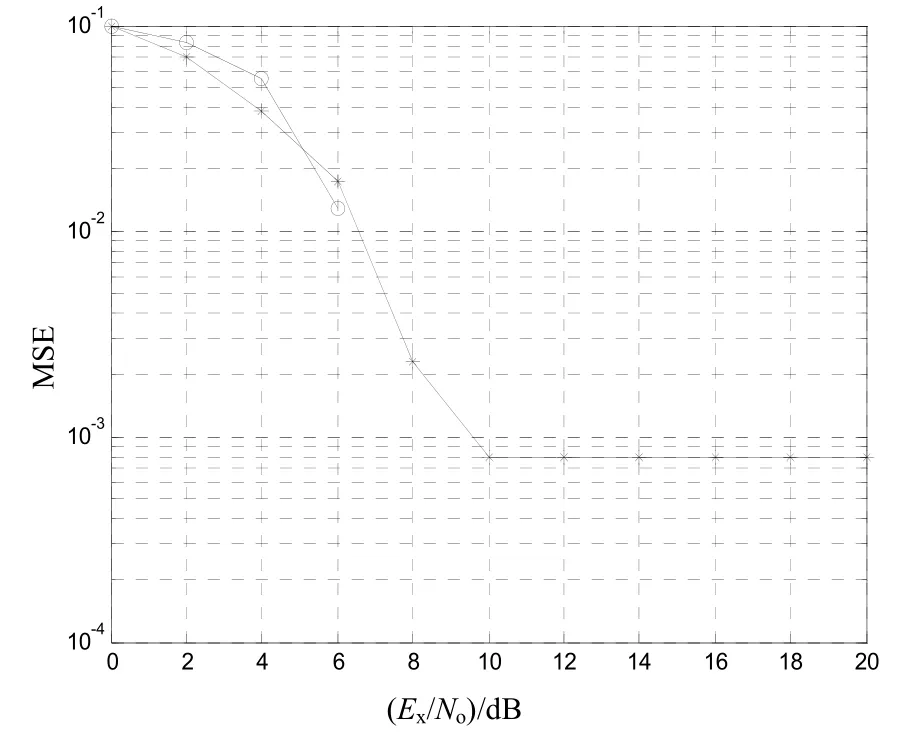
图4 多径信道下细同步误差曲线
4 结语
给出一种粗细同步相结合的超宽带通信系统中的同步方法,首先采用脏模板算法完成粗同步,即接收信号的捕获过程;随后在捕获的基础上利用滑动相关算法进行细同步,即跟踪。通过仿真实验在AWGN和多径信道下验证了该同步算法的有效性,同时也发现算法同步性能需要一定的粗同步精度,才能利用后续的细同步来提高系统的同步精度。后续研究中继续探讨超宽带通信系统中多址干扰等存在时的同步定时算法。
[1] YANG L Q, GIANNAKIS G B. Ultra-wideband Communications an Idea Whose Time Has Come[J]. IEEE Signal Processing Mag, 2005(11):26-54.
[2] 蔡雨.一种密集多径环境下 UWB信号到达角的估计方法[J].通信技术,2009, 42(08): 161-164.
[3] 胡琳,王洪玉.基于最大似然准则的超宽带分簇信道估计[J].通信技术,2009,42(08): 37-39.
[4] MOLISCH A F, BALAKRISHNAN K, CHONG C C. IEEE 802.15.4a Channel Model-final Report [EB/OL] (2005-03-12) [2009-12-01].http://www.ieee802.org/15/pub/TG4a.html.
[5] YANG L Q, GIANNAKIS G B. Timing Ultra-wideband Signals with Dirty Templates[J]. IEEE Trans. on Wireless Communications,2005, 53 (04): 1952-1963.
[6] Xu H, Yang L. Timing with Dirty Templates for Low-Resolution Digital UWB Receivers[J]. IEEE Transactions on Wireless Communications. 2008, 7(01): 54-59.
