聚合物结晶过程及动力学模型

王锦燕,孙玉周,李冬霞

(中原工学院,郑州 450007)

聚合物结晶过程及动力学模型

王锦燕,孙玉周,李冬霞

(中原工学院,郑州 450007)

介绍了结晶聚合物在静态和流动诱导下的结晶动力学模型和研究进展,并进行了比较和讨论,指出目前的模型模拟结果与成型加工中真实的结晶过程仍有差距.

聚合物;结晶;动力学;模型

在聚合物材料中,具有结晶能力者占有相当的比例,但和低分子材料不同的是,其结晶往往不完善、只能部分结晶、结晶过程也较复杂.聚合物的结晶结构和结晶行为对材料的性能,如尺寸精度、尺寸稳定性、热传导系数、模量和强度产生重大影响,进而决定成型制品的最终用途[1].静态条件下聚合物的结晶行为研究已经比较完善,但在实际的成型过程,如挤出、注射、吹膜及纺丝等过程中,聚合物经历不同的外力作用和温度场变化,在这些外力的作用下聚合物的结晶行为有了很大改变[2-4],通常剪切缩短了聚合物的成核诱导时间,并大大增加成核密度,缩短结晶时间.同时剪切使聚合物的结晶形态发生变化,产生比静态条件下更丰富的结晶形态,如片晶、柱晶、串晶等.CA E技术已成为聚合物产品开发、模具设计及产品加工中薄弱环节的有效解决途径,但CAE技术的核心是建立可靠的数学模型,目前很多学者提出有关结晶动力学、结晶形态学及结晶流变学的数学模型,并模拟不同流场、不同温度场下的结晶行为[5-8].

聚合物结晶动力学是聚合物物理中的一个热门课题之一,研究不同条件下聚合物的宏观结晶与结构参数随时间变化规律[9-10],也就是研究不同条件下结晶度随时间的变化规律,主要关注成核速度和晶体生长速度,进而得到不同加工条件下结晶诱导时间、半结晶时间、结晶度等物性参数.

1 静态结晶动力学

1.1 静态等温结晶动力学

静态结晶动力学可分为等温和非等温结晶动力学.等温结晶是将在熔点温度以上聚合物熔体快速冷却至某结晶温度,保持此温度直至结晶完成,也可从聚合物熔体快速淬火到玻璃化温度以下形成玻璃态,然后快速升温至某一温度进行等温冷结晶.常用的测试手段有膨胀计法、热台偏光显微镜法、差示扫描量热法等.Avrami方程[11]是研究等温结晶的经典理论,描述为:

式中,左部分为t时刻未收缩体积分数;Vt-V∞为任一时刻t时未收缩的体积;V 0-V∞为结晶完全时最大的体积收缩;k为结晶速率常数;n为Avrami指数.通过实验数据可得到n和k值,获得有关结晶过程的成核机理、生长方式及结晶速度等信息.

1.2 静态非等温结晶动力学

非等温结晶是研究在变化的温度场下聚合物的结晶过程,可分为等速升、降温和变速升、降温过程.由于非等温结晶动力学过程比较复杂,目前的理论和数据处理方法较多,常见有:

(1)Ozawa法.Ozawa[10]基于Evans理论,从聚合物结晶的成核和生长出发,导出等速升温和等速降温时的结晶动力学方程:

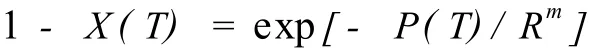
式中:X(T)为温度 T时的相对结晶度;R为升温或降温速率;m为Ozawa指数;P(T)为与成核方式、成核速率和晶核的生长速率有关的冷却函数.该方法成功地应用于聚对苯二甲酸已二酯、聚丙烯、尼龙 -6等,但该方法的不足在于在不同的冷却速率下,聚合物结晶的温度区间相差较大,处理实验结果有很大的局限性.

(2)Nakamura方法.Nakamura[12]在等动力学的基础上对Avrami等温结晶理论进行扩展,假定成核和生长2个阶段具有相同的温度依赖性,提出非等温动力学模型:

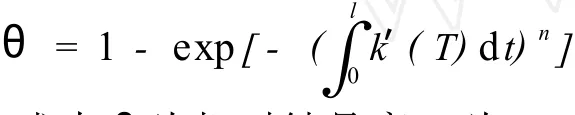
式中:θ为相对结晶度;n为Avrami指数;k′(T)为非等温结晶速率,与等温结晶速率的关系为:

式中,k(T)为等温结晶速率;t1/2为半结晶时间.

(3)Ziabicki方法.Ziabicki[13]将非等温结晶看成是忽略二次结晶条件下的多个连续的等温结晶过程,在准晶态条件下,结晶成核和生长速率由热历史控制,结晶时间受外部条件变化的影响,描述结晶过程为:

式中:α为结晶度;K(T)为结晶速率常数.

该模型忽略了所有非稳定状态的影响,这时成核和生长速率的时间依赖性只由外部条件的改变引起,或者只由热机理控制,即Avrami指数为常数.

(4)Privalko方法.Privalko[2]将Avrami方程写成如下形式:

式中:X为t时刻的结晶转化率;K＊=zt/φn为有效速率常数;降温速率与时间的乘积 φt称为比对时间,相当于单位冷却速率下的结晶时间.该方法的优点是处理方法简单,只从一条DSC升温或降温曲线就能获得Avram i指数和表征结晶速率的参数,缺点是所得到的结晶速率参数缺乏明确的物理意义.

2 剪切诱导结晶动力学

剪切通常被认为是“微弱”的流动,但发现剪切可以加速聚合物的结晶,这种加速作用关键体现在成核过程中,增加成核生长速率,缩短成核诱导时间,大大增加成核密度.诸多学者提出了很多不同的动力学模型,本文主要针对流动引起材料结晶成核速率的变化的动力学模型作简单介绍,Avrami方程[14-15]描述结晶度α的表达式为:

α=1-exp(-αf)

式中,虚拟体积数αf为:

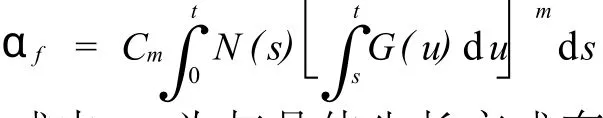
式中,m为与晶体生长方式有关的指数,取值1～3,对于球形生长 m=3,Cm=4π/3;对于棒状生长m=1,Cm表示棒的横截面;G(u)为晶体生长速度;N(s)为晶体成核速率,施加剪切后活化晶核数N为静态和流动诱导2部分晶核数之和:

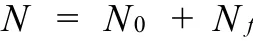
Km、Binsbergen和Angelloz指出静态成核数 N0与结晶温度 T间的关系[3]:

式中:a、b为常数;ΔT=T0m-T,T0m为平衡熔点.

通常使用经典的Lauritizen-Hoffmann方程描述不同温度 T下晶体生长速率G:

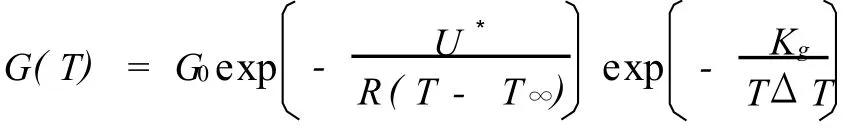
式中:G0为与温度无关的前置因子;U＊为链段穿过液固界面到达结晶表面所需的活化能;R为气体常数;Kg为与温度无关的成核指数;T∞为没有分子迁移时的温度,通常为:

Koscher和Fulchiron研究认为[3]晶体生长速度主要与温度有关,受流动的影响不大,但许多学者研究认为.由于流动诱导的成核速率 Nf却与流场和温度有很大的关系.因此,对于流动诱导结晶动力学的研究主要体现在成核速率,不同学者提出不同的成核速率表达式,得出不同的结晶动力学模型.根据促进成核速率增长的机理,目前常用模型有:

(1)剪切速率.Eder等通过实验提出与剪切速率相关的模型,把剪切速率作为结晶的驱动力,认为在流动诱导结晶中能够发生成核的点都是由流动产生的:

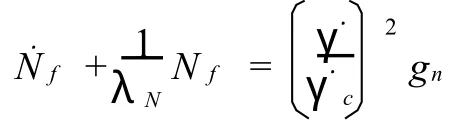
式中:λN为松弛时间;.γc为临界活化剪切速率;gn为与成核数目有关的常数.

(2)应变.将流动诱导成核速率表示成应变γ(γ=.γt)的函数:.Nf=A(.γt)r,其中A、r为常数.

(3)法向应力差.在流变学中,第一法向 N1反应了流变行为中的弹性部分,使分子发生取向,部分倾向于形成晶核,Zuidema等通过实验提出流动诱导活化晶核数目与第一法向应力差的关系:

Emmanuelle Koscher[3]根据该模型模拟了流动诱导结晶过程,研究了剪切时间、温度、剪切速率和剪切应变对活化晶核数目、相对结晶度、半结晶时间的影响,与实验有定性一致的结果.作者认为该模型通过第一法向应力差考虑了聚合物熔体的流变行为,有一定的优越性,并指出该模型可定性分析剪切对不同分子量分布聚丙烯结晶行为的影响.

(4)可恢复应变.认为促进成核速率增长的诱因不是流动本身,而是经历流动作用的聚合物,将成核速率表达成可恢复应变(弹性Finger张量)的函数:

式中:λN为松弛时间;参数gn′表征J2对成核数目的影响;J2为可恢复应变Be偏导部分的第二不变量:

Gerrit W M Peters[7]根据该模型模拟了剪切和拉伸流场下晶核数目随剪切时间的变化及制品的结晶度,认为材料本身经历的变化而非外因是成核速率增长的动力,指出该模型优于Eder的剪切速率模型.

(5)活化能.通过流动引起聚合物自由能的变化,研究流动对成核速率的影响:

其中,λN为松弛时间;f是有关流动的函数:

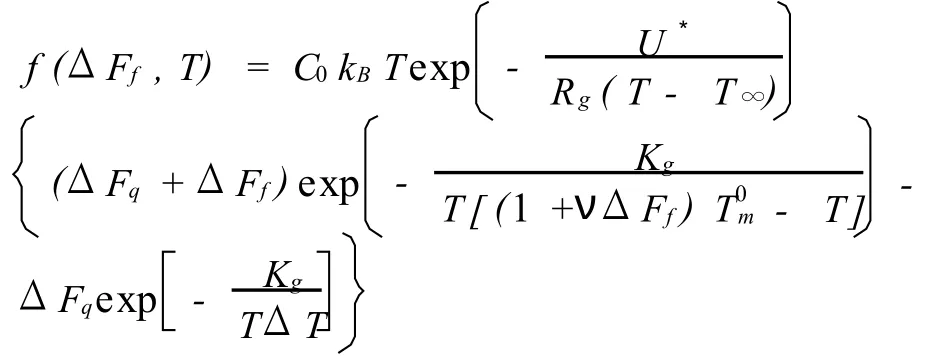
式中:C0为包含能量和尺寸的常数;kB是Boltzmann常数;为平衡熔点,通常只与压力有关;ΔFq为静态Gibbs自由能,通常为ΔFq=ΔH0ΔT/T0m,参数 v=/(ΔH0T),ΔH0为结晶潜热;ΔFf为流动引起的自由能变化.

Zheng R[8]根据该模型模拟了不同剪切时间、剪切速率和剪切应变对结晶度、晶核数、半结晶时间的影响,取得较好结果.

3 结 语

Emmanuelle Koscher[3]根据流动诱导晶核数目与法向应力差的关系模型模拟了流动诱导结晶过程,研究了剪切时间、温度、剪切速率和剪切应变对活化晶核数目、相对结晶度、半结晶时间的影响,与实验有定性一致的结果,并指出该模型可定性分析剪切对不同分子量分布聚丙烯结晶行为的影响。Zheng R[8]根据该晶核数目与活化能的关系模型模拟了不同剪切时间、剪切速率和剪切应变对结晶度、晶核数、半结晶时间的影响,取得了较好结果。Gerrit W M Peters[7]根据可恢复应变模型模拟了剪切和拉伸流畅下晶核数目随剪切时间的变化,及制品的结晶度,认为材料本身经历的变化而非外因是成核速率增长的动力,指出该模型优于 Eder的剪切速率模型。申长雨等[5-6]从结晶动力学和结晶热力学出发,结合材料在注射充填过程中的流体动力学基本方程,考虑结晶对加工过程温度场的影响,对聚合物的结晶行为进行模拟分析。由于实验手段的局限性,目前学者的研究多是定性分析结晶对聚合物成型的影响,仍与实际加工中复杂的热力场和流场有一定差距,需要科研工作者的深入研究,逐步完善材料结晶理论和模型,使模拟实际加工成为可能。

[1] 陈青,范毓润,郑强.剪切流场诱导ipp等温结晶行为的研究[J].高分子学报,2007(5):467-470.

[2] Privalko V P,Kawai T,Lipatov Y S.Crystallization of Filled Nylon 6[J].Non-isothermal Crystallization Colloid Polym Sci.,1979,257:1044-1048.

[3] Emmanuelle Koscher,Rene Fulchiron.Influence of Shear on Polyp ropylene Crystallization:Morphology Development and Kinetics[J].Polymer,2002,43:6931-6942.

[4] 杨伟.半晶聚合物的应力应变行为及其与形态结构的关系[D].成都:四川大学,2006.

[5] 沈俊芳,陈静波,周应国,等.聚合物结晶过程及计算机模拟研究进展[J].高分子材料科学与工程,2007,23(1):1-5.

[6] 申长雨,周应国,陈静波.半结晶聚合物注射成型中结晶动力学的数值模拟[J].高分子学报,2008(8):771-777.

[7] Gerrit W M Peters,Frank Swartjes H M,Han Meijer E H.A Recoverable Strain-Based Model for Flow-Induced Crystallization[J].Macromol.Symp.,2002,185:277-292.

[8] Zheng R,Kennedy P K.A model for Post-Flow Induced Crystallization:General Equations and Predictions[J].J.Rheol.,2004,48(4):823-842.

[9] 张志英.聚合物结晶动力学理论和方法研究[D].天津:天津工业大学,2006.

[10] Ozawa T.Kineticsof Non-isothermal Crystallization[J].Polymer,1971,12:150-154.

[11] Avrami M.Kinetics of Phase Change,IGeneral Theory[J].J.Chen Phys.,1939,7(12):1103-1110.

[12] Nakamura K,Katayama K,Amano T.Some Aspects of Nonisothermal Crystallization of Polymers[J].J App l Polym Sci.,1973,17:1031-1035.

[13] Ziabicki A.Development of Structure in Processing Polymers Composed of Flexible Vs,Rigid Molecules[J].Polym Adv Tech.,1987(6):580-601.

[14] Roger Tanner I,Fuzhong Qi J.A Comparison of Some Models fo r Describing Polymer Crystallization at Low Deformation Rates[J].Non-new tonian Fluid Mech.,2005,127:131-141.

[15] Salvato re Coppola,Nino Grizzuti.M icro rheological Modeling of Flow-Induced Crystallization[J].Macromolecules,2001,34:5030-5036.

Development and Dynam ic Models for Polymer Crystallization

WANG Jin-yan,SUN Yu-zhou,L IDong-xia
(Zhongyuan University of Technology,Zhengzhou 450007,China)

A num ber of mathematical models fo r polymer crystallization development under quiescent and shearing conditions are introduced.Compared w ith the performance of various dynamic models,it points out that the p resent models can not show the true crystallization p rocess.

polymer;crystallization;dynam ic;model

O631

A DO I:10.3969/j.issn.1671-6906.2010.01.017

1671-6906(2010)01-0066-03

2009-12-15

王锦燕(1973-),女,河南洛阳人,讲师,硕士.