可拓灰局势决策在织物舒适性评价中的应用

王永林,王东云,宋百平

(中原工学院,郑州 450007)

可拓灰局势决策在织物舒适性评价中的应用

王永林,王东云,宋百平

(中原工学院,郑州 450007)

将可拓学和灰色理论相结合的可拓灰局势决策引入到织物性能评价中,建立了局势、对策、效果测度和权重的物元描述形式,给出了决策过程.选用吸湿性、芯吸高度、透湿性、快干性、透气性和保暖性等6项指标对12个织物样本的热湿舒适性能进行了可拓灰局势决策,给出了计算过程和结果,为选择服装面料提供了一种参考依据.

可拓学;物元;灰局势决策;织物性能

服装的舒适性由织物的保暖性、透气性、吸湿性、透湿性等因素决定.为了能优选出合适的服装面料,必须对织物的性能进行评价,人们在这方面做了大量研究,提出了一些方法,如人体着装实验法、暖体假人法、模糊评判法等[1-3].织物的性能在测量前,很多信息是不明确的,具有灰色性;进行有关测定后,不同织物各指标数据各有优劣,采用单一指标评价的结果往往具有矛盾性,并且有的指标对总体性能起积极作用,有的起消极作用.本文采用处理信息不完全问题的灰系统理论与解决矛盾和不相容问题的可拓学相结合的可拓灰局势决策方法对织物的热湿舒适性进行评价,给出了有关步骤和评价例子.

1 可拓灰局势决策

1.1 构建局势物元和对策物元

局势由事件和对策构成[4].用物元描述局势更加直观.物元由事物、特征和量值3个要素构成[5],采用物元结构,局势物元表示如下:

其中:si表示第 i个局势,i=1,2,…,m,m为局势数;a表示事件;⊗bi为si对应的对策,它有自己的特征和量值,也是一个物元,该物元中蕴含着效果测度.因对策尚未白化,该局势物元可称为灰色物元[6],简称灰元.事件可以有多个,比如“优选服装面料”是1个事件,“优选冬季服装面料”和“优选夏季服装面料”是2个事件,它们可以有相同的对策集.对策物元的特征为局势决策中的目标,如果量值确定的话,称为对策白元,即通常意义的物元,这里用bi表示;如果量值信息不明确,则称为对策灰元.n个目标_的n维对策物元可表示如下:

其中:cj为第j个指标(目标);vj为对应的量值;j=1,2,…,n,n为目标数.如果量值具有模糊性,则称该物元为模糊物元[7].

m个对策物元可以构成复合物元:

1.2 确定目标正负极性,求效果测度物元

效果测度可认为是对策中某个目标满足局势中对应目标要求的程度,一般要求具有正极性,也就是数值越大越好.如果采用隶属函数求效果测度,效果测度就是模糊隶属度;如果采用可拓关联函数求效果测度,效果测度就是可拓关联度,由于可拓关联函数值域为整个实轴,所以可拓关联度可以包含隶属度,两者在特定情况下可以等同.一种简单的求效果测度的公式为:

对于正极性指标:

1.3 建立权重物元,求统一测度物元

在多指标综合评判中,各指标对总目标的影响程度不同,用权重来衡量,如果重要程度一样,则为等权情况.权重物元表示如下:

一般采用加权求和法求统一测度.统一测度物元可表示如下:

1.4 求满意局势物元

由最大统一测度法求满意局势物元:

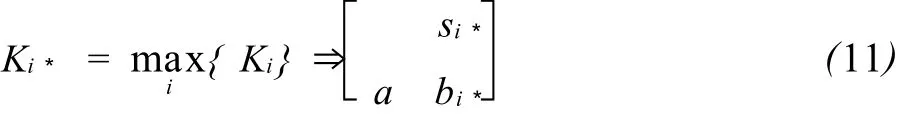
其中:si＊为满意局势;bi＊为α的满意对策.

2 应用实例

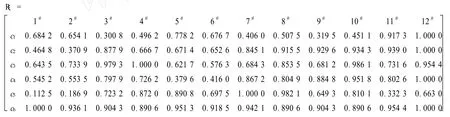
影响织物热湿舒适性的指标有多种,这里选用吸湿性、芯吸高度、透湿性、快干性、透气性和保暖率等6项指标,分别记为 c1、c2、c3、c4、c5和 c6,对不同组织规格的12种面料进行评价,热湿舒适性参数如表1所示[3].

表1 织物热湿舒适性参数

由表1可知,从数值上分析,吸湿性12#最大,3#最小;芯吸高度12#最大,2#最小;透湿性4#最大,6#最小;快干性12#最大,5#最小;透气性7#最大,1#最小;保暖率4#、8#和10#最大,1#和12#最小.可见不同织物在各指标性能上各有优劣,不能给出简单的直观判断,这里采用可拓灰局势决策进行优选排序.

2.1 构建局势物元和对策物元

对于织物舒适性评价,其事件是选择织物,目标是性能指标,对策是选用不同规格的织物,这里对策数m=12,指标数n=6.由表1数据可构建12对策6维复合物元:

2.2 确定目标正负极性,求效果测度物元

对于热湿舒适性,有些指标的正负极性在冬季与夏季不同,在夏季,保暖率越小越好,为负极性,其余指标为正极性;在冬季所有指标都按正极性处理.采用公式(4)、公式(5)处理后,可得效果测度物元矩阵.下面为优选夏季服装面料的效果测度物元矩阵.

2.3 建立权重物元,求统一测度物元

采用问卷调查法,得权重物元如下:

根据公式(9),对指标加权求和,可求得统一测度物元:

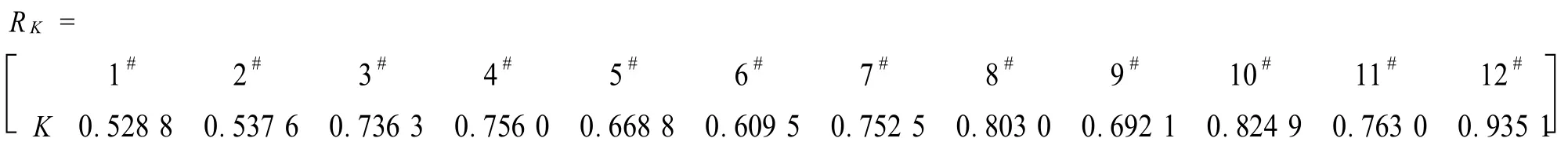
2.4 求满意局势物元

根据公式(11):

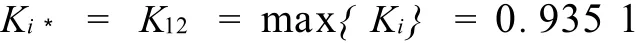
则s12为最优局势,即对夏季服装,12#织物热湿舒适性最优.各织物优劣排序为:

12#＞10#＞8#＞11#＞4#＞7#＞3#＞9#＞5#＞6#＞2#＞1#

等权情况下各织物优劣排序为:

12#＞10#＞8#＞7#＞11#＞4#＞3#＞9#＞5#＞6#＞1#＞2#

若优选冬季服装面料,采用问卷调查的权重,各织物排序为:

12#＞10#＞8#＞11#＞4#＞7#＞3#＞9#＞5#＞6#＞2#＞1#

等权情况下各织物排序为:

12#＞10#＞8#＞4#＞7#＞3#＞11#＞9#＞5#＞6#＞2#＞1#

由此可知在优选冬季服装面料时,仍然是12#织物性能最优.根据排序情况,可选出1～2个备选样本.不等权时,由于保暖率权重较小,冬季和夏季的不同要求没有影响织物的排序;等权时有影响.

3 结 语

采用可拓学与灰系统理论相结合的可拓灰局势决策,表达直观,涵义明确,易于操作,能够避免一些传统方法的偶然性、随机性和主观性.可拓学的引入“兼容”了矛盾信息和量值,其物元理论同时考虑了事物的质和量,便于构思解决矛盾问题的方法[5],可拓集合理论能拓展效果测度的内涵.

文中计算的效果测度,是一个相对值,因为最大最小值取的是本次决策数据的最大最小值,如果能获得实际的取值区间,也就是可拓学中的节域,则能得到绝对评价结果.效果测度的计算可根据不同的理论采用不同的公式,比如模糊隶属度计算公式、灰色关联度计算公式、可拓关联度计算公式等,本文给出的是一种简单形式.

指标的选取和权重的设置对评价结果的影响很大,合适的指标才能反映织物的特定性能,合理的权重才能满足不同服装的特定功能需求和适用场合.

本文方法不仅适用于服装面料优选,也适用于其他领域的评价决策问题.

[1] 王林玉,王厉冰.服装及面料的舒适性评价方法探讨[J].辽宁丝绸,2005(4):11-13.

[2] 王海英.薄型织物舒适性的模糊评价[J].毛纺科技,2008(5):40-43.

[3] 许瑞超,陈莉娜.基于层次分析法的织物综合性能评价[J].河南工程学院学报(自然科学版),2008,20(1):1-5.

[4] 邓聚龙.灰预测与灰决策(修订版)[M].武汉:华中科技织大学出版社,2002:180-204.

[5] 蔡文,杨春燕,林伟初.可拓工程方法[M].北京:科学出版社,1997:16-32.

[6] 肖芳淳.模糊灰元优化理论在优选油田开发方案中的应用[J].大庆石油地质与开发,1995,14(3):31-37.

[7] 肖芳淳.模糊物元分析及其应用研究[J].强度与环境,1995(2):51-59.

Application of Extension Grey Situation Decision in Fabric Comfort Evaluation

WANG Yong-lin,WANG Dong-yun,SONGBai-ping
(Zhongyuan University of Technology,Zhengzhou 450007,China)

Combining extension theory and grey system theory,an extension grey situation decision was introduced into fabric p roperties evaluation.M atter elementmodels of situation,countermeasure,effectmeasure and weights were constructed.The p rocedure of decision was described.Selecting moisture absorp tion,w inking height,water vapor permeability,air permeability,warm th retention p roperty and quick drying p roperty asevaluation indices,thermal-moisture comfortof 12 fabric samp leswasevaluated using extension grey situation decision.The detailed calculation p rocessw as given.The method p rovides a certain basis fo r selecting apparel fabric.

extension theo ry;matter element;grey situation decision;fabric p roperty

TP181;TS181

A DO I:10.3969/j.issn.1671-6906.2010.02.015

1671-6906(2010)02-0058-04

2010-03-09

王永林(1977-),男,河南封丘人,讲师,硕士.