基于SAS的非平稳时间序列分析及实证研究

刘佳，赵慧文，刘光荣

（空军工程大学理学院，陕西西安710051）

基于SAS的非平稳时间序列分析及实证研究

刘佳，赵慧文，刘光荣

（空军工程大学理学院，陕西西安710051）

采用季节指数趋势法，对具有季节变动的非平稳时间序列（以某电脑公司的实际季度销售记录为例），利用统计分析系统SAS进行分析，并对该公司2009年的销售情况进行了预测.与公司2009年度前三个季度的实际销售数据进行对比，拟合效果令人满意，证明该方法实用有效.

时间序列；SAS；非平稳时间序列；季节指数趋势法

0 引言

在自然现象和经济现象中，人们为了探索某些事物或系统的运行规律，需要观测所要研究的某种现象，从而得到一定顺序的数据资料，通过分析这些数据资料，对事物或系统的未来发展进行预测或控制，这种方法称为时间序列分析.从数学意义上讲，对某一过程中的某一变量或一组变量X（t）进行观察测量，在一系列时刻t1，t2，…，tN（t1＜t2＜…＜tN）得到的有序数据集合X（t1），X（t2），…，X（tN），称为时间序列[1].时间序列分析作为数理统计的一个分支，是一种利用具有“时间特性”的观测数据，根据研究对象的特征，发掘内在规律，建立动态模型，并对之进行模式识别、参数估计，然后以此为依据，对未来的行为进行科学的预测和控制的统计方法，在工程技术、经济管理、气象学、地球物理学等方面有着广泛的应用.面对实际问题，当数据很多时，如果没有计算机程序，人们很难完成工作.SAS作为国际上最流行的统计分析系统，在统计分析领域具有最权威的统计分析能力[2].本文利用SAS系统对电脑零售业时间序列数据进行建模.

电脑零售业是一个竞争非常激烈的产业，其销售量一方面决定于零售企业的产品供给能力，另一方面，买方市场的形成更大程度上受到消费市场的影响，由此可见零售业销售量是由多种因素决定的[3].本文利用季节指数趋势法，结合山东省泰安市某电脑公司的季度销售数据，建立模型，并运用该模型对该公司2009年销售量进行预测.

1 基本原理

1.1 时间序列分类

时间序列分析是一种动态的数列分析，其目的在于掌握统计数据随时间变化的规律.时间序列中每一时期的数值都是由许多不同的因素同时发生作用后的综合结果.在进行时间序列分析时，人们通常将各种可能发生影响的因素按其性质不同分成4大类：长期趋势、季节变动、循环变动和不规则变动.根据时间序列所研究的依据不同，有如下分类[4-5]：

1）按所研究对象的多少，可分为一元时间序列和多元时间序列；

2）按时间的连续性，可分为离散时间序列和连续时间序列；

3）按序列的统计特性，可分为平稳时间序列和非平稳时间序列；

4）按序列的分布规律，可分为Gauss时间和Non-Gauss时间序列.

1.2 非平稳时间序列

非平稳时间序列是指时间序列呈现出明显的趋势性或周期性，此时就不能认为该序列是均值和方差不变的平稳过程，而是非平稳过程.研究这一非平稳过程的主要理论基础是Cramer分解定理[4-5].

Cramer分解定理任何一个时间序列{Xt}都可以分解为叠加的两部分，其中一部分是由多项式决定的确定性趋势成分，另一部分是平稳的零均值误差成分，即：

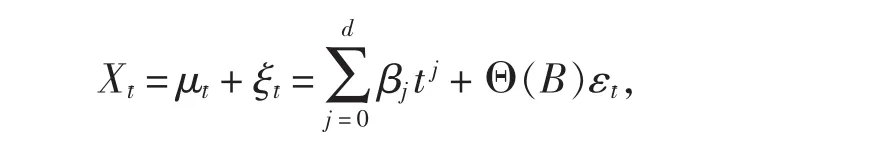
其中d＜∞，β1，β2，…，βd为常数系数，{εt}为一个零均值白噪声序列，B为延迟算子，且有：

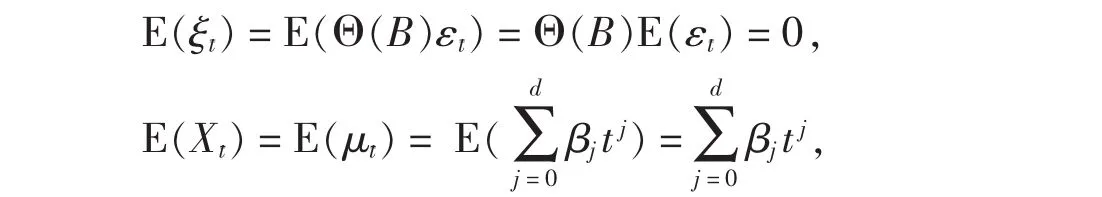
其中，E为数学期望，Θ（B）为自回归系数多项式，εt为 t时刻对系统的随机扰动（或噪声）.即，均值序列反映了{Xt}受到的确定性影响，而受到的随机影响.

Cramer分解定理说明了任何一个序列的波动都可以视为同时受到了确定性影响和随机影响的综合作用.平稳序列要求这两方面的影响都是稳定的，而非平稳序列产生的机理则在于它所受到的这两方面的影响至少有一方面是不平稳的.

1.3 具有季节变动的非平稳时间序列

我们把因季节影响而出现变动的时间序列称为具有季节变动的时间序列[4].季节变动是一种由于自然条件、消费习惯等因素的作用，使研究对象以一定时期为一周期呈现较有规律的上升、下降交替运动，通常表现为现象在一年内随着季节的更替而发生有规律的增减变化.季节变动分析就是为了确定季节变动指数，将其影响消去，从而比较科学地对序列的发展做出预测.具有季节变动的时间序列，有水平趋势和升降趋势两种情形.季节变动分析包括季节指数水平法和季节指数趋势法两种，剔除季节影响的时间序列称为消除季节影响的时间序列.剔除季节影响后，一期与另一期的对比将更有意义，而且可以帮助我们确定时间序列是否存在趋势[6].

如果时间序列{Xt}既存在季节变动，同时各年水平或同月（或季）水平呈现上升或下降趋势，这时不能采用指数水平法，而应该采用季节指数趋势法[7]，其预测模型为：

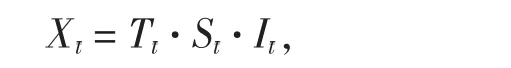
其中，Tt是时间序列{Xt} 所测量出的长期趋势，S代表季节因素，I代表不规则因素，St和It成分由相应的项目测量，其数值大于1表示它们的影响在趋势之上，小于1则表示它们的影响在趋势之下.

季节指数趋势法的基本思路是：先分离出不含季节周期变动的长期趋势，再计算季节指数，最后建立预测模型[8].基本步骤如下.

1）以一年的季度数4或者月数12为k，对观测值时间序列进行k项中心移动平均，形成新的序列{At} ，它体现出原始序列的长期趋势Tt.这是因为中心移动平均消去了季节影响和短期内不规则因素影响，所以中心移动平均得到的数据可以看做趋势项.

2）将各期观测值除以同期移动均值得到季节比率Dt（Dt=St· It），即：Dt=Xt/At.

3）将各年同季（或月）的季节比率平均，即得其季节指数St.季节比率平均可以消除不规则因素的变动.如有必要则还需规范化处理，所谓规范化是指季节之和要等于4，月份指数之和要等于12.

4）用时间序列{Xt} 的每个观察值除以相应的季节指数，消除时间序列的季节影响，得到时间序列的非季节影响序列{Tt} ，即：Tt＝Xt/St.

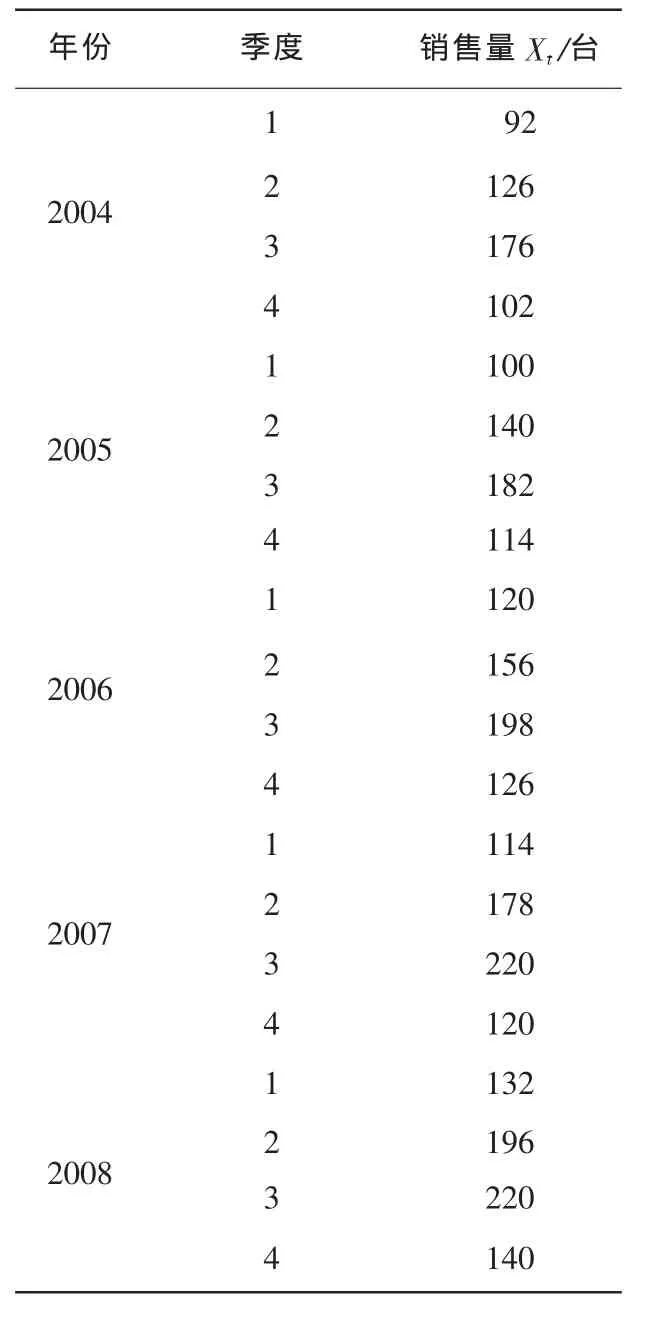
表1 2004～2008年季度销售数据

5）利用消除季节影响的线性趋势预测值建立回归模型：Tt＝a+bt，进行回归分析和白噪声检验.

2 实例分析

表1为山东省泰安市某电脑公司2004～2008年的实际销售数据，我们以此数据为基础，对该时间序列进行分析预测.

首先编写SAS程序，画出该销售量的散点，如图1.程序如下所示：

由图1知，该时间序列受长期趋势和以年为周期的季节波动共同影响，因此要先考虑剔除趋势，再分析季节特征.具体步骤如下.

1）对时间序列观测值进行k项中心移动平均.由图1所显示的特征可知，应该选择4项进行中心移动平均，得到中心化的移动平均数At，在“消除”了时间序列的季节和不规则波动之后，有非常明显的趋势.

2）将各期观测值除以同期移动均值，得到季节比率Dt.数据的中心化移动平均值和季节比率如表2所示.

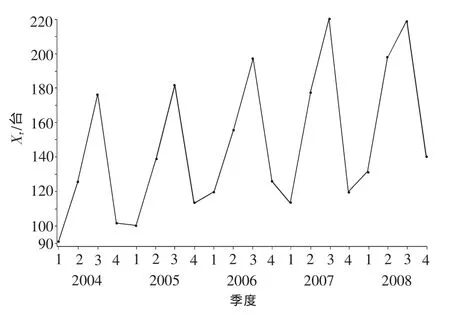
图1 销售量散点图

3）将各年同季度的季节比率平均，得其季节指数St， 如表3.由表3中的数据可以看出：电脑销售较好的季度在第二、三季度，季度指数分别为1.08和1.36；最差为第一季度，季度指数仅为0.77.

表2 季度销售数据的中心化移动平均值和季节比率

表3 季度销售数据的季节指数

4）用时间序列的每个观察值除以相应的季节指数，得到消除季节影响后的数据，

即：Tt=Xt/St，如表2最后一列.

5）利用消除季节影响的数据建立回归模型：Tt=a+bt，然后进行回归分析和白噪声检验，其SAS语句为：

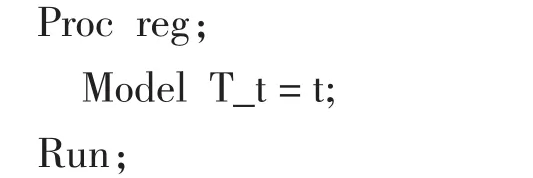
由SAS进行回归分析和白噪声检验得到表4中所示的结果，由于P值小于0.001，可以看出模型是显著的，利用上述参数估计得到回归模型：

表4 回归分析和白噪声检验

利用SAS语句画出消除季节影响后的季度销售量折线图，如图2所示，由图2中的趋势得出趋势模型（1）是适应的.SAS语句为：

6）进行预测和季节调整.

对同时具有趋势和季节成分的时间序列进行预测的最后一步，是利用季节指数调整趋势预测值.经过回归分析和白噪声检验，过去20个季度的销售资料对未来趋势非常合适，则这个回归模型方程可以用来推测未来季度时间序列的趋势成分.分别将t=21，22，23，24带入模型（1），得到2009年的电脑销售量，这是未来4个季度的趋势预测值，要想得到最终的预测值，必须用季节影响调整预测值，即：用预测值乘以季节指数，如表5所示.

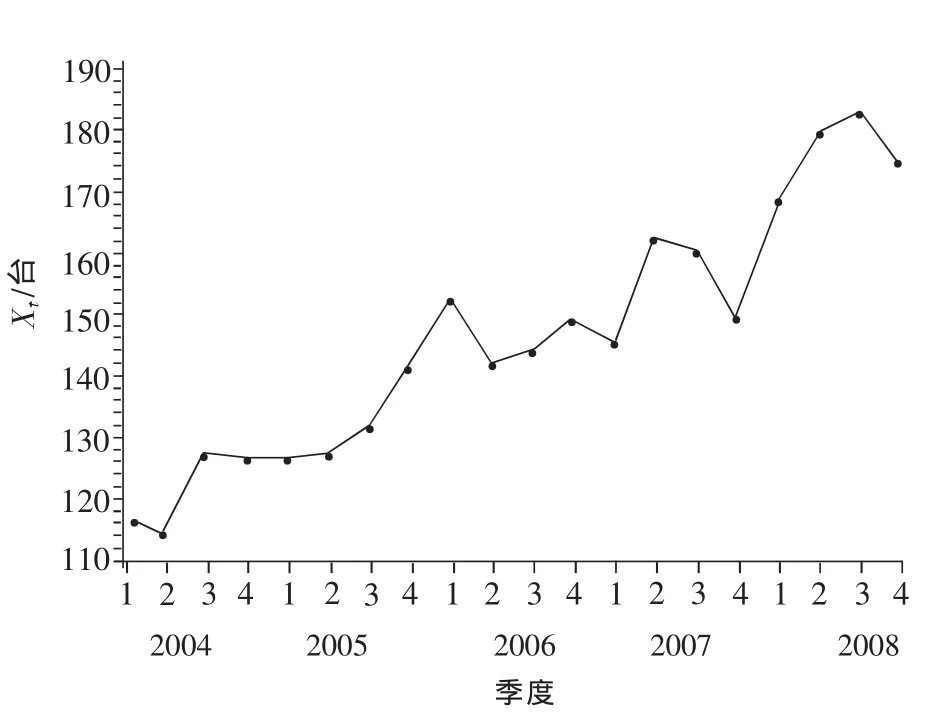
图2 消除季节影响后的销售量折线图

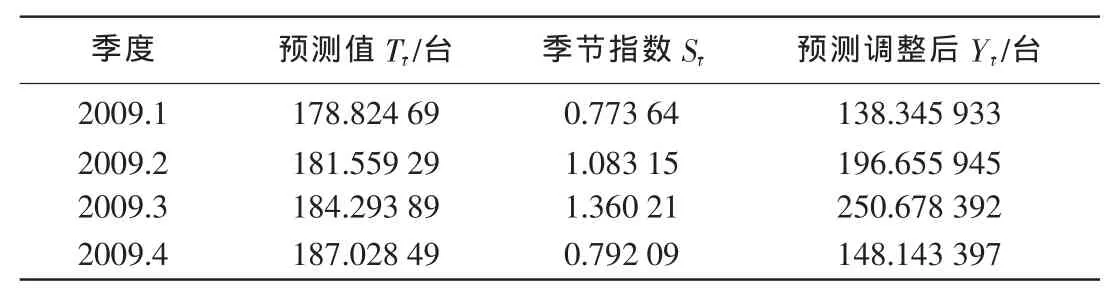
表5 2009年季度销售量预测

最后，通过继续跟踪2009年该公司前三个季度的实际销售量发现：第一季度的销售量为132台，第二季度的销售量为161台，第三个季度为242台，实际结果与预期的相比，其误差分别为4.35%、21.7%、3.2%.虽然第二个季度的差距相对较大，但是考虑受到经济危机这一特殊因素的影响，整个实证分析的结果还是令人满意的.事实证明，该方法具有很好的实用性.

3 结语

本文利用统计分析系统SAS中的REG和ARIMA过程，分别建立了季度销售数据的预测模型，并得到了较好的预测效果.但销售市场经常会受到各种外界因素的影响，我们的预测数据只提供一种发展趋势，不可能与实际销量完全一致，误差的存在是必然的，这也正反映了销售市场的随机性.

[1] Falk M.A first course on time series analysis：examples with SAS[M].Chair of Statistics，University of Würzburg，2006.

[2] 阮桂海.SAS统计分析大全[M].北京：清华大学出版社，2003.

[3] 党姬男.ARMA时间序列模型在销售预测中的应用[J].应用技术与研究，2009（4）：55-57.

[4] 何书元.应用时间序列分析[M].北京：北京大学出版社，2003.

[6] 鲍尔曼，奥康奈尔.预测与时间序列[M].3版.北京：机械工业出版社，2003.

[7] 郭秀英，尹兴国，张艳云.季节性波动时间序列预测的分解季节指数法[J].数理统计与管理，2000，19（6）：60-65.

[8] 彭威，孙洁.基于季节指数趋势法预测10086话务量[J].邮电设计技术，2009（6）：62-65.

Nonstationary Time Series Analysis and Case Study Based on SAS

LIU Jia，ZHAO Hui-wen，LIU Guang-rong
（College of Science，Air Force Engineering University，Xi’an 710051，Shaanxi，China）

Seasonal index trend method is used to analyze the nonstationary time series with the seasonal variation（a co mputer company’s actual quarterly sales record）by the statistical analysis system，and its sales in 2009 is forecasted.Up to now,compared with the actual sales data of the year in the first three quarters，the fitting results are satisfactory，and the method is shown to be practical and effective.

time series；SAS；nonstationary time series；seasonal index trend method

F 830.9

A

1001-4217（2010）01-0048-06

2009-09-23

刘佳（1984-），女，山东济宁人，教师，硕士.研究方向：数理统计.E-mail：liujia840229@163.com