函数性主成份分析的思想、方法及应用

靳刘蕊

(河南财经学院 统计学系，郑州 450002)

与多元统计分析中的多变量数据相比,函数性数据分析面临着更大的“维度灾”。函数性主成份分析能起到降低维度的作用，可以用来探索函数性数据资料的变异性，例如曲线的重要变化形式、曲线类型、代表特定函数的典型形态等。文章对函数性主成份分析的思想、方法进行了详细阐述，并将其应用于国家财政主要支出项目的变化模式的探索。

函数性数据；主成份分析；降维；主要变化模式

0 引言

函数数据分析是从函数角度对数据进行分析，把函数数据看成单个整体，表示为光滑曲线或连续函数ui(t)（i=1，2，…，n），其中n表示观测对象（曲线）的个数，t可以表示时间，也可以表示时间以外的其它变量。当t表示时间时，函数ui(t)的观测序列即为时间序列。实际情况中，关于ui(t)的信息是在有限个点（Ti）上收集的，因此观测数据向量可表示为yi=(yi1，…，yiTi)'。函数数据分析的基本统计模型为：

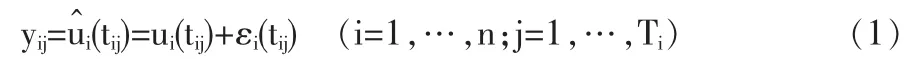
这里，对于所有的观测对象i=1，…，n，不要求它们的观测点tij和观测次数Ti相同。

在多元统计分析中，多变量统计数据是在同一时期或时点上对每一个观测对象观测多个变量的数据信息，为了使分析简化，通常把大量的原始变量综合为少数几个综合变量。多元主成份分析就是把多个变量转化为少数几个综合变量的一种通常适用的统计分析方法。在函数性数据分析中，函数性变量记录了每一个观测对象的同一个变量某个区间上很多个时刻的数据信息，如果将函数性数据的变量看作是与多元数据对应的时间（不变因素），而时间看作与多元数据对应的变量（变化因素），则发现函数性数据分析面临着更大的“维度灾”。基于这种特点，可以将多元主成份分析技术引入函数性数据分析中，称为函数性主成份分析（FPCA）。根据对观测对象测度变量的个数，函数性主成份分析可分为一元函数性主成份分析和多元函数性主成份分析。

1 一元函数性主成份分析的基本思想

在传统的多元统计分析中，对N个观测对象的p个观测变量 xi1，xi2，…，xip进行观测，观测矩阵 X为 N×p矩阵。 多元主成份分析采用简单的线性组合方法将这p个变量综合成一个综合变量，即

其中 βj为加权系数，β=(β1，β2，…，βp)'，x(xi1，xi2，…，xip)'。 fi的值称为第i个观测对象的主成份得分。记fk为x1，x2，…，xp的第k主成份，βk为第k主成份的加权系数，V为方差矩阵，可以证明观测变量p个主成份的加权系数向量βk分别为V的 p 个特征向量，k=1，2，…，p，即满足

在函数性数据背景下，函数值xi(s)（s∈T）对应于多元主成份分析中的多变量数据xij（j=1，…，p），但 s是连续的而 j是离散的，i=1，2，…，N。将区间T上的x(s)综合为一个综合变量的方式为：

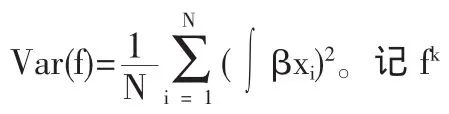
可以证明，函数性主成份的权重函数β（s）满足以下特征方程

则（6）式可表示为

可见函数性主成份分析的特征方程与多元主成份分析的特征方程相似，不同的是（3）式中的β为向量而（8）式中的β(s)为函数。另外一个重要的区别在于其特征值及对应特征向量的最大对数。多元主成份分析中观测变量的个数p决定了（3）式的特征值及特征向量的最大对数为p，进而满足约束条件的主成份的最大个数为p；函数性主成份分析中x(s)是无限的，观测对象的个数N决定了协方差算子V的秩为N-1，因此（8）式的非零特征值的最大个数为N-1，进而满足约束条件的主成份的最大个数为N-1。

当马老师给我描述李之恒家里多穷，他是多么努力，多么有出息的时候，我走神了。如果现在叫我去努力回忆李之恒是个什么样的人，我眼前浮现的形象却是我大学一个室友的模样。

函数性主成份的选取思想与多元主成份的选取相同，根据所研究问题的需要确定累积贡献率，然后选择合适的K使得达到所确定的累积贡献率，一般要求累积贡献率不小于85%。

2 一元函数性主成份的求解

由前面的分析过程可知，函数性主成份分析问题就是求解（6）式的特征值和特征函数问题。一种求解策略就是将连续的函数性特征分析问题转变为近似等价矩阵的特征分析问题。求解的一般步骤如下：

第一步，对观测得到的曲线进行曲线套准、标准化（xi(s)-等初步处理，得到的曲线记为。

第二步，对函数进行离散化处理，或进行基函数展开，或采用一般的数值积分方法，找到近似等价矩阵并求解其特征值和特征向量，再根据特征向量求解权重函数β(s)。

最简单的离散化方法就是在区间T上等间隔地取n个点sj，各点对应的函数值为，表示为 N×n矩阵X*，其样本方差记为V，从而问题转变为n个变量的多元主成份分析：

其中，对应于特征值λ的特征向量u为n维向量。由于n可能比N大，所以不采用n×n矩阵V求解（9）式，转而通过求X*的SVD UDW'可以得到V的特征值λ及其对应的特征向量u。再将求得的向量u转化为特征函数β(s)。令，然后对特征向量采用任一种合适的插值方法来计算特征函数的近似形式。

基函数展开法是对函数xi进行基函数展开，即

问题转化为下面所示的等价对称矩阵的特征分析问题：

解得u之后根据b=W-1/2u计算 b，将b代入（11）式即求得主成份权重函数β(s)。

为了避免计算得到的主成份的权重函数β(s)可能会比较粗糙，从而导致主成份分析结果的可解释性降低，需要在函数性主成份分析过程中引入平滑方法，施加某种正则化，从而得到较平滑的主成份权重函数。常用的方法包括：用粗糙惩罚法对主成份进行平滑；用粗糙惩罚法对原始数据进行平滑和逐步粗糙惩罚法。

第三步，将求得的 βk(s)代入（4）式可计算第 i个观测对象在第k主成份上的得分。

3 多元函数性主成份分析

在客观现象中，一种现象的数量变化总是与特定的其它现象的数量变化紧密联系，这多个变量的变动之间往往存在着一定的规律。针对相对于同一个变量（例如时间t）测度的、计量单位相同的多个函数，可以用主成份分析来研究它们之间的联立变动。当对N个观测对象测度P个函数变量x1(s)，x2(s)，…，xp(s)时，记 x(s)=(x1(s)，x2(s)，…，xP(s))'。多元函数性变量的主成份f定义为：

其中，主成份 f的权重函数 β(s)=(β1(s)，…，βp(s))'为 P 维向量函数，βp(s)表示 xp(s)的变动权重，p=1，…，P。 记为xp(s)的协方差算子，为 xp(s)和 xq(s)的交叉协方差函数，p，q=1，…，P；p≠q。 有。 类似的，多元主成份分析问题可转化为特征方程系统Vβ=λβ的求解问题，实际计算方法与一元情形下相似。

4 我国财政主要支出项目的主成份分析

从国内外财政的具体实践上来看，财政支出结构受社会资源配置总体的直接制约，其发展变化还与经济发展阶段、经济发展程度以及该阶段政府所追求的主要经济政策目标密切相关。财政支出结构的变化是对经济、社会不断发展和政府之能变化的一个反映。随着经济的发展，我国的财政支出结构也发生了很大的变化。下面利用函数性主成份分析来研究我国1978～2005年的国家财政主要支出项目的发展变化趋势。

国家财政主要支出项目包括基本建设支出，增拨企业流动资金、挖潜改造资金和科技费用，地质勘探费，工、交、流通部门事业费，支农支出、文教科学卫生支出、抚恤和社会救济福利费，国防支出、行政管理费，政策性补贴支出等。利用MATLAB编写函数性分析程序，首先对数据进行平滑、描述、显示，并进行更深一步的函数性主成份分析。图1绘制出了国家财政各项主要支出项目的平滑曲线，并可根据平滑曲线求出其变化速度曲线，即一阶导数曲线。根据各财政支出项目曲线可以看出国家财政各主要支出项目在1978～2005年期间总体趋势都是增长的，但增长速度差异很大。1989年之前，基本建设支出高于其它支出项目，为财政支出最多的项目，但其增长速度慢于文教、科学、卫生支出项目，后者从1986年开始快速增长，1989年之后超过了基本建设支出，成为财政支出最多的项目。此外，行政管理费支出的增长速度也比较快，支出额逐渐接近基本建设支出额，并在2003年之后超过了基本建设支出；其次变化较大的支出项目是国防支出、支农支出、挖潜改造资金和科教三项费用和政策性补贴。相对这些项目支出而言，其它项目如增拨企业流动资金支出项目变化不大。这种支出结构的变化是符合我国国民经济的发展要求的。在改革开放初期，通过扩大基本建设支出，促进经济发展，扩大经济规模和就业机会，提高人们生产生活条件；随着经济的发展和市场机制的完善，财政可配置资源增加，国家财政加大对满足人民群众日益增长的难以通过市场机制实现的物质、文化等方面的支出，其中重要的一项就是文教、科学、卫生支出项目；此外还有国防支出和为缩小城乡差距的支农支出等。

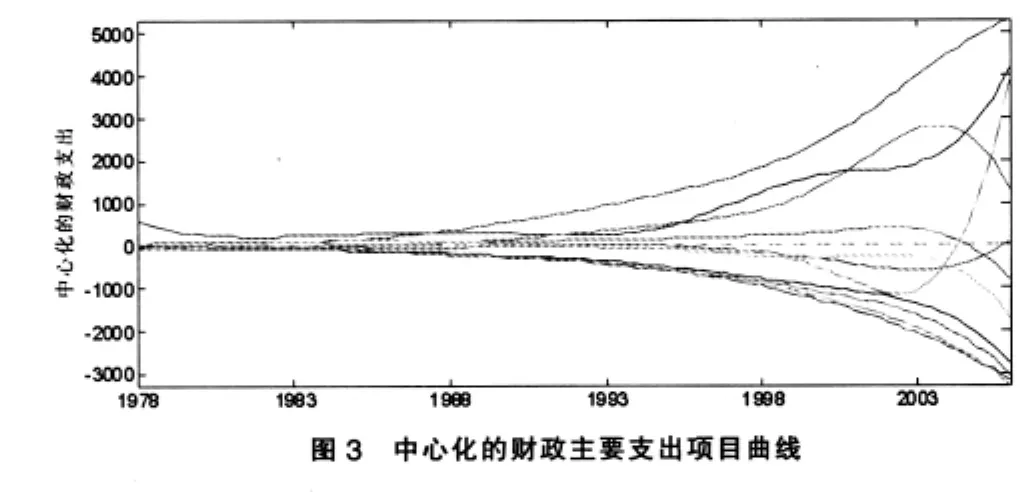
图2描述了国家财政11个主要支出项目的均值曲线和标准差曲线。从均值曲线可以明显地看出财政支出各主要项目的平均变化趋势是逐年递增的，且增长速度加快。由标准差曲线可以看出，各项目支出额之间的差异随着时间的变化越来越大。

图3显示了国家财政11个主要支出项目的中心化财政支出曲线，即从各项目的财政支出曲线中减去它们的均值曲线。该图清晰地表明各个支出项目偏离均值曲线的情况：相比较而言，1988年之前11个国家财政主要支出项目之间的差距不大，之后差距增大。其中文教、科学、卫生支出越来越高于平均水平，此外高于平均水平的支出项目有基本建设支出和行政管理费；而增拨企业流动资金，地质勘探费，工、交、流通部门事业费和抚恤和社会救济福利费越来越低于平均水平；其余项目的变化保持与平均水平大体相同。

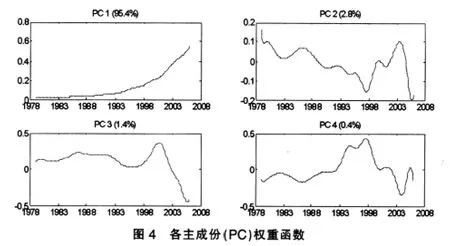
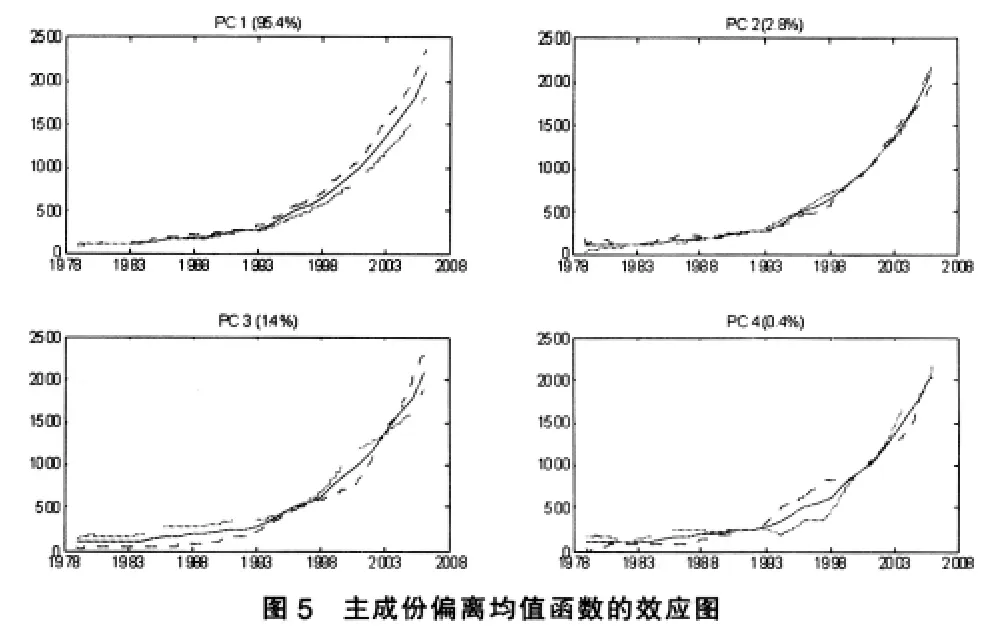
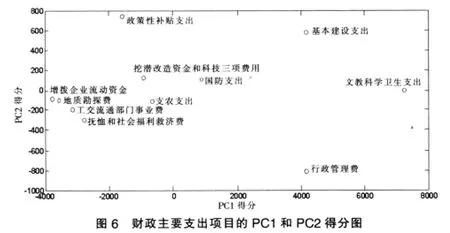
图4显示了四个主成份（PC）的权重函数。为了清晰地显示各主成份所代表的变化模式，将均值曲线、分别在均值曲线上加上和减去各个主成份权重函数合适倍数后得到的两条曲线绘制在一个坐标图中，如图5所示，分别用实线、虚线（…）和长划线（--）表示。第一主成份（PC1）解释了数据95.4%的变异，其权重函数始终为正，且随时间变化越来越大。第一主成份得分越高的财政支出项目，受到在1978～2005年期间高于平均支出水平趋势的影响越大，例如文教、科学、卫生支出，基本建设支出，行政管理费等；得分越低则说明受到低于平均支出水平趋势的影响越大，例如增加企业流动资金，地质勘探费，工、交、流通部门事业费和抚恤、社会福利救济费等。第二主成份（PC2）解释了数据2.8%的变异，其权重函数的波动表现为先下降后上升再下降，时正时负。第二主成份得分越高的财政支出项目，例如政策性补贴支出、基本建设支出等，受到如图4右上角所示趋势的影响越大，即在1978～1990年期间高于平均支出水平的程度逐渐减少，1990年之后低于平均支出水平越多，1998年之后又开始缩小与平均支出水平的差距，之后又增大缩小增大；得分越低的财政支出项目，例如行政管理费，受到与前面相反趋势的影响。图6为财政各支出项目的PC1和PC2得分图，可清楚看出它们受到PC1和PC2的影响状况。文教、科学、卫生支出主要受PC1的正向影响，几乎不受PC2的影响；基本建设支出和行政管理费同时两者相同程度的影响，不同的是PC2对基本建设支出的影响是正向的，而对行政管理费的影响是负向的；挖潜改造资金和科技三项费用、国防支出和支农支出受两者的影响都很小，反映它们在观测期间变化不大；政策性补贴支出受PC2影响有较大的波动；抚恤和社会福利救济费，工、交、流通部门事业费、地质勘探费和增拨企业流动资金等项目受PC1的负向影响比较大，与财政支出平均水平差距扩大的事实相吻合。

5 结论

与传统的分析方法相比，函数性数据分析具有其自身的优越性，它依赖较少的假设条件和较弱的结构约束，不要求不同观测对象的数据观测点和观测次数相同，不但可以实现对无限维度数据的模式挖掘，而且还可用于对非函数性数据进行分析。作为函数性数据分析的一项关键技术，函数性主成份分析能起到降低维度的作用，可以用来探索函数性数据资料的变异性，例如曲线的重要变化形式、曲线类型、代表特定函数的典型形态等，还可以用于研究多个函数之间的联动性变动。随着信息技术的发展，人们获取和存储数据的能力得到了极大的提高，需要处理越来越多的具有函数特征的数据，经济数据的函数性主成份分析方法及其应用有待进一步研究和扩展。

[1]雷钦礼.经济管理多元统计分析[M].北京：中国统计出版社，2002.

[2]朱建平.应用多元统计分析[M].北京：科学出版社，2006.

[3]朱建平,来生强.流式数据挖掘的现状及统计学的研究趋势[J].统计研究,2007，7.

[4]Ramsay,J,Silverman,B.Applied Functional Data Analysis:Methods and Case Studies[M].New York:Springer，2002.

[5]Ramsay,J,Silverman,B.Functional Data Analysis[A].Springer Series in Statistics[M].New York:Springer,1997.

[6]Rice J.A.Functional and Longitudinal Data Analysis:Perspective on Smoothing[J].Statistical Sinica，2004，14.