混沌时间序列的支持向量机预测

向昌盛，周子英

（湖南农业大学a.东方科技学院；b.资源环境学院，长沙 410128）

0 引言

混沌时间序列预测是建立在Takens[1]提出的嵌入定理和相空间重构理论基础上的，其目的是试图在高维相空间中恢复混沌吸引子。传统的时间序列预测方法，比如自回归、移动平均以及自回归移动平均的方法都属于线性的方法。而基于Takens的理论，人们已提出了许多预测混沌时间序列的非线性预测方法[2]。基于神经网络的预测方法是其中重要的一种[3]，并取得了较好的结果。但由于神经网络的结构过于复杂且难以选择，需要估计的参数相对于较少的数据样本显得太多，导致所得到的神经网络模型相对于数据容易产生过拟合，即泛化能力不够，从而使预测精度不高，在实际应用中受到了限制[4]。

支持向量机（SVM）[5～8]是一种上世纪90年代中期发展起来的基于统计学习理论的机器学习方法，是继神经网络研究之后机器学习领域新的研究热点，它具有严格的数学基础，通过寻求结构风险最小化原理来提高泛化能力，较好地解决了小样本、非线性、高维数和局部极小点等实际问题；与传统的神经网络相比，解决了在神经网络中无法避免的局部极小值问题，避免了传统神经网络拓扑结构需要经验试凑的方法。

本文拟根据某市场需求的历史数据，先估计最优嵌入维数m和时延参数τ,重构混沌时间序列的相空间来近似原系统状态空间；然后利用支持向量机方法拟合系统演化的轨道,建立混沌时间序列的预测模型；同时与传统的时间序列测试方法进行比较。

1 混沌时间序列相空间重构

混沌预测的基础是状态空间的重构理论，假设观测到的混沌时间序列为{x(t)}，t=1，2，…，N；嵌入维数为 m；时间延迟为τ，则重构相空间为：

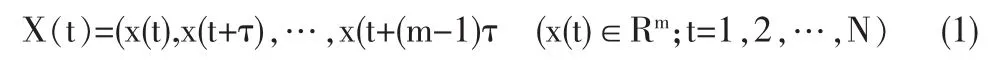
根据 Takens定理，对合适的嵌入维数 m及时间延迟τ，重构相空间在嵌入空间中的“轨线”，在微分同胚意义下与原系统是动力学等价的，这样进行相空间重构时，需要选择两个重要参数—延迟时间τ和嵌入维数m。对于无限长、无噪声数据序列，延迟时间τ的选取理论上没有限制，而嵌入维数m可以选择充分的大。实际中，由于数据长度有限并可能带噪，τ和m的选择对相空间的重构质量就尤其重要。

目前对于τ的估值，有自相关法 、互信息量法，对m的估值有假近邻法等，这些方法基于τ与m互不相关的观点，对 τ或m单独进行估值，文献[9]利用关系式wτ=（m-1）τ将 τ和m与延迟时间窗wτ联系起来，并给出了估计延迟时间窗wτ的方法。文献[10]的C-C方法利用关联积分同时优化出延迟时间τ和延迟时间窗wτ，该方法易操作、计算量小，从而在估计延迟时间τ和延迟时间窗wτ方面具有独特优点。本文采用C-C法选择τ，嵌入维数m的选取采用关联指数饱和法中常用的G-P算法[11]。

2 支持向量机的回归预测模型

回归预测又称函数估计，要解决的问题是：xi为预报因子值，yi为预报对象值，根据给定的样本数据集{(xi,yi)，i=1,2,…，k}，寻求一个反映样本数据的最优函数关系y=f(x)，如果所得函数关系是线性的，则称线性回归；否则为非线性回归。

2.1 支持向量机原理[7,12]

给定训练数据 X={(x1,y1),(x2,y2),…，（xl,yl）}⊂Rn×R，其中 xi为输入向量,yi是xi对应的输值,l为样本个数,支持向量回归的基本思想就是通过一个非线性映射Φ将数据xi映射到高维特征空间F,并在这个空间进行线性回归,即

式中ω为超平面的权值向量,b为偏置项。支持向量回归实际上就是在下述约束条件:

式中 ξi、为松弛变量，分别表示在误差 ε约束下（|yiωTΦ(xi)+b|）的训练误差的上限和下限；ε为Vapnik-ε不敏感代价函数所定义的误差。常数C＞0,它控制对超出误差ε的样本的惩罚程度。ε不敏感损失函数为：

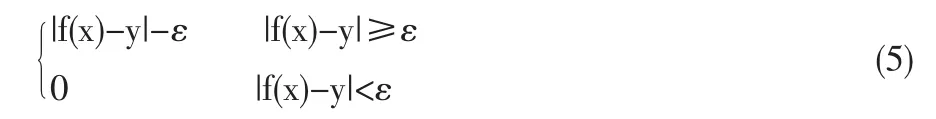
为了解这样一个优化问题,引入拉格朗日函数:

则,非线性的回归问题可以通过解式(3)的对偶问题来求解,即

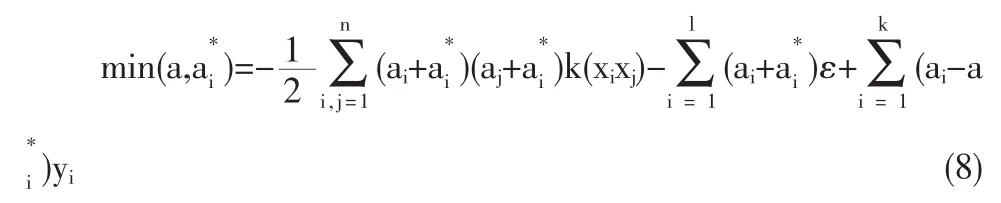
式中核函数K(xi,xj)=Φ(xi)TΦ(xj)描述了高维特征空间的内积,可以在满足Mercer条件的情况下选取。求解后得到αi和,代入式(7),并由式(2)得到回归函数:

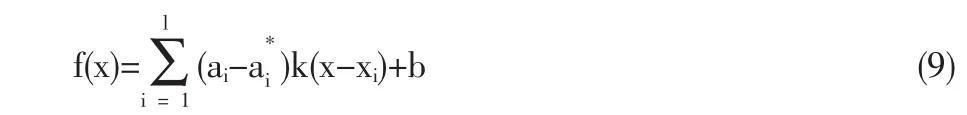
从约束条件式(3)可以看出,希望将所有的数据xi都放入|yi-[ωTΦ(xi)+b]|＜ε 中,如果 xi不在其中,则存在误差，可以通过最小化目标函数来完成。支持向量机回归通过优化式(8)避免了数据的欠拟合和过拟合,因此支持向量机是一个更为通用和灵活的解决回归问题的工具。

2.2 核函数的选取

对于具体的问题，如何选择最合适的核，一直是困扰研究者的一个难点。针对此问题本文依次采用5种常用核函数对训练集以10点叉预测并计算MSE值，取MSE最小者为最优核函数，最常用的核函数有：

线性核函数： k(xi，xj)=xixj

多项式核函数：k(xi,xj)=(xixj+1)d

径向基核函数：k(xi,xj)=exp(-γ||xi-xj||2)sigmoid核函数：k(xi,xj)=tanh[b(xixj)+c]

2.3 参数的识别

对于具体的问题，如何对参数C、g和核函数参数σ的辨识的辨识是支持向量机应用研究的热点，也是一个难点。本文采用LIBSVM2.8程序，原始变量svmscale规格化后以留一法gridregression.py寻优，自动搜索最优核函数参数C、p和g，以5个常用核函数中MSE最小者为最优核函数建模预测。

2.4 支持向量机软件LIBSVM介绍及算法实现

本文选择由台湾大学林智仁(LinChih-Jen)教授等开发设计的一个简单、易于使用和快速有效的软件包—LIBSVM，它可以解决分类问题(包括 C-SVC、nu-SVC)、回归问题(包括epsilon-SVR、nu-SVR)以及分布估计(one-class-SVM)等问题，提供了线性、多项式、径向基和sigmoid等四种常用的核函数供选择，可以有效地解决多类问题、交叉验证选择参数、对不平衡样本加权、多类问题的概率估计等。该软件包可免费通过 作 者 的 主 页 获 得 ：http://www.csie.ntu.edu.tw/～cjlin/libsvm/index.html[13]。本文在WINDOWS平台下自编C++程序调用Python2.5版本及支持Python接口的LIBSVM2.83程序包。

3 支持向量机模型在市场需求中的应用

3.1 数据

某公司经销某种产品，为了作好下一年的销售工作，该公司统计1991.7～2006.6每个月的实际销售量(单位:千件)[14]，见表1。

3.2 相空间重构

3.2.1 延迟时间确定

采用C-C法计算延迟时间τ，首次通过零点时的τ为延迟时间。从图1中可以看出，ΔS(m，t)，ΔS(t)的第一个近似极小值是4，S(t)的第一个近似零点也是4，既可以确定延迟时τ=4 作为时间序列{x1，x2，…，x180}的延迟时间[14]。

表1 月销售量表

图1 时间序列{x1,x2,…,x18}的延迟时间

图2 时间序列的嵌入维数

3.2.2 确定嵌入维数

嵌入维数的选取采用关联指数饱和法中常用的G-P算法，利用C-C法选取得到的延迟时间4。取嵌入为数m=2，3，…，对于每一个m，按照G-P算法，经计算取得一系列关于log(r)与logC(r)的值，并作出关系图2。从图2中可以看出，随着相空间嵌入维数的增加，当m=10时，吸引子的关联维数不再随着 m的增加而增加，关联维数D(m)=2.7632达到饱和，说明该销售量时间序列具有混沌性质，则选择此时对应的维数m=10为最佳相空间嵌入维数[14]。

3.2.3 时间序列系统混沌特性识别

混沌识别的方法分为定性的相图法、功率谱法和定量的饱和关联维数法、Lyapunov指数法等。根据前面的饱和关联维数法计算得到饱和关联维数D(m)=2.7632，说明该销售量时间序列具有混沌特性。

混沌系统运动的基本特点是对初值条件极为敏感，初始状态的微小不确定性将会迅速地按指数速度扩大，这种轨迹收敛或发散的速度，称为Lyapunov指数K。对一维系统来说，当K＜0时，系统具有稳定的不动点;当K=0时，系统出现周期现象;当K＞0时，系统出现混沌性质。确定Lyapunov指数的方法较多，主要有Wolf方法、Jacobian法、p-范数法和小数据量法等。本文运用改进小数据量法[15]计算得到销售量时间序列的最大Lyapunov指数为0.0021956，指数大于零，进一步说明，该序列具有混沌性质，因此上述的混沌时间序列的支持向量机预测模型可以对销售量时间序列进行预测。

3.3 混沌时间序列的预测

3.3.1 模型的建立与评价

根据τ=4，m=10重构相空间后的销售量时间序列为144个，由重构相空间嵌入相点构成训练样本集，得到用于向量学习的样本为：

前140个数据作为训练数据,后4个数据作为检验数据,由重构相空间嵌入相点构成训练样本集,根据这 144个点在相空间的轨迹，用支持向量机进行寻优，构造出一个最优模型，并根据此模型对销售量的走向进行预测。模型采用交叉验证法试检验本文方法的预测性能，以MSE作为预测性能优劣评价指标:

式中，yi为真值为预测值。

3.3.2 参比模型

参比模型包括加权零阶局域法、加权一阶局域法、指数平滑法（α=0.5）、指数平滑法（α=0.9）、神经网络，数据集的延迟时间和嵌入维都都相同的，在预测第i样本时，取前i-1个样本值合建模，以拟合MSE最小亚模型预测值作为该样本时间序列趋势分析最终预测结果（见表3）。

3.3.3 结果与分析

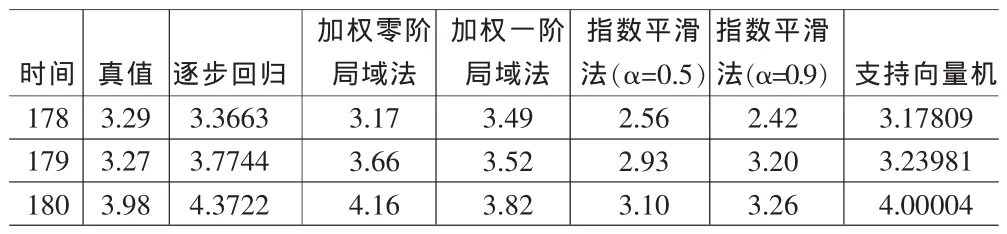
表3 混沌时间序列法的预测结果

由表4可以看出，支持向量机明显要小于其它传统方法的误差；表3表明，支持向量机的计算精度也优于传统方法。因此运用混沌时间序列方法对经济预测不仅是可行的,而且结果较好。

表4 各种预测方法的误差比较

4 结论

本文将基于统计学习理论的支持向量机和相空间重构应用到市场销售量研究中，在计算机上程序化实现。基于相空间重构的支持向量机融合了时间序列分析和回归分析，具有基于结构风险最小，非线性，避免过拟合、维数灾和局极小，泛化推广能力优异，基于MSE最小自动选择核函数、基于gridregression.py自动搜索确定最优核函数参数，操作较ANN相对简便等许多优点。实例验证表明本文的方法预测精度高，在经济学等领域有广泛应用前景。

[1]Taken S.F.Detecting Strange Attractors in Turbulence[J].Lecture Notes in Mathematics,1981,898.

[2]ZHANG Jias Hu,LI Heng Chao,Xiao Xian Ci.ADCT Domain Quadratic Predictor for Real-time Prediction of Continuous Chaotic Signal[J].Acta Physical Sinica,2004,53(3).

[3]Maguire L.P.,Roche B.,Mcginnity T.M.Predicting a Chaotic Time Series Using a Fuzzy Neural Network[J].Information Sciences,1998,112.

[4]Smola A J,Schoelkopf B.A Tutorial on Support Vector Regression[J].Statistics and Computing,2004,14.

[5]Vapnik V.The Nature of StatisticalLearning Theory[M].New York:Springer,1995.

[6]Burges C.A Tutorial on Support Vector Machines for Pattern Recognition[J].Data Mining and Knowledge Discovery,1998,2(2).

[7]Francis E.H.Tay,Lijuan Cao.Application of Support Vector Machines in Financial Time Series Forecasting[J].The International Journal of Management Science,2001,29.

[8]Dug Hun Hong,Chang Hai Wang.Support Vector Fuzzy Regression Machines[J].Fuzzy Sets and Systems,2003,138.

[9]H.S.Kim,R.Eykholt,J.D.Salas.Nonlinear Dynamics,Delay Timesand Embedding Windows[J].Physica D,1999,127.

[10]Kim H S,Eykholt R.,Salas J D.Nonlinear Dynamics,Delay Times,and Embedding Windows[J].Physica D,1999，127.

[11]Gra Ssb Er Ger P.Procaccia I Measuring the Strangeness of Strange Attractors[J].Physica D,1983,(9).

[12]Hsu C W,Chang C C,Lin C J.A Practical Guide to Support Vector Classification[R].Technical Report,Department of Computer Science and Information Engineering,National Taiwan University,2003.

[13]Chih-Chung Chang,Chih-Jen Lin.LIBSVM:A Library for Support Vector Machines[EB/OL].Software available at http://www.csie.ntu.edu.tw/～cjlin/libsvm，2001.

[14]Zhaoyanyan.Study on Method of Chaotic Time Series Forecast and Its Application in Market Requirement[D].Liaoning Technical University,2006.

[15]LU Yu,CHEN Yu-Hong,HE Guo-Guang.The Computing of Maximum Lyapunov Exponent in Traffic Flow Applying the Improved Small-data Method[J].Systems Engineering-Theory&Practice,2007,(1).