基于常规气象资料融雪模式的建立及应用

柯丹,汪玲玲,牛生杰,杨军,杨志彪

(1.南京信息工程大学大气科学学院,江苏南京 210044;2.南京信息工程大学大气物理学院,江苏南京 210044;3.湖北省气象局,湖北武汉 430074)

基于常规气象资料融雪模式的建立及应用

柯丹1,汪玲玲2,牛生杰2,杨军2,杨志彪3

(1.南京信息工程大学大气科学学院,江苏南京 210044;2.南京信息工程大学大气物理学院,江苏南京 210044;3.湖北省气象局,湖北武汉 430074)

以能量平衡方程为基础,考虑太阳短波辐射、大气和地面的长波辐射、潜热、感热传输以及下垫面的热传导等能量之间的平衡,建立了利用常规气象观测资料预测雪面温度和积雪深度变化的融雪模型。利用2009年1—3月以及2009年12月—2010年1月在湖北恩施雷达站的积雪观测数据进行模拟和验证,结果表明:该模型对于雪面温度和积雪深度都有较好的模拟效果。当下垫面导热系数λg<0.5时,下垫面对雪深的影响很小;当λg≥0.5时,积雪融化速度随λg的增大而加快,说明下垫面的热传导是影响积雪深度变化的主要因素之一。

雪面温度;积雪深度;能量平衡;融雪模型

0 引言

雪覆盖层是一种特殊的地物,积雪的温度特性和对融雪量的预测对军事、交通、水文、气象、农作物生长、环境监测及遥感等领域都具有重要作用。由于太阳短波辐射向其内部的穿透以及雪层与下方地表介质的热传导,使得它与环境间的能量交换与一般的光裸地表有所不同。

雪层内部会发生融雪并出现自由水,同时,由于夜间冷却,靠近雪表面的自由水可再结冰,这些发生在雪层的特殊现象,使得积雪模型的建立相较于其他而言要特殊和复杂。1956年,U.S.Army Crops ofEngineers[1]首次基于雪盖和环境的能量交换计算融雪量。随后,Anderson[2]、Male和Granger[3]、Morris[4]对其进行完善,形成了基于物理学能量平衡的融雪模型,通过大气的相关数据估算雪面的能量交换,就可以计算融雪量。为了利用常规气象观测数据预测融雪量,Kondo和Yamazaki[5]提出了一种基于雪覆盖层热平衡方程的简单模型,然而在此模型中,假设了雪层最下方的温度恒为0℃,即认为雪层最下方总是出现融雪的,同时,假定雪层内部由底部到表面的温度变化是线性的,这种假设可以简化雪层融雪量的计算,但用于雪层表面热辐射的模拟和预测会带来较大的误差。我国对降雪和积雪的研究主要是根据中尺度数值模式并结合相关天气背景来研究降雪的发生机制等[6-8]。

积雪层温度和深度变化是由积雪层净热辐射通量决定的,而积雪层的净热辐射通量是太阳和地球辐射通量之和。本文以能量平衡方程为基础,考虑太阳短波辐射、大气和地面的长波辐射、潜热、感热传输以及下垫面的热传导等能量之间的平衡,建立一种利用常规气象观测数据预测雪面温度和积雪深度变化的融雪模型,并利用实际观测资料进行检验,表明该模型对雪面温度和积雪深度具有较高的预报精度。

1 能量平衡方程

1.1 短波辐射(R)

到达地面的太阳短波辐射主要是受当地纬度、太阳赤纬、太阳高度角、地面反射率、大气中的气溶胶粒子浓度、空气污染程度以及云量、云状、水汽等因子的影响。Shao和Lister[9]给出:其中:S0为太阳常数(1 367±7W·m-2);f为与日地距离有关的因子,

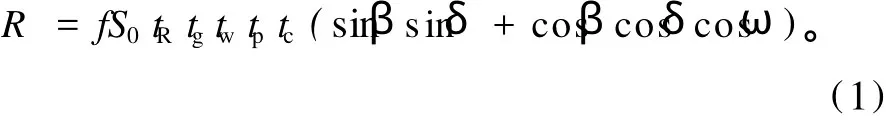
其中:N为天数。一般情况下,取f≈1.0。

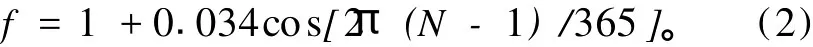
β为地理纬度;δ为太阳赤纬,

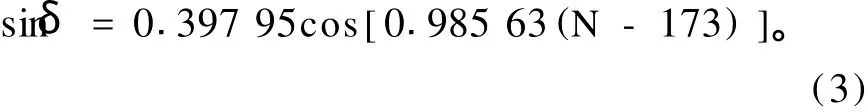
ω为时角,

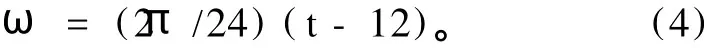
其中:t为平均太阳时(顺时针为正,逆时针为负)。

tR、tg分别为Rayleigh散射和恒量气体的吸收系数:

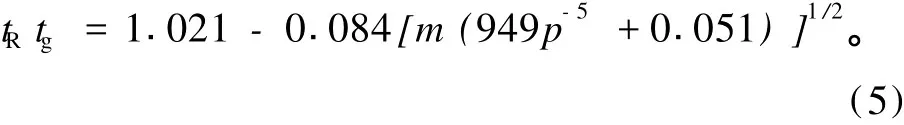
其中:p为气压;m为光学质量,

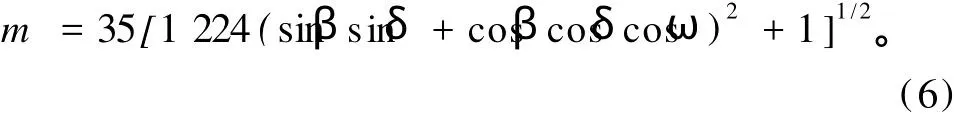
tw、tp、tc分别为水汽吸收、气溶胶及浮尘的吸收和散射、云的吸收和散射系数,

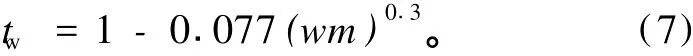
其中:w=exp[1.370 9-ln(e+1)+0.070 74Td]。e为与纬度有关的常数(1.11～3.37);Td为露点温度。

其中χ为常数(值为0.95)。

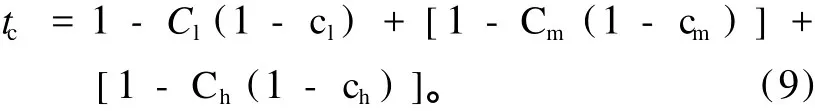
其中:Cl、Cm、Ch分别为低、中、高云云量;cl、cm、ch为低、中、高云透射率。由于在实际观测中一般没有中云量的记录,因此只考虑高云和低云的影响。Cl、Ch取值0～1,Cm=0。通过比较和调试,可取cl=0.2,ch=0.65[10]。

1.2 长波辐射(L↓-L↑)

根据Stefan-Boltzmann定律,大气长波辐射L↓为[11]

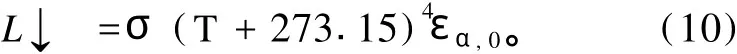
其中:T是气温(℃);σ为Stefan-Boltzmann常数(5.669 7×10-8J·s-1·m-2·℃-4);εα,0为天空显性辐射系数,

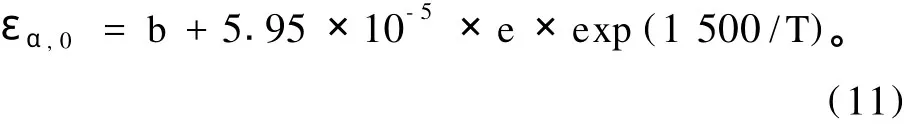
式中:e为水汽压。b为与能见度有关的常数,其取值标准为:能见度好时,b=0.69-0.01dd;能见度一般时,b=0.73-0.01dd;能见度差时,b=0.77-0.01dd。

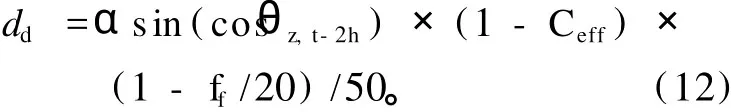
式中:θz,t-2h为天顶角(2h以后);ff为风速;Ceff为太阳直接辐射因子,

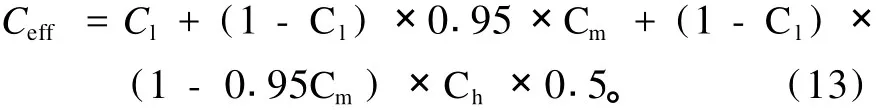
雪面的长波辐射L↑计算式为[12]:

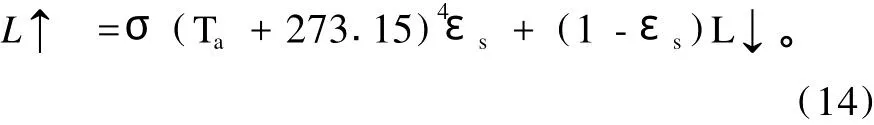
其中:Ta为雪面温度;εs为雪面辐射率(0.96)。

1.3 感热(H)和潜热(L)

感热、潜热交换项计算式为[13]:

其中:ρ0为近地面空气密度(1.29kg·m-3);cp为空气比热容(1.01×103J·kg-1·℃-1);p、Ta、v、e分别为大气气压、气温、风速、水汽压;p0为标准大气压;Lv为凝结潜热系数(2.514×106J·kg-1);CH、CE分别为感热、水汽输送系数(分别为1.81×10-3、0.15×10-3);es为雪面饱和水汽压。

1.4 能量平衡方程

根据能量平衡原理,在垂直方向一维条件下,积雪层中每一层的能量平衡方程必须满足如下条件,即进入每一层的净能量通量等于雪层内温度变化引起的能量改变量。取z坐标方向向下,单位面积(1 m×1m)积雪表面的能量平衡方程为:

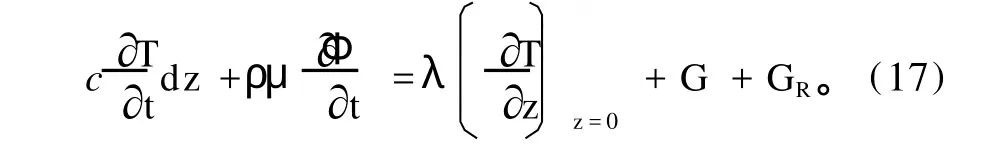
在积雪层内:

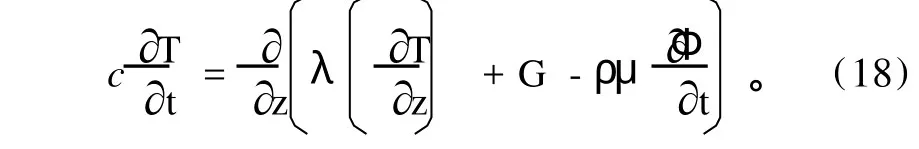
在积雪层底:

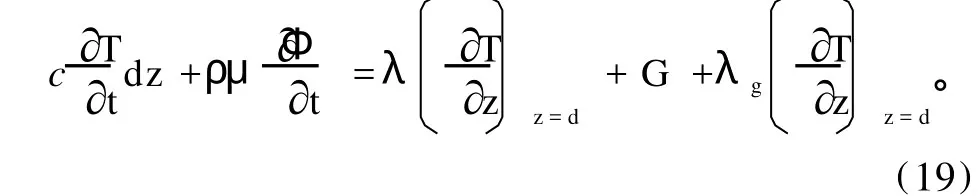
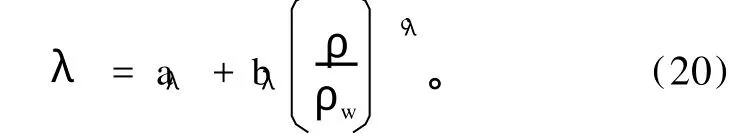
式中:aλ、bλ、cλ分别为0.021J·s-1·m-1·℃-1、2.51J·s-1·m-1·℃-1、2.0。ρw为水的密度,dz为温度升高所需的热量,其中c为积雪的平均体积热容为冰的比重(920为融化雪所需的潜热,其中μ为冰的融化潜热系数(3.35×105J·kg-1),Φ为融化雪层深度(m);λg为下垫面的热传导,其中λg为下垫面导热系数。GR为降水带来的能量。z为从积雪表面向下计算的积雪层高度(m);T为雪层温度(℃);t为时间(s);ρ为雪层密度(kg·m-3);d为雪层深度(m)。

方程(17)、(18)、(19)中有2个未知数T、Φ,必须补充一个附加的物理条件使解唯一,即:①T=0,Φ≥0;②T<0,Φ=0。

对于源汇项热通量G,在雪层内部:

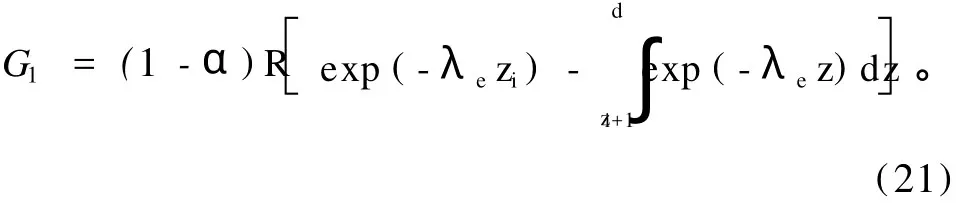
在积雪表面:

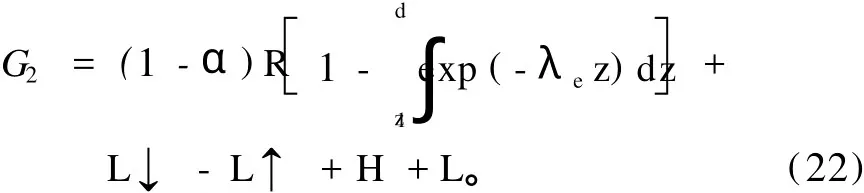
式中:α为雪面反照率;R为太阳短波辐射;λe为太阳短波辐射穿过积雪时的消光系数,

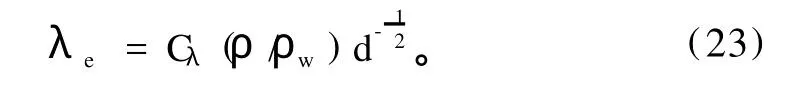
式中:Cλ为经验系数(480);ρw为水的密度。L↓-L↑为净长波辐射;H为感热交换项;L为潜热交换项。

分别采用一阶前向差分和二阶中心差分,得到方程(17)、(18)、(19)的差分形式。

所以算子Γ→C(R,R2)在Bμ(R,R2)中是连续的。类似可证Γ→C(R,R2)在Bμ(R,R2)是连续的。证毕。

方程(17)的差分形式为

式中:Δt为时间步长;Δz为深度坐标步长;n和i表示时间和深度节点。

方程(18)的差分形式为:

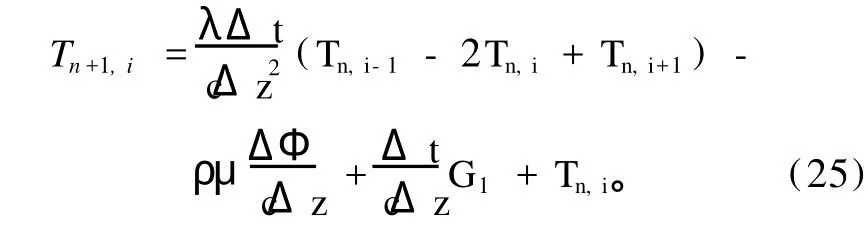
方程(19)的差分形式为:

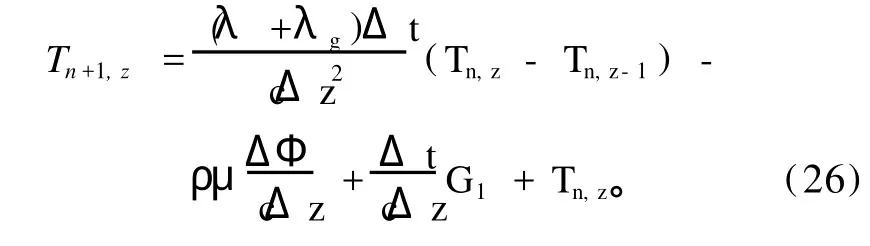
2 雪面温度和积雪深度的模拟

2009年1—3月以及2009年12月—2010年1月,在湖北恩施雷达站进行了冰冻雨雪天气的综合观测。当有积雪时,每6 h人工测量一次积雪深度,2010年1月和2009年12月的雪深观测加密为每3 h1次和每1 h1次。自动观测站观测数据中的0 cm地面温度值表示积雪底部的下垫面表面温度值。观测点下垫面为土壤,上有少量杂草,因此在模式运算中取下垫面导热系数λg为0.8W/(m·K)。

2.1 雪面温度和积雪深度的模拟

在2009年1—3月的观测中,比较明显的一次积雪过程出现在3月1—5日。3月1日降雪,3月2日雪停,3月2日08时测量的积雪深度为雪深最大值,之后融雪过程开始。本次模拟即从3月2日08时开始,至3月5日08时融雪过程基本结束。在模拟计算过程中,取计算时间步长为1h,即应用1h 1次的气象要素实况观测资料作为预报计算的气象要素场资料。以降雪停止时(本次即为3月2日08时)的雪深和雪面温度作为计算未来雪深和雪面温度的初始值。雪层划分以5.0×10-3m作为一层。

图1为2009年3月2日09时—5日08时雪面温度的模拟值与实测值随时间的变化。可以看到:雪面温度模拟值的波动范围比实测值的波动范围要小。在每日19时以后至次日09时之前,雪面温度模拟值与实测值的误差绝对值基本小于1℃,误差绝对值的平均值约0.5℃,相对误差约20%;在每日09—19时,模拟值与实测值的误差较大,最大误差达4.5℃,且在17时之前,实测值基本比模拟值高。这是因为白天雪面受太阳辐射的影响,使探头测得的雪表面温度会有所升高,因此这时观测读数不能代表真正的雪面温度。

有关积雪深度模拟值和实测值的变化见图2。由图2可见:模拟的雪深在白天大都大于实测值,而夜间则多小于实测值。这是由于本模型假设雪面温度大于0℃才会发生融雪现象,但在实际中,温度小于0℃时,也会有融雪发生,Kuhn[14]就曾指出,温度小于-10℃时都有可能发生融雪现象;其次由于夜间冷却,靠近雪表面的自由水也可能再结冰,会使雪深增加。尽管如此,模拟值与实测值的绝对误差基本小于0.5cm,多在0.2～0.3cm,相对误差也大多小于等于10%,模拟效果较好。

在2009年12月—2010年1月的观测中,12月25—26日以及1月5—6日分别有一次积雪过程,前者26日雪停,后者5日夜里雪停,两次降雪时间都较短。模拟分别从26日07时及6日00时开始。把这两次雪面温度和雪深变化的模拟(图3～6)作为对该模式的验证。结果与上述分析(图1、2)基本一致。雪深的模拟值均大于实测值,说明这两次过程中低温时积雪也有融化现象,实测的雪深要小,但模拟值与实测值的变化趋势基本一致。

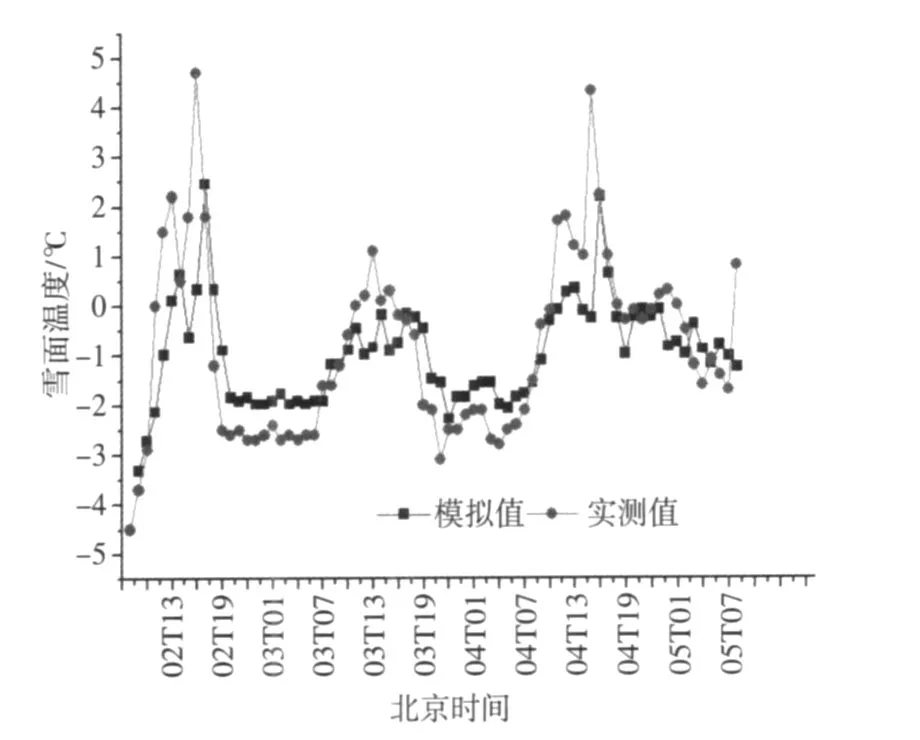
图1 2009年3月2—5日雪面温度的变化Fig.1 Variation of snow surface temperature from March2to March5,2009

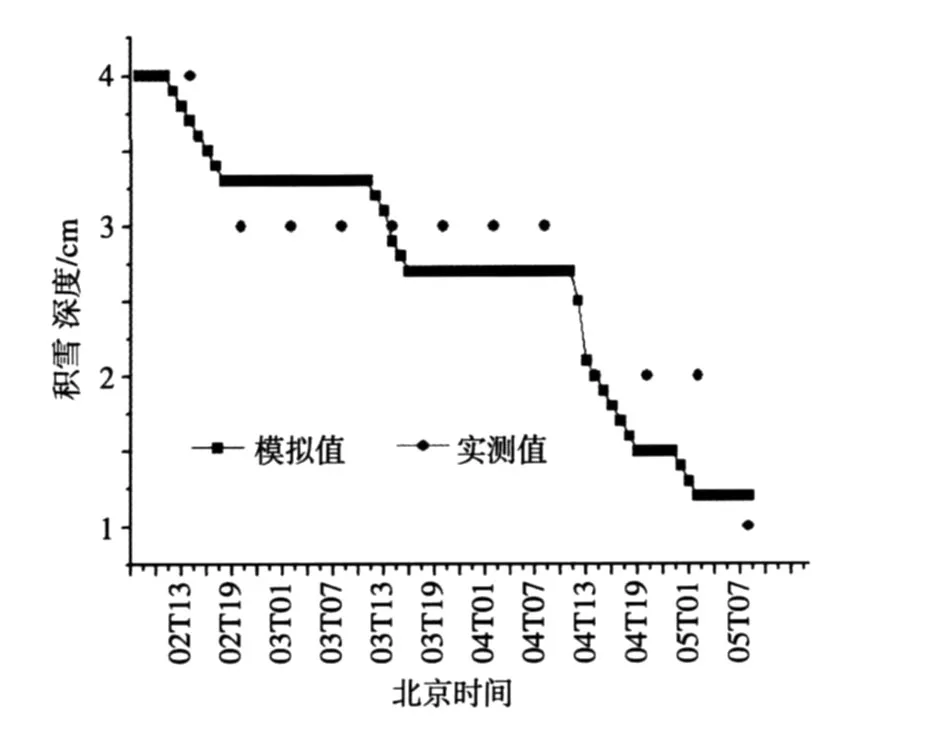
图2 2009年3月2—5日积雪深度的变化Fig.2 Variation of snow cover depth from M arch2to M arch5,2009

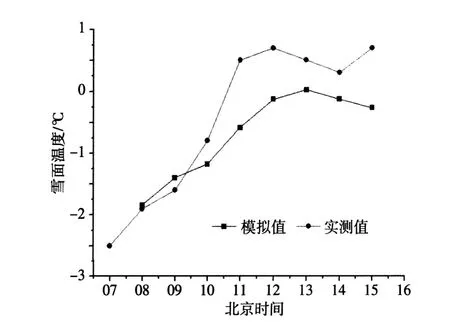
图3 2009年12月26日雪面温度的变化Fig.3 Variation of snow surface temperature on December26,2009

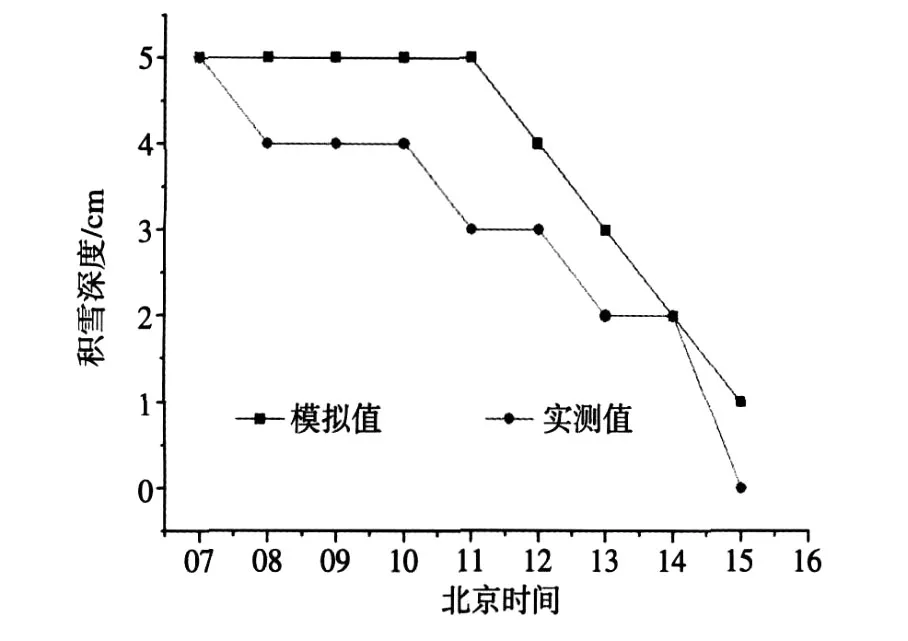
图4 2009年12月26日积雪深度的变化Fig.4 Variation of snow cover depth on December 26,2009

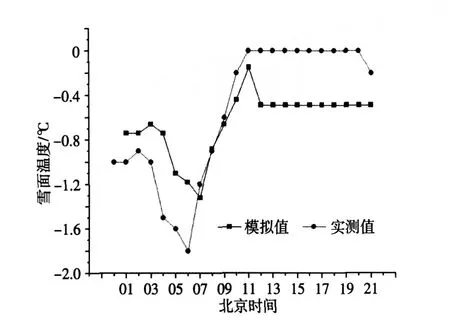
图5 2010年1月6日雪面温度的变化Fig.5 Variation of snow surface temperature on January6,2010

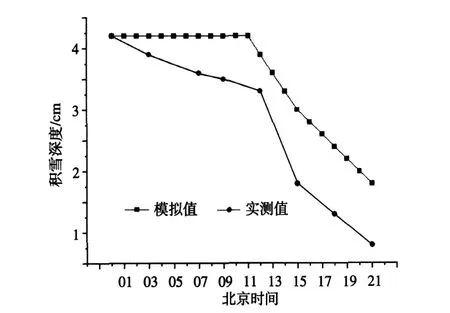
图6 2010年1月6日积雪深度的变化Fig.6 Variation of snow cover depth on January6,2010

2.2 下垫面性质对积雪深度的影响

不同下垫面的导热系数不同,由此会影响雪层底部的热传导,从而影响积雪融化量,使积雪深度的变化有所不同。分别取下垫面导热系数λg=0.05、0.1、0.2、0.5、0.8、1.0、1.5、2.0、2.5W/(m·K),模拟2009年3月2—5日的雪深变化情况(图7)。可以看出,当λg<0.5时,积雪深度的变化基本相同且较为缓慢,不同下垫面对雪深的影响很小;当λg≥0.5时,下垫面性质对雪深的变化影响明显,随着下垫面导热系数的增大,积雪融化得越来越快。对于常见的大多数下垫面,导热系数都大于0.5,如土壤的导热系数一般在1.0～2.7W/(m·K),水泥混凝土的导热系数在1.7W/(m·K)左右,因此,下垫面的热传导是影响积雪深度变化的主要因素之一。

3 小结

(1)以能量平衡方程为基础,考虑太阳短波辐射、大气和地面的长波辐射、潜热、感热传输以及下垫面的热传导等,建立了一种利用常规气象数据预测雪面温度和积雪深度变化的融雪模型。

(2)关于雪面温度的模拟,在每日19时以后至次日09时之前,模拟值与实测值之间的误差小,平均约0.5℃,模拟效果较好;在每日09—19时,由于受白天太阳辐射影响,模拟值与实测值之间的误差较大。

(3)关于积雪深度的模拟,模拟值在白天大都大于实测值,而夜间多小于实测值,但误差不大,基本小于0.5cm,相对误差基本小于等于10%,模拟效果较好。

(4)不同下垫面导热系数不同,会影响积雪深度的变化。当λg<0.5时,下垫面对雪深的影响很小;当λg≥0.5时,积雪融化速度会随下垫面导热系数的增大而加快,下垫面的热传导是影响积雪深度变化的主要因素之一。

[1] U.S.Army Crops of Engineers.Snow hydrology[M].Portland:North Pacific Division,1956:437.

[2] Anderson E A.A point energy and mass balance model of a snow cover[R]//NOAA Technical Report NWS,19,Office of Hydrology.Silver Spring,MD:National Weather Service,1976:150.

[3] M ale D H,Granger R J.Snow surface energy exchange[J].water Resources Research,1981,17(3):609-627.

[4] M orris E M.Modeling the flow of mass and energy within a snow pack for hydrological forecasting[J].Annals of Glaciology,1983,94:137-149.

[5] Kondo J,Yamazaki T.A prediction model for snowmelt,snow surface temperature and freezing depth using a heat balance method[J].Journal of Applied Meteorology,1990,29(5):375-384.

[6] 王东勇,刘勇,周昆.2004年末黄淮暴雪的特点分析和数值模拟[J].气象,2006,32(1):30-35.

[7] 杨柳,苗春生,寿绍文,等.2003年春季江淮一次暴雪过程的模拟研究[J].南京气象学院学报,2006,29(3):379-384.

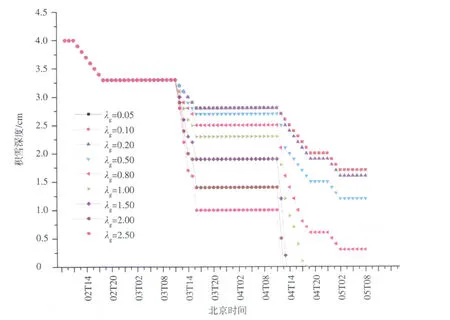
图7 不同下垫面导热系数下积雪深度的变化Fig.7 Variation of snow cover depth on different thermal conductivities of underlying surface

[8] 范元月,汤剑平,徐双柱.一次湖北暴雪天气的诊断与模拟[J].气象科学,2010,30(1):111-115.

[9] Shao J,Lister P J.An automated now casting model of road surface temperature and state for w inter road maintenance[J].Applied Meteorology,1996,35(8):1352-1361.

[10] 刘熙明,喻迎春,雷桂莲,等.应用辐射平衡原理计算夏季水泥路面温度[J].应用气象学报,2004,15(5):623-628.

[11] 王名才.大气科学常用公式[M].北京:气象出版社,1994:145.

[12] Koivusalo H,Heikinheimo M,Karvonen T.Test of a simple two-layer parameterisation to simulate the energy balance and temperature of a snow pack[J].Theoretical and Applied Climatology,2001,70(1/2/3/4):65-79.

[13] 马虹,刘一峰,胡汝骥.天山季节性积雪的能量平衡研究和融雪速率模拟[J].地理研究,1993,12(1):87-93.

[14] Kuhn M.Micro-meteorological conditions for snow melt[J].Journal of Glaciology,1987,33(113):24-26.

A Snow melt Model Based on Routine Meteorological Data

KE Dan1,WANG Ling-ling2,NIU Sheng-jie2,YANG Jun2,YANG Zhi-biao3

(1.School of Atmospheric Sciences,NUIST,Nanjing 210044,China;2.School of Atmospheric Physics,NU IST,Nanjing 210044,China;3.Hubei Meteorological Bureau,Wuhan 430074,China)

According to the equation of conservation of energy,and having considered solar shortwave radiation,atmospheric and ground long wave radiation,latent heat flux,sensible heat flux and heat conduction of ground,a snow melt model for snow surface temperature and snow cover depth with routine meteorological data is established.The observations in Enshi radar station,Hubei from January to March 2009 and from December 2009 to January 2010 have been used for simulating the process and validating the model.Results show that the model is useful for modeling the changes of snow surface temperature and snow cover depth.While the thermal conductivity of underlying surface(λg)is less than0.5,the underlying surface has little influence on the snow cover depth,but while λgis over0.5,the snow w ill thaw faster with the augmentation of λg,indicating that the thermal conductivity of underlying surface is one of major factors affecting snow cover depth.

snow surface temperature;snow cover depth;conservation of energy;snow melt model

P426.635

A

1674-7097(2010)05-0555-06

2010-04-30;改回日期:2010-07-06

科技部科技支撑计划项目(2008BAC48B01);江苏省青蓝工程云雾降水与气溶胶研究创新团队项目

牛生杰(通信作者),博士,教授,博士生导师,研究方向为云雾降水物理学,niusj@nuist.edu.cn.

柯丹,汪玲玲,牛生杰,等.基于常规气象资料融雪模式的建立及应用[J].大气科学学报,2010,33(5):555-560.Ke Dan,WangLing-ling,Niu Sheng-jie,et al.A snow melt model based on routine meteorological data[J].Trans Atmos Sci,2010,33(5):555-560.

(责任编辑:倪东鸿)