闭合气压系统中心位置指数的计算方案

王盘兴,赵辉,任律,罗璇,郭栋

(南京信息工程大学大气科学学院,江苏南京 210044)

闭合气压系统中心位置指数的计算方案

王盘兴,赵辉,任律,罗璇,郭栋

(南京信息工程大学大气科学学院,江苏南京 210044)

王盘兴等在“闭合气压系统环流指数的定义及计算”一文中定义了闭合气压系统的面积指数S、强度指数P和中心位置指数(λc,φc),并给出了它们的计算方案。但其中(λc,φc)的计算方案对低纬系统的计算存在明显误差,误差原因是原方案中的极点球面坐标系不适合低纬系统的计算。本文建立了一套原点位于搜索区Ω中心的新球面坐标系,通过坐标转换实现了低纬闭合气压系统中心位置指数(λc,φc)的准确计算。对7月南亚高压和1月蒙古高压中心位置指数(λc,φc)的实际计算表明,它既消除了低纬系统(南亚高压)(λc,φc)原计算方案的明显误差,又保持了与高纬系统(蒙古高压)(λc,φc)原计算方案计算结果的一致。因此,本文给出了适于计算任意纬度闭合气压系统中心位置指数(λc,φc)的计算方案。

闭合气压系统;中心位置指数;计算方案

0 引言

在大气环流异常与短期气候预测研究中,全年或季节出现于特定地理区域的高压、低压系统被称为大气活动中心[1]。大气活动中心的性状可以用环流指数简明扼要地描述,常用的环流指数有它们的面积、强度和中心位置等。以南亚高压、蒙古高压为例,文献[2-3]列举了它们的多种环流指数定义[4-9];可见,对同一气压系统,不同作者定义环流指数的方法存在明显差别。这给研究不同大气活动中心的相互关系带来一定困难。

文献[10]按统一的方法定义闭合气压系统的环流指数。对季、月平均气压场中具有大气活动中心性质的气压系统,均可按该方法定义一组环流指数,它包括面积指数S、强度指数P、中心位置指数(λc,φc)。对某闭合气压系统多年序列,在详细分析历史气压场的基础上容易确定其搜索域Ω(该闭合气压系统主体部分所在区域)和特征等值线f0(界定闭合气压系统主体部分的等值线);据此可以确定t年的计算域D(t),它是Ω上由t年场中f0线围成的区域。S(t)是单位半径球面上D(t)的面积;P(t)是压差(高度差)df(t)=f(t)-f0在D(t)上的积分;(λc(t),φc(t))是D(t)上df(t)场对应重力场重心所在经、纬度。(¯λc,¯φc)是该气压系统的气候中心位置指数,它是(λc(t),φc(t))以P(t)为权重的多年平均。

文献[10]借助地理坐标系(λ,φ)和一个球面曲线直角坐标系oxy完成了北、南半球500hPa层极涡环流指数S、P、(λc,φc)的计算,坐标系oxy的原点o在北(南)极点,x、y轴是λ=0、π/2的经线。S、P的计算可直接在(λ,φ)系中完成,(λc,φc)的计算则在oxy系中通过球面直角三角形计算公式[11]完成。中、高纬度多种闭合气压系统(500hPa极涡[10]、10hPa极地涡旋[12-15]、1 000hPa蒙古高压[16-17]和阿留申低压[18]等)(λc,φc)的计算结果验证了文献[10]计算方案的正确。

但是,球面三角形计算公式只对三边和小于π的球面三角形[11](注:指对单位半径球面)精确成立,上述计算方案不能用于低纬系统(λc,φc)计算。为了解决这个问题,本文引进了一个原点设在λ-φ平面上搜索区Ω中心(λ0,φ0)上的新地理坐标系(λ′,φ′),给出一个计算(λc,φc)的新方案,对7月南亚高压、1月蒙古高压(λc,φc)的计算结果,验证了它对低、高纬系统(λc,φc)的正确计算均适用。

1 S、P的定义和计算方案

(λc,φc)的计算方案涉及S、P的定义和计算,为叙述清楚,首先简要给出它们的定义和计算式。

1.1 S、P的定义

对某季、月平均气压场(位势高度场)的多年(L年)序列

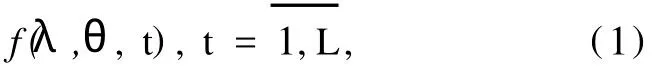
定义了t年面积、强度指数,

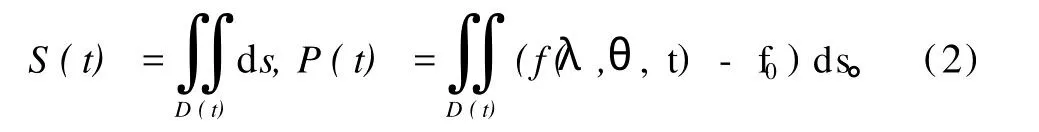
式中:λ、θ为经度、余纬,余纬θ=π/2-φ。D(t)是t年计算域,它是搜索域Ω上由t年f0线围成的区域。图1给出了2008年1月蒙古高压和1998年7月南亚高压的Ω、f0、D(t)三者关系。

1.2 S、P的计算方案

计算在单位半径球面上的地理坐标系(λ,φ)中进行。

NCEP/NCAR、ECMWF再分析资料[19-20]的要素场给出在λ-φ平面上均匀经度、余纬格点网上。其基本参数为格距Δ λ=Δ θ=π/72=2.5°,纬圈、经线等分数m=144、n=72;故格点(λ,θ)与格点序数(i,j)关系为

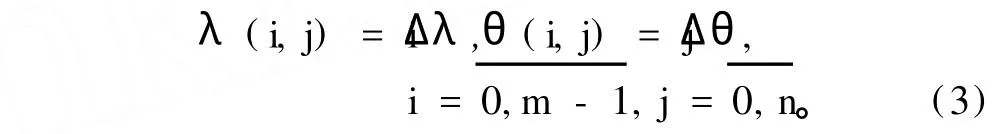
f场的多年序列的离散形式为

S(t)、P(t)的差分计算式为

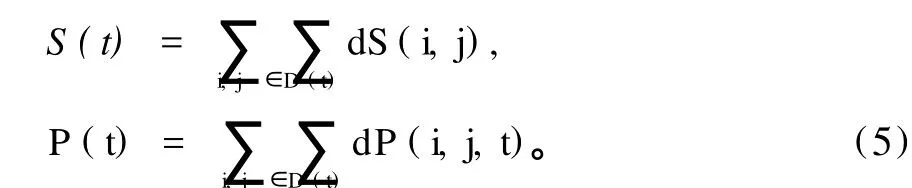
式中:dS(i,j)为(i,j)格点所在面元的元面积;dP(i,j,t)为t年D(t)上(i,j)格点所在面元上的元压差(元位势高度差)。根据文献[10],

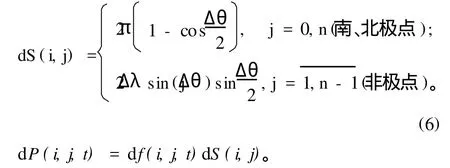
2 (λc,φc)的定义和计算方案

按文献[10],t年的闭合气压系统中心位置指数(λc(t),φc(t))是D(t)上压差场dP(λ,θ,t)=f(λ,θ,t)-f0对应重力场的“重心”位置。以r记球面上任意点(λ,θ)的位置矢量,rc(t)是球面上矢端在重心(λc(t),θc(t))上的矢量,r、rc(t)分别是从球面上选定(λ0,θ0)点出发至(λ(t),θ(t))、(λc(t),θc(t))的与大圆弧重合的矢量。则rc(t)由下积分方程定义而该系统气候中心位置指数(¯λc,¯θc)则由下式定义,

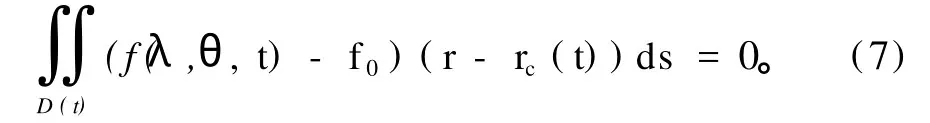
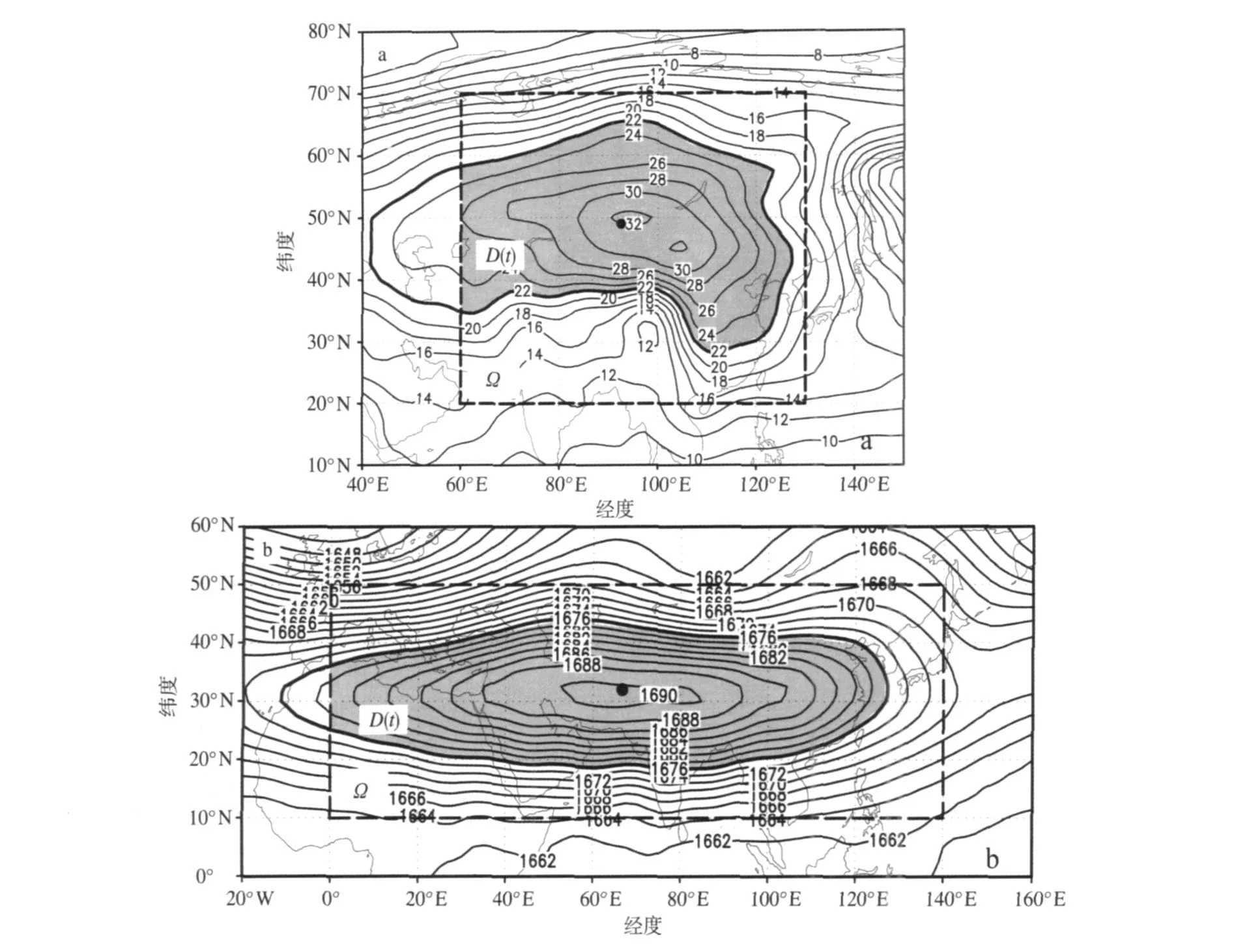
图1 闭合气压系统Ω、f0、D(t)三者关系(粗实线为特征等高线f0,粗虚线矩形区为搜索区Ω,阴影为计算域D(t);·为中心位置) a.2008年1月1 000hPa上蒙古高压(f0=22dagpm);b.1998年7月100hPa上南亚高压(f0=1 678dagpm)Fig.1 Relationships ofΩ,f0and D(t)for the closed pressure system s(The thick solid line is the typical line f0;the rectangle is searching area Ω;the shading is computational domain D(t);·is the center position) a.Mongolia Highat 1000hPa in January2008(f0=22dagpm);b.South Asia H igh at100hPa in July1998(f0=1 678dagpm)

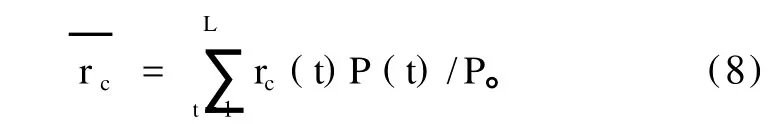
2.1 高纬度系统(λc,φc)的计算方案

为了计算t年中高纬度闭合系统的rc(t),文献[10]建立了坐标系OXYZ和oxy(图2)。OXYZ是原点在地心的三维直角坐标系,其基向量i、j、k是矢端分别位于单位半径球面上(λ,θ)为(0,π/2)、(π/2,π/2)、(λ,0)点的单位向量。oxy是原点在北极的球面曲线直角坐标系,其基向量e1、e2是矢端分别位于单位半径球面上(λ,θ)为(0,1)、(π/2,1)点的单位向量。均为标准正交基。

由图2可知,球面上任意点q的地理坐标(λ,θ)与(X,Y,Z)间的转换关系为

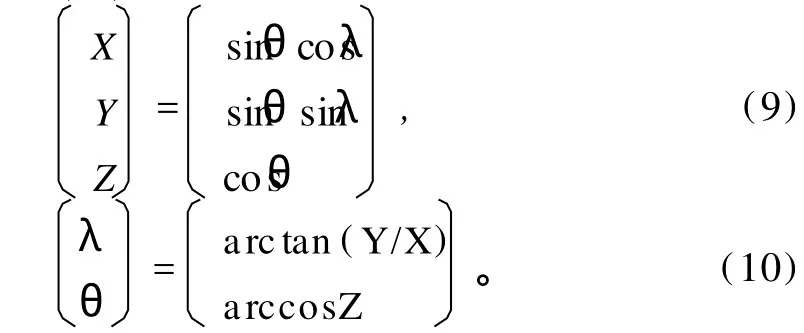
而据球面直角三角形计算公式[11],可导出点q的地理坐标(λ,θ)向球面直角坐标(x,y)的坐标转换关系(称为正变换),

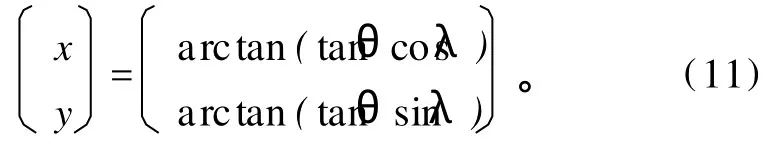
据此可将场f(λ,θ,t)转换为f(x,y,t),并在坐标系oxy中求得t年的该闭合气压系统的中心位置,

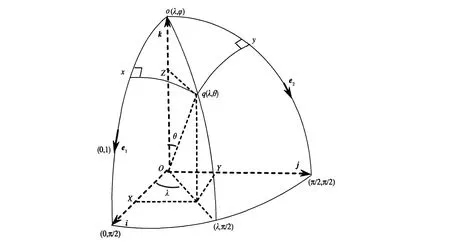
图2 地理坐标(λ,θ)与单位半径球直角坐标系OXYZ、oxy三者关系(q是球面上位于(λ,φ)的任意点,它在OXYZ中的坐标为(X,Y,Z),在oxy中的坐标为(x,y))Fig.2 Relationship of the geographic coordinate(λ,θ)and the rectangular coordinate system s OXY and oxy in an unit radius sphere(q is an arbitrary point at(λ,φ)on the spherical,corresponding to(X,Y,Z)in OXYZ and(x,y)in oxy)

而由(x,y)向(λ,θ)的坐标变换关系(称为逆变换)为

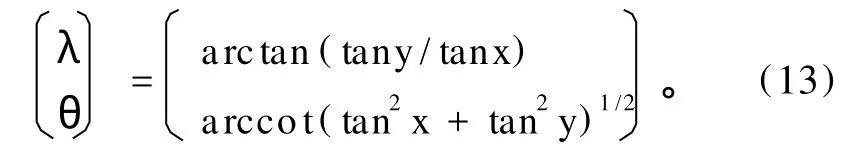
据此可将(xc(t),yc(t))转换为(λc(t),θc(t)),求得逐年分析对象的中心位置指数序列

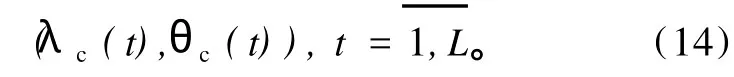
文献[10]将(2)、(12)式给出的闭合系统强度指数及位置参数多年序列

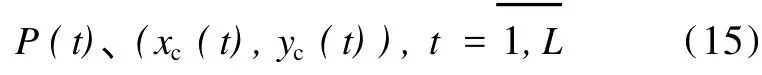
视为一个力学系统,定义了该系统的气候中心位置指数

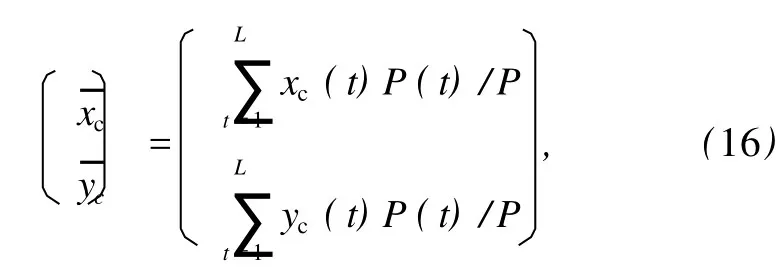
2.2 低纬度系统(λc,φc)的计算方案

闭合气压系统的搜索域Ω一般为(或可处理为)λ-θ平面上的矩形域[λw～λe,θn～θs]。这里λw、λe为Ω的西、东界所在经度,θn、θs为北、南界所在余纬(图1)。为准确计算低纬系统的(λc,φc),建立新地理坐标系(λ′,θ′),其北极点o′取在Ω的中心点(λ0,θ0)上,

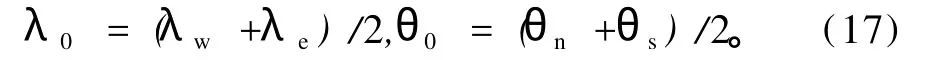
对南亚高压(图1b),λ0=70°E,θ0=60°(即φ=30°N)。经线λ′=0从o′出发沿λ=λ0经线指向南极,经线λ′=π/2从o′点出发垂直于λ=λ0经线指向东(即为与φ=π/2-θ0纬圈相切的大圆的向东部分);它们分别是新球面曲线直角坐标系o′x′y′的x、y轴。简言之,新地理坐标系(λ′,θ′)是原地理坐标系(λ,θ)绕地轴逆时针旋转λ0,再将北极点沿λ0经线南移θ0角得到。对新地理坐标系(λ′,θ′)建立相应的o′x′y′和OX′Y′Z′坐标系,它们的相互关系全同于(λ,θ)、oxy与OXYZ。

原点位于地心的直角坐标系OXYZ、OX′Y′Z′的基向量间关系为

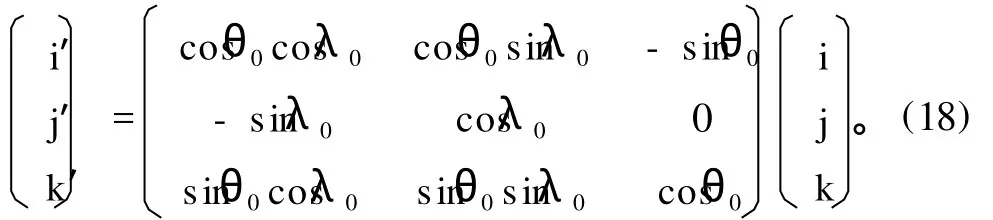
由此得球面上任意点q(λ,θ)的坐标(X,Y,Z)、(X′,Y′,Z′)间的正、逆转换关系为

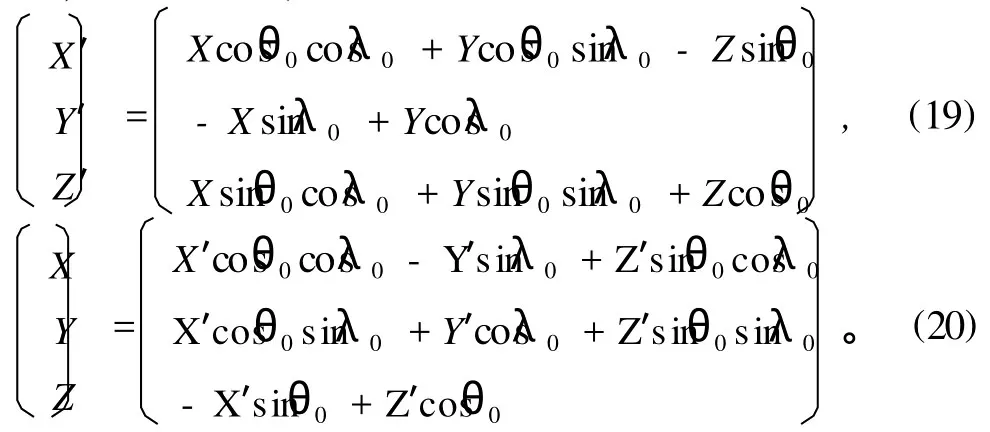
利用正转换关系(19)式,可将求(λc,φc)的问题转入新坐标系中进行。因为新坐标系的北极点(即o′)位于Ω中心,只要Ω不很大(保证计算涉及的球面直角三角形三边和不超过π),新坐标系中(λ′c,φ′c)的计算将是精确的。而(λ′c,φ′c)可经逆转换关系(9)、(20)式返还原坐标系,最终求得低纬系统中心位置指数(λc,φc)。

因(8)式中(λ0,θ0)可在整个球面域上取值(当然必须是Ω中心点),故低纬系统(λc,φc)计算方案理论上也适合于高纬系统(λc,φc)的计算,是求气压系统(λc,φc)的普适计算方案。

低纬系统(λc,φc)计算方案的流程可归结为:

1)计算(Xij,Yij,Zij)Ω、(xij,yij)Ω(据(9)、(11)式);

2)计算(S(t))t、(dSij)Ω(据(5)、(6)式);

3)计算(P(t))t、(dPij)Ω,t(据(5)、(6)式);

4)(Xij,Yij,Zij)→(据(19)式);

最后,将换算为(λc(t),换算为

3 验证

在资料、Ω、f0与文献[2,16]相同情况下,用本文(λc,φc)计算方案分别计算了60a(1948—2007年)7月100hPa南亚高压和60a(1949—2008年)1月1 000hPa蒙古高压中心位置指数,记为

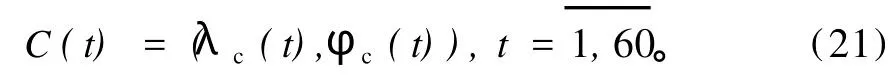
相应地,文献[2,16]用高纬计算方案求得的南亚高压、蒙古高压中心位置指数记为

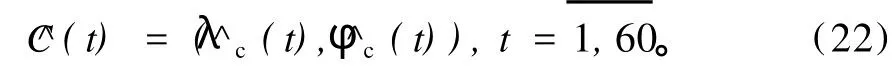
则t年两方案计算结果之差(高纬方案减低纬方案)为

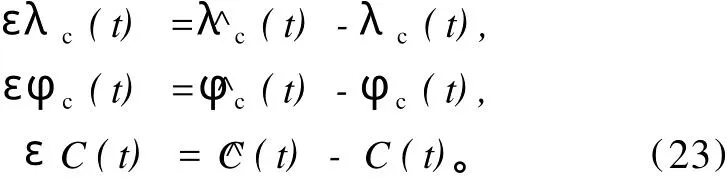
其中,εC(t)是^C(t)、C(t)间在球面上的距离,

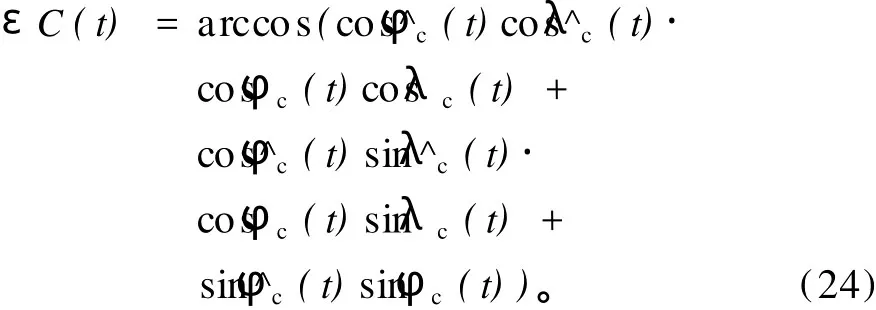
上述统计量(λc、φc、ε λc、ε φc、εC)的60a平均值(以上标“-”表示)、60a绝对平均值(以“”表示用于度量两种方案计算同一系统中心位置的差异。

3.1 南亚高压

由表1可知,两方案求得7月100hPa南亚高压中心位置指数60a平均存在明显差异。达2.63°(它相当于中心偏差292km);它主要由纬向差异ε λc(t)引起达3.05°)。因为7月100hPa南亚高压λc(t)、φc(t)的极差Δ λc、Δ φc分别为18.7°、6.7°,相对偏差近似为1/6、1/10,故用高纬计算方案求出的南压高压中心位置指数(λc(t),φc(t))只是中心位置的近似(图3)。

表1 两种方案7月100 hPa南亚高压(λc,φc)的比较(1948—2007年)Table1 Comparisons of(λc,φc)by the two schemes for100hPa South Asia High in July from1948to2007

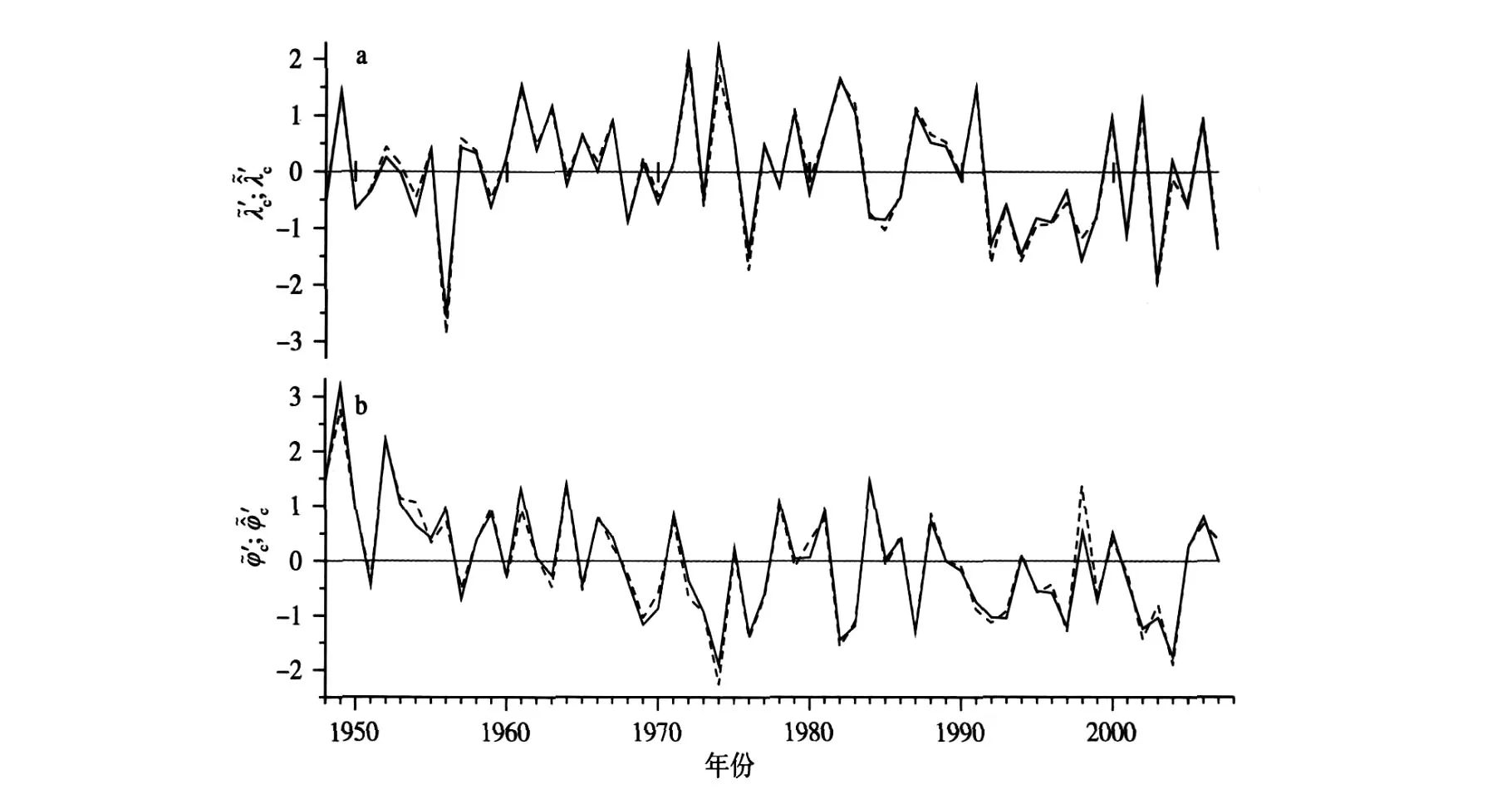
图3 两种方案1948—2007年7月南亚高压中心位置指数标准化序列比较(实线为低纬计算方案,虚线为高纬计算方案) Fig.3 Standardized center local index of South Asia High in July of1948—2007by the two calculation schemes(The solid line is low latitude scheme,and the dash line is high latitude one)

3.2 蒙古高压

由表2可知,两方案求得之1月蒙古高压中心位置指数60a平均相同,精度为0.1°。给出了个别年份月平均图上两方案中心位置偏差(总是正值)的多年平均,其值为0.14°(它相当于15km的偏差);由知,εC(t)主要由ε λc(t)引起。因为1月1 000hPa蒙古高压λc(t)、φc(t)的极差(极大值减极小值)Δ λc、Δ φc分别为12.3°、12.8°,两方案的相对偏差在1%左右,可以忽略不计。因此,低纬系统(λc,φc)计算方案适于高纬系统。

验证表明,低纬气压系统(λc,φc)计算方案既适合于低纬气压系统(λc,φc)的计算,也适合于高纬气压系统(λc,φc)的计算,是求气压系统(λc,φc)普适计算方案。

4 结论

综上,本文分析了文献[10]定义的闭合气压系统中心位置指数(λc,φc)计算方案在低纬气压系统计算中存在的误差,通过建立一组原点位于搜索区Ω中心的新的球面坐标系,实现了低纬闭合气压系统中心位置指数(λc,φc)的准确计算。对7月南亚高压和1月蒙古高压中心位置指数(λc,φc)的实际计算表明,它既消除了低纬系统(南亚高压)

(λc,φc)原计算方案的明显误差,又保持了与高纬系统(蒙古高压)(λc,φc)原计算方案计算结果的一致。因此,本文给出了适于计算任意纬度闭合气压系统中心位置指数(λc,φc)的计算方案。

致谢:本文使用资料由国家自然科学基金委地球科学部南京大气资料服务中心提供,谨致谢忱!

表2 两种方案1月1 000 hPa蒙古高压(λc,φc)的比较(1949—2008年)Table2 Comparisons of(λc,φc)by the two Schemes for1 000hPa M ongolian H igh in January from1949to2008

[1] 《大气科学辞典》编委会.大气科学辞典[M].北京:气象出版社,1994:93.

[2] 陈延聪,王盘兴,周国华,等.夏季南亚高压的一组环流指数及其初步分析[J].大气科学学报,2009,32(6):101-107.

[3] 孙晓娟,王盘兴,智海,等.蒙古高压若干环流指数及与我国冬温异常相关的分析和比较[J].高原气象,待发表.

[4] 施能,朱乾根.南半球澳大利亚、马斯克林高压气候特征及其对我国东部夏季降水的影响[J].气象科学,1995,15(2):20-27.

[5] 崔锦,杨修群.马斯克林高压的变化及其与ENSO的关系[J].气象科学,2005,25(5):441-449.

[6] 顾思南,杨修群.北半球绕极涡的变异及其与我国气候异常的关系[J].气象科学,2006,26(2):135-142.

[7] 朱乾根,施能,吴朝珲,等.近百年北半球冬季大气活动中心的长期变化及其与中国气候[J].气象学报,1997,55(6):750-758.

[8] 龚道溢,王绍武.西伯利亚高压的长期变化及全球变暖可能影响的研究[J].地理学报,1999,54(2):125-133.

[9] 侯亚红,杨修群,李刚.冬季西伯利亚高压变化特征及其与中国气温的关系[J].气象科技,2007,35(5):646-650.

[10] 王盘兴,卢楚翰,管兆勇,等.闭合气压系统环流指数的定义及计算[J].南京气象学院学报,2007,30(6):730-735.

[11] 数学手册编写组.数学手册[M].北京:高等教育出版社,2005:52.

[12] 管树轩,王盘兴,麻巨慧,等.北半球10hPa极地涡旋环流指数定义及分析[J].高原气象,2009,28(4):777-785.

[13] 麻巨慧,王盘兴,郭栋,等.南半球10hPa极地涡旋环流的多尺度变化特征分析[J].高原气象,2009,28(6):1299-1307.

[14] Li Liping,Guan Shuxuan,Wang Panxing,et al.Definition and analysis of the circulation indices of polar vortex at 10hPa in the Northern Hemisphere[J].Sciences in Cold and A rid Regions,2009,1(6):549-558.

[15] Li Liping,Ma Juhui,Wang Panxing,et al.Multi-scale variation characteristics of polar vortex at10hPa in the Southern Hemisphere[J].Sciences in Cold and A rid Regions,2010,2(1):73-81.

[16] 刘晴晴,王盘兴,徐祥德,等.蒙古高压一组环流指数与我国同期气侯异常关系分析[J].热带气象学报,待发表.

[17] 麻巨慧,王盘兴,李丽平,等.“0801南方雪灾”与同期蒙古高压中期活动关系的分析[J].大气科学学报,2009,32(5):652-660.

[18] W ang Panxing,W ang Julian X L,W ang Yukun,et al.Circulation indices of the Aleutian low pressure system and its definitions and relationships to N.H.climate anomalies[J].GRL,审稿中

[19] Kalnay E,Kanamitsu M,Kistler R,et al.The NCEP/NCAR40-year reanalysis project[J].Bull Amer Meteor Soc,1996,77(3):437-471.

[20] Simmons A J,Gibswson J K.The ERA-40project Plan[M]//ECMW F.ERA-40projects report series.Shinfield Park,Reading:ECMW F,2000:1-62.

Calculation Method of Center Position Index for Closed Pressure Systems

WANG Pan-xing,ZHAO Hui,REN Lü,LUO Xuan,GUO Dong

(School of Atmospheric Sciences,NU IST,Nanjing 210044,China)

Areaindex S,strength index P and center longitude/latitude position index(λc,φc)have been defined in the paper Definition and calculation of three circulation indices for closed pressure systems written by Panxing Wang,et al.But the calculated index(λc,φc)for the lower latitude system s exist obvious errors,which is induced by the unsuitable polar spherical coordinate.Thus,a new spherical coordinate with the original point locating in the center of searching area is established,in such a way that the(λc,φc)is accurately calculated.The practical calculations of(λc,φc)for South Asian High in July and Mongolian High in January show that the evident errors are eliminated and the calculated results are in accordance with the original one.Therefore,this method can be applied to random closed pressure system s.

closed pressure system;center location index;calculation scheme

P434

A

1674-7097(2010)05-0520-07

2010-02-06;改回日期:2010-09-10

国家自然科学基金资助项目(40633018);江苏省研究生培养创新工程创新计划项目(CX08B_016Z)

王盘兴(1943—),男,江苏常州人,教授,博士生导师,研究方向为大气环流异常、短期气候预测,wangpx@nuist.edu.cn.

王盘兴,赵辉,任律,等.闭合气压系统中心位置指数的计算方案[J].大气科学学报,2010,33(5):520-526.Wang Pan-xing,Zhao Hui,Ren Lü,et al.Calculation method of centerposition index for closed pressure systems[J].Trans Atmos Sci,2010,33(5):520-526.

(责任编辑:倪东鸿)