线性化二粒子Boltzmann方程组的特征值问题

布仁满都拉，赵迎春

（1.赤峰学院 数学学院；2.赤峰学院 初等教育学院，内蒙古 赤峰 024000）

线性化二粒子Boltzmann方程组的特征值问题

布仁满都拉1，赵迎春2

（1.赤峰学院 数学学院；2.赤峰学院 初等教育学院，内蒙古 赤峰 024000）

首先推出了二粒子～Boltzmann方程组的线性化方程组，其次利用线性化Boltzmann方程组的积分算子的特征值，特征函数求出了线性化二粒子～Boltzmann方程组积分算子的特征值，特征函数.

线性化二粒子～Boltzmann方程组；特征值；特征函数

1 预备知识

称g,h为二点相关函数和三点相关函数，表示分子偏离分子混乱的程度.对于稳定的层流，这些项可以忽略，但对于非稳定流这些项将十分重要.在本文中我们将三点混乱水平上讨论问题，即假定h=0,此时Boltzmann方程系[5,6]的最初两个方程可以独立求解.写出这两个方程如下（称为二粒子Boltzman方程组）：

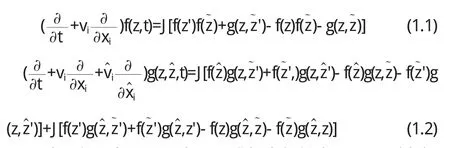
以上方程中z-(x,V)表示六维相空间的点，x,V分别为粒子的的位置和速度，带撇的变量表示分子碰撞后的值.J表示碰撞积分算子：

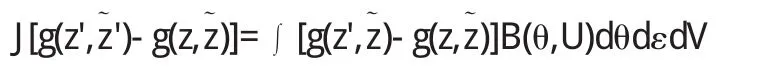
将(1.3)代入(1.1),(1.2),经过简化得

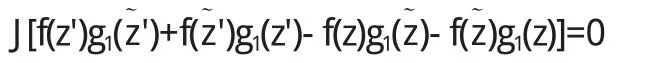
这说明了f(0),g1(0)是(1.4),(1.5)的局部平衡解，进一步可知，f(0)(z,t),f(0)(z,t)f(0)(z,t)是(1.1),(1.2)的局部平衡解.

2 线性化二粒子～Boltzmann 方程组的积分算子的特征值，特征函数

假设

且f和g与位置x无关,f(0)的参数与时间和位置无关.将(2.1)代入(1.4)和(1.5)并且忽略二阶无穷小量，得

称(2.2)，(2.3)为线性化的二粒子Boltzmann方程组.

下面我们研究特征值问题

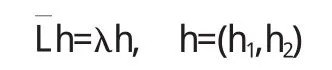
这里我们允许h1,h2是广义函数[4],否则当λ≠0时可能没有非零解.

(2.5)+(2.6)，(2.5)-(2.6)得：

若 λ=0,则当 h,φ 取相同的碰撞不变量(ψ=a+b.V+cv2.其中a,c是常数，b是常矢量)时,(2.5),(2.6)成立.由(2.7)可得 λ=0是L的特征值，h+φ是对应的特征函数.若λ≠0，则由（2.7）可知 h=φ.关系式（2.7）知是L的特征值，h+φ是对应的特征函数.

2.设λ是L的特征值，h是与λ对应的特征函，则

这里 h=φ.(2.8),(2.9)说明了 2 λ 是L軈的特征值，(h,h)是与 λ对应的特征函数.

由 1,2可知{L軈的全部特征值}={2 λ|λ 是 L的特征值}.根据上面的讨论可知,由L的特征值和特征函数能得出L軈的特征值和特征函数.因此只讨论L的特征值和特征函数即可.

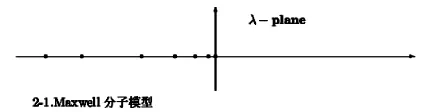
(1)设气体分子是Maxwell's分子.

由于L的特征值和特征函数[4]为

其中 Ylm(θ,φ)是球谐函数，Lnα(z)是连带的拉盖尔多项式[4].因此的特征值}={2 λnl|λnl是 L的特征值}，与λ軈nl对应的特征函数为(gnlj,gnlj)

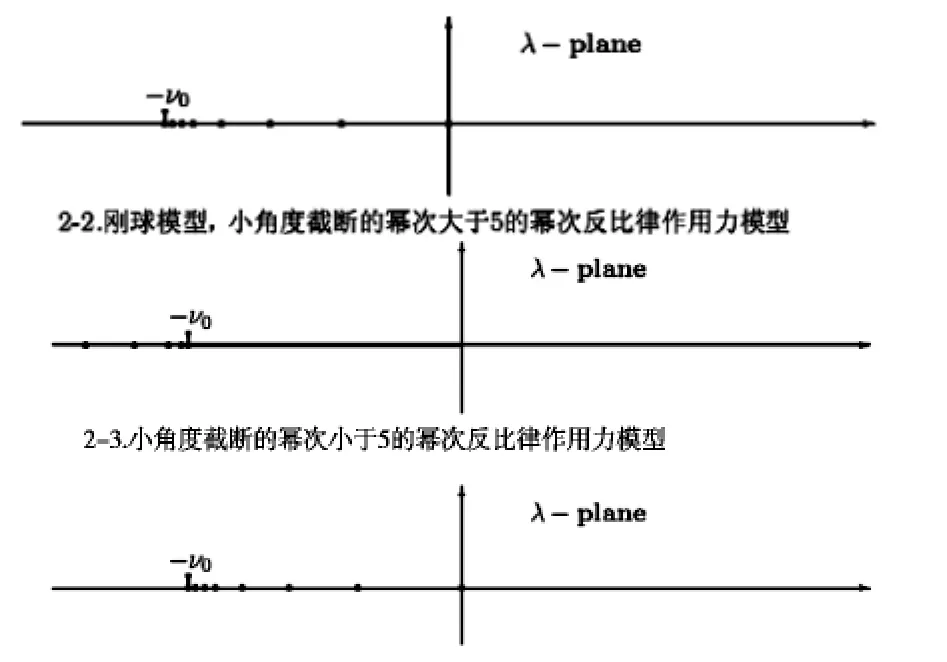
(2)由[2],[4]可知，对刚球模型，小角度截断的幂次大于5的幂次反比律作用力模型，小角度截断的Max well分子模型,有Lh=Kh-v(c)h.

其中K是积分算子，且紧算子[2],[4],[10],v(c)是乘法算子.对刚球模型，小角度截断的幂次大于5的幂次反比律作用力模型,当c从零到正无穷时v(c)从最小值v(0)单调增加到正无穷.对小角度截断的幂次小于5的幂次反比律作用力模型，当c从零到真无穷时v(c)从vi(0)单调递减到零.对小角度截断的Max well分子模型，v(c)是常数.在[2],[4]中，利用Weyl定理证明了λ=-v(c)是Li的连续谱.还已知L存在无穷多个离散的特征值[4]，集中于v(0).对刚球模型，小角度截断的幂次大于5的幂次反比律作用力模型，L的离散的特征值位于区间(-v(0),0]内.对小角度截断的幂次小于5的幂次反比律作用力模型，L的离散的特征值位于(-∞,-v(0)).对小角度截断的Max well分子模型，L的离散的特征值位于[-v(0),0].所以有如下谱分布:

设v0=2 v(0)

〔1〕S.chapman and T.G.Cowling.The MathematicalTheory of the Non-Uniformgases,Cambridge Univercity Press(1953).

〔2〕H.Grad,Asymptotic Theory of the Boltzmann Equation,ll.Phys.Fluid,6:147-181,1963.

〔3〕H.Grad,Principles of the Kinetic theory of Gases,in Handbuch der Physik,vol.12.S.Flugg-e.Ed.(Springer-Ver lag,Berlin,1958)pp.205-294.

〔4〕C.Cercignani,The Boltzmann Equation and Applications,Scottish Academic Press,Edinburgh(1975).

〔5〕陈建宁～$Boltzmann$方程的两个解的平均作为二粒子～$Boltzmann$方程系的解.数学物理学报，1990（3）：259-272.

〔6〕Tian-quan Chen,Hilbert-Enskog-Chapman Expansion in the Turbulent Kinetic Theory of Gases,l,Journal of statisticalphysics,Vol 25,No,3,1981.

〔7〕K.Sagara,S.Tsug$acute{e}$,A bimodal Maxwellian distribution as the equilibrium solution of the two-particle regime,Phys.Fluids,vol.25,No.11,November 1982.

〔8〕S.Tsug$acute{e}$,Apporoach to the origin of turbulence on the basis of two-point kinetic theory,Phys.Fluids,vol.17,No.1,November 1974.

〔9〕S.Tsug$acute{e}$,K.Sagara,Kinetic theory of turbulent compressible flows and comparison with classical theory,Phys.Fluids,vol.19,No.10,November 1976.

〔10〕Robert T.Glassey,The Cauchy Problem IN Kinetic Theory,Publisher:Society for Industrial Mathematics,1987.

O 175.3

A

1673-260X（2010）12-0023-02