橡胶止水带受力状态下的有限元分析
2010-10-17陈尔凡
陈尔凡, 陈 珂, 马 驰, 信 莹
(沈阳化工学院,辽宁省高校“高分子材料应用技术”重点实验室,辽宁 沈阳110142)
橡胶止水带受力状态下的有限元分析
陈尔凡, 陈 珂, 马 驰, 信 莹
(沈阳化工学院,辽宁省高校“高分子材料应用技术”重点实验室,辽宁 沈阳110142)
应用大型有限元分析软件ANSYS,建立了橡胶止水带于混凝土中在不同受力形式下的有限元模型,分析了在各种不同工况下止水带变形及应力的分布,描述了其可能出现裂纹的位置。通过分析计算得出,当止水带在混凝土中受力而产生应力时,对止水带伸缩性起主要作用的是中心孔的横梁结构,此部位承受了较大的应力。与此同时,计算得出在各种工况下止水带所受最大应力以及止水带中心孔横梁结构中心节点的最大反力。分析了各种工况下最大应力与位移的关系,以及止水带中心孔横梁结构中心节点反力与位移的关系。为止水带的设计、生产、安装及模型优化提供了依据。
橡胶止水带;有限元;受力分析;ANSYS
橡胶止水带广泛应用于基本建设、地下设施、隧道、水利、地铁等工程,为闸门、坝底、建筑工程、地下建筑物等伸缩缝混凝土浇注配用[1]。利用橡胶的高弹性和压缩变形性,止水带在各种载荷下产生弹性变形,从而起到紧固密封的作用,有效地防止建筑构件漏水、渗水,并起到减震缓冲作用,从而确保工程建筑物的使用寿命。1959年北京火车站地下通道内首次应用了橡胶止水带。我国生产使用橡胶止水带已有40多年的历史。但是,在日常工程使用中止水带断裂失效行为较为常见,在工程、安装和设计中均很难预防[2,3]。
本文主要利用有限元软件对三元乙丙橡胶止水带进行建模和计算,从中可以清晰地看出止水带在不同工况下的变形情况以及应力分布,对研究止水带的老化失效提供了直观的依据,对止水带的设计、安装以及模型优化提供了依据。
1 建立模型
1.1 几何模型的建立
在对止水带进行有限元分析时,将其在混凝土中嵌入时的状况看作是无限延伸的平面。所以,可将它的受力模型简化为平面模型。又由于考虑到止水带嵌入到混凝土中的部分已经连同混凝土一起固化,所以,整体模型忽略了接触分析。建立后的几何模型如图1所示。

图1 橡胶止水带几何模型
1.2 有限元模型的建立
1.2.1 橡胶材料的模型
橡胶材料属于高弹性近似不可压缩体。其本构关系是复杂的非线性函数,通常用应变能密度函数表示,在受力后呈现大应变和大位移。力学模型表现为复杂的材料非线性和几何非线性,其变形后的体积可近似地看作不变。目前,广泛采用Mooney-Rivlin模型描述橡胶材料的应变能函数[4]。根据橡胶的应力-应变关系采用二项式的Mooney-Rivlin函数,其函数表达式(1)可表示为:
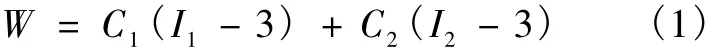
式中,W为应变能密度;C1、C2为材料 Mooney-Rivlin系数;I1、I2为第一、第二应变张量不变量。
1.2.2 参数的选取
三元乙丙橡胶材料的弹性模量E=7.8 MPa,泊松比 υ =0.499[5]。试样经混炼、硫化、拉伸等实验后计算得出应力-应变曲线(见图2)。经拟合应力-应变曲线得出应变能函数[6]的参数 C1=4.960 3E+005,C2=2.689 1E+007。所选用的混凝土强度标号为C40,弹性模量E=32 500 MPa,泊松比υ=0.167。橡胶和混凝土分别选取的单元类型为ANSYS中8节点的plane183单元和4节点的plane42单元。

图2 应力-应变曲线
1.2.3 网格划分
混凝土的网格划分为0.005 m,止水带的网格划分为0.001 m,其长度仅为止水带最小边的1/4。网格划分完成后的模型如图3所示。

图3 网格划分
2 计算结果及讨论
2.1 工况设计
按 ANSYS 工况设计原则[7,8],在常温状态下止水带在大坝中频繁发生的变形工况有三种,即:
(1)止水带两侧混凝土块同时沿与X轴向相反的方向分别拉伸移动10 mm(设定),此过程在Y方向上无位移。经ANSYS求解计算,所得变形及应力如图4所示。
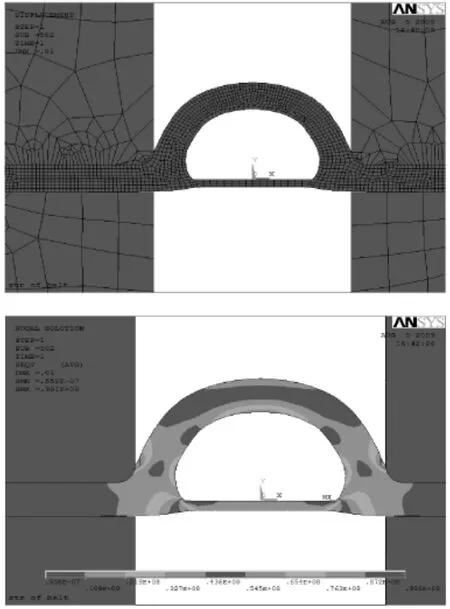
图4 止水带受拉伸力作用时的变形及应力图
(2)止水带两侧混凝土块同时沿与X轴向相对的方向分别压缩移动5 mm(设定),此过程Y方向上无位移。经ANSYS求解计算,所得变形及应力如图5所示。

图5 止水带受压缩力作用时的变形及应力图
(3)止水带两侧混凝土块同时沿与Y轴向相对的方向分别错位移动10 mm(设定),此过程X方向上无位移。经ANSYS求解计算,所得变形及应力如图6所示。
2.2 计算结果
从图4可知,在施加拉伸力并位移后止水带的中心孔左右分别变形了0.01 m,应力最小处在混凝土中的止水带中心孔顶部,最大应力出现在止水带中心孔的横梁结构上。
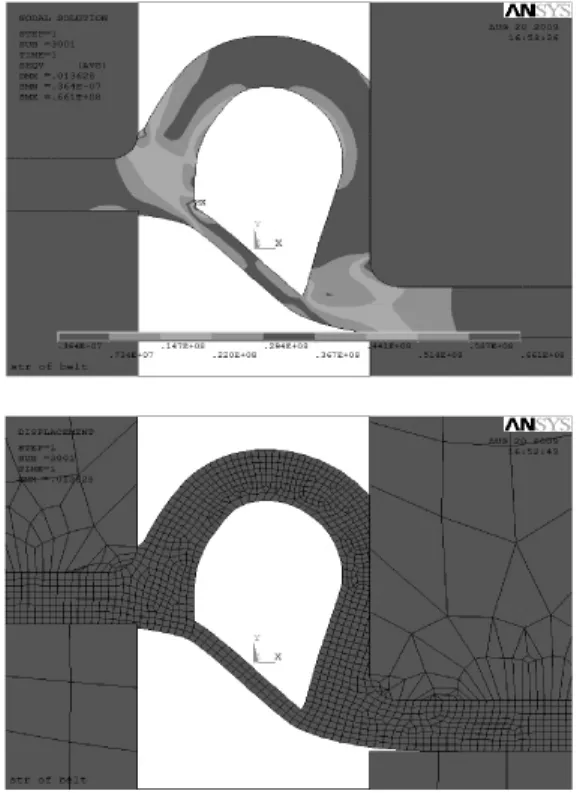
图6 止水带受剪切力作用时的变形及应力图
由图5可知,在对混凝土中的止水带施加压缩力并位移后,止水带的中心孔左右分别变形了0.005 002 4 m,应力最小是混凝土中止水带中心孔的顶部,最大应力出现在止水带中心孔横梁结构的中部。
由图6可知,在对混凝土中止水带施加剪切力并位移后,止水带的中心孔左右分别变形了0.013 628 m;应力最小处是混凝土中止水带中心孔的顶部,最大应力出现在止水带中心孔横梁与内孔交接的端点。各种工况下的最大应力及最小应力数值如表1所示。

表1 各种工况下的最大应力及最小应力数值
2.3 结果分析
从以上所得到的变形图及应力图可以看出,对止水带在混凝土中受力起决定性作用的是中心孔的横梁结构。从上述图中还可以看出,Von Mises应力[9,10]在横梁结构上的分布是比较集中的。Von Mises应力反应了截面上各主应力差值的大小,一般来说,Von Mises应力越大,将加速橡胶材料的松弛,造成刚度下降,材料越容易出现裂纹,所以,止水带中心孔的横梁结构既是承受应力的部位,也是最先开始损坏的部位。
2.3.1 各工况下最大应力与位移的关系
根据计算结果可知,止水带中心孔的横梁结构是止水带在混凝土中受力的主要部位,在混凝土中受力时起缓冲伸缩的作用。在止水带发生位移时,最大应力一直保持在横梁结构上。各种工况下最大应力与位移的关系如图7所示。

图7 各种工况下最大应力与位移的关系曲线图
由图7看出,止水带在受到拉伸力与剪切力作用位移后,最大应力与位移呈现明显的非线性关系,而止水带在受到压缩位移时,最大应力与位移几乎接近线性关系。这是由于止水带的横梁结构很薄,所以,当受到压缩时,力主要被传递到横梁结构上,最大应力与位移的关系曲线自然会接近线性的关系。当受到拉伸力和剪切力作用并位移时,受力开始时止水带中心孔的顶部与横梁都同时承受了力,因而应力起初比较分散,最大应力初始时并不随位移增大而呈线性递增。但受力到中期以后,主要受力部位为横梁结构,此时,应力都集中到此部位,最大应力开始明显增大。
2.3.2 中心节点反力与位移的关系
将所选取的止水带中心孔横梁结构的中心点作为节点,根据计算结果得出中心孔反力与位移的关系曲线,见图8所示。各种工况下止水带中心孔横梁结构中心点最大反力如表2所示。

表2 中心孔横梁结构中心点最大反力数值

图8 中心孔横梁结构中心点反力-位移关系曲线
从所选节点的计算结果可知,当受到剪切力和拉伸力作用并位移时,中心孔横梁结构中心点的反力曲线是先呈上升趋势,而后经过一个拐点后再平稳上升。而受到压缩力作用并位移时,反力曲线则一直呈稳步递增趋势,这与最大应力与位移的关系曲线是相符的。
3 结论
通过对橡胶止水带在各种工况下进行的非线性有限元分析,得出结论如下。
(1)止水带受到混凝土的拉伸力而变形了0.01 m时,最大应力出现在止水带中心孔的横梁结构上(0.981E+08Pa)。受到混凝土的压缩力而变形了0.050 024 m时,最大应力出现在止水带中心孔横梁结构的中部(0.827E+07Pa)。受到混凝土的剪切力作用而变形了0.013 628 m时,最大应力出现在止水带中心孔横梁与内孔交接的端点(0.661E+08Pa)。中心孔的横梁部分是伸缩缝中起缓冲作用的主要结构,横梁部分承受了较大的应力,是受到外力作用时主要的受力部分。
(2)根据各种工况下最大应力与位移的关系曲线以及所选中心孔横梁结构中心节点的反力与位移的关系曲线,可以观察到最大应力随位移改变时的发展趋势,可以更直观地看到力与位移的关系。
(3)通过有限元分析,得出橡胶止水带在各种工况下的变形及应力分布、受力部位以及可能出现裂纹的位置。在大应力和大变形时,横梁可被拉断,其变形远大于材料本身的变形。可满足大变形的需要,能起到很好的止水作用,为其合理设计、生产、安装及模型优化提供了理论依据。
[1] 刘杰胜,吴少鹏,陈美祝.伸缩缝止水材料的性能及应用[J].水科学与工程技术.2008,(4):6-8.
[2] 沈春林.国内外防水材料的现状与发展概况[J].工业建筑.2004,30(6):1-4.
[3] 徐启洪.橡胶止水带的现状和发展[J].中国橡胶.2002,1(10):22-25.
[4] 张振秀,聂 军,沈 梅,辛振祥.ANSYS中超弹性模型及其在橡胶工程中的应用[J].橡塑技术与装备.2005,31(9):1-5.
[5] 吴绍吟译.橡胶的本体模量和泊松比[J].世界橡胶工业.1987,(4):3-17.
[6] 王 伟,邓 涛,赵树高.橡胶 Mooney-Rivlin模型中材料常数的确定[J].特种橡胶制品.2004,25(4):8-10.
[7] John F.Hunt,P.E.3D Engineered Fiberboard:Finite Element Analysis of a New Building Product[C].International ANSYS Conference.Pittsburg,PA,May 24-26,2004.
[8] 郝文化.ANSYS实例分析及应用[M].北京:清华出版社,2004,177-212.
[9] Gent A N.Engineer with Rubber-How to Design Rubber Components[M].New York: Hanser Gardner Publications,2001.259-275.
[10] Gao Y C,Gao T S.A Rubber Wedge Under the Compression of a line load[J].Int..J.Solids and Structures.1994,17: 2393-2406.
[责任编辑:张启跃]
Abstract:By utilizing finite element analysis software ANSYS,a finite element model of the rubber water-stop in concrete by different force conditions was set up.The deformation and stress distribution under several different load conditions were analyzed.Then the position of possible crack was described.The analysis shows that when the water-stop in the concrete was force to generate stress,the crossbeam of central hole played a major role and bear a larger stress.And the maximum stress in a variety of load conditions and the maximum inversed force of crossbeam of central hole were obtained.Then in a variety of load conditions,the relationship between the maximum stress and disaplacement,as well as the relationship between the maximum inversed force and disaplacement were analyzed.The analysis results provide the basis for the design,production,installation and optimization of model for the water-stop.
Keywords:Rubber water-stop;Finite element;force analysis;ANSYS
Finite element analysis of rubber water-stop beared forces
CHEN Er-fan, CHEN Ke, MA Chi, XIN Ying
(Key Laboratory of Applied Technology of Polymer Materials,Shenyang Institute of Chemical Technology,Shenyang 110142,China)
TQ 336.5
B
1671-8232(2010)11-0015-05
2009-11-20
辽宁省教育厅资助(No.2007T145、2007T154),沈阳市科技基金(No.091444)。
陈尔凡(1955-),男,博士,博士生导师,教授,主要从事高分子复合材料研究。发表论文120余篇,近年来获省部级科技进步奖九项。
