基于主成份分析和支持向量机的PCA-SVM储层识别模型研究
2010-10-17张哨楠匡建超
王 众,张哨楠,匡建超,罗 鑫
(1.油气藏地质及开发工程国家重点实验室 成都理工大学,四川成都 610059;2.成都理工大学能源学院,四川成都 610059)
基于主成份分析和支持向量机的PCA-SVM储层识别模型研究
王 众1,2,张哨楠1,2,匡建超2,罗 鑫2
(1.油气藏地质及开发工程国家重点实验室 成都理工大学,四川成都 610059;2.成都理工大学能源学院,四川成都 610059)
储层识别是油气勘探开发中所面临的关键问题和难点之一。针对传统储层识别方法预测精度较低这一问题,提出了基于主成份分析和支持向量机的PCA-SVM储层识别模型,较好地解决了传统学习方法在非线性预测中的小样本、过学习、局部极小点等问题,同时消除了出入变量之间的多重相关性,减少了输入变量的个数,提高了预测精度和收敛速度。通过对长庆中部气田马五1段储层的实例应用,PCA-SVM模型的预测精度达到100%,优于SVM模型(93.6%)和Fisher判别模型(96.3%)。这表明PCA-SVM模型具有更高的预测精度,为致密储层的准确识别探索了又一新方法。
主成份分析;支持向量机;PCA-SVM模型;储层识别
0 前言
储层识别一直都是油气勘探与开发领域的一项基本任务,其结果的正确性直接影响到油气田的开发效果[1]。前人对此进行了大量研究,提出了逐步回归[2]、动态聚类[3]、模糊识别[4]、逐步判别[5]等方法,并取得了一定成效。但由于储层识别属于非线性预测问题,加之绝大部份油气田地质条件复杂,所以上述模型对于致密储层的识别受到多方面的限制,导致预测精度不高。针对上述问题,有学者提出了利用神经网络来进行致密储层识别,并在实践中取得不错效果[6、7]。然而,普通神经网络存在收敛速度慢,易陷入局部最优解等问题[8];此外,由于影响储层的因素多而复杂,使得传统储层识别方法在实际应用过程中常遇到以下问题:①输入参数过多,彼此相互关联,导致信息重叠与数据冗余,影响模型的预测精度与计算速度;②输入参数过少,难以全面准确反映与刻画储层的全貌,导致预测精度降低[1,6]。
支持向量机(Suppo rtVecto rM achine,SVM)是近来广泛应用的一种新型机器学习方法,以结构风险最小化原则代替神经网络的经验最小化原则,被认为是目前针对小样本非线性分类和预测等问题的最佳理论[9]。基于此,作者将与SVM与主成份分析相集成,提出了PCA-SVM储层识别模型。该模型不仅较好地解决了神经网络固有的过学习以及局部极小点等问题,而且消除了输入变量间的多重相关性,提高了储层识别的精度。
1 PCA-SVM模型构建
1.1 主成份分析基本原理[10]
主成份分析法(Princip le ComponentAnalysis,PCA)是目前广泛应用的一种降维技术。设X=(x1,x2,…,xp)T是P维随机向量(E X=u,D X=V≥0),PCA的基本思想就是将这p个特征变量x1、x2、…、xp综合成尽可能少的几个综合变量y1、y2、…、yq(q≤p),且要求y1、y2、…、yq既能充分反映x1、x2、…、xp所携带的信息,又能使得这个q个新变量互不相关。由于y1要反映原来变量所携带的信息,则y1应是x1、x2、…、xp的线性组合,即
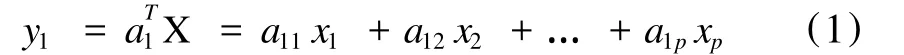
其中 a1=(a11,a12,…,a1p)T为非零常向量。
要使y1能最大限度地反映原来p个特征变量所携带的信息,就要使得y1的方差(式2)尽可能地大。
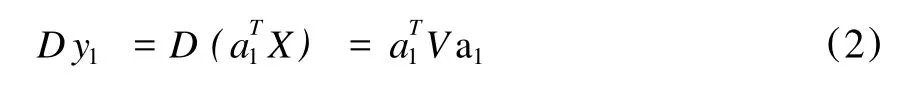
由于不能通过增大向量a1的长度来使D y1变大,那么求解y1的问题就归结为在a1满足单位化条件a1Ta1=1之下,求使得D y1达到最大的a1。通过lagrange乘数法可以求解此问题,具体推导过程请参见文献[10],最终可以得出公式(3)。
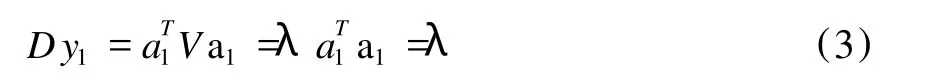
其中 λ是协方差阵V的特征根。
使得D y1最大即是让λ的值最大。设λ1是协方差阵V的最大特征根,则a1就是λ1所对应的单位化特征向量,这样就求出了第一个综合变量y1。同理可以求出y1、y2、…、yq,并称y1、y2、…、yq为第一、第二、……、第p个主成份。
1.2 支持向量机基本原理[11]
支持向量机(SVM)是Vap ink等人在二十世纪九十年代,基于统计学习理论和结构风险最小化原则提出的一种新型学习机器[12]。SVM解决了传统学习方法中“维数灾难”问题,具有对样本依赖小,解为全局最优解及泛化能力强等优点,已被广泛应用于模式识别和预测等领域,成为既神经网络之后机器学习领域的研究热点[13]。
利用SVM进行分类预测的基本思想,就是通过非线性变换,将输入变量x转化到某个高维空间中,然后在变换空间中求解最优分类面,获得决策函数。目前,C-支持向量分类机(非线性软间隔分类机)在实际应用中分类效果较好,是一种经常使用的支持向量分类机。其算法如下:
设样本集T={(x1,y1),…,(xl,yl)}∈(X×Y)l,且xi∈X=Rn,yi∈Y={1,-1},i=1,…,l。定义核函数:
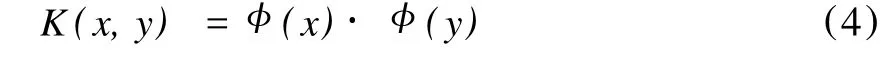
首先,通过非线性映射 φ:Rn→H将输入变量映射到高维H ilbert空间H中。此时,“最大间隔”非线性支持向量机的目标函数可表示为式(5)。

相应的分类函数可表示为:
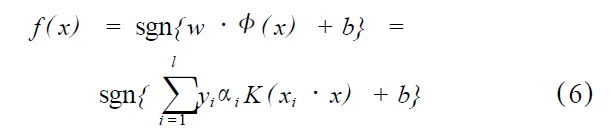
则C-SVM就转化为在选择K(x,x′)和适当的参数C的基础上,求解下面最优化问题:
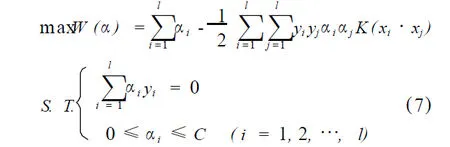
对于不同的核函数,可以产生不同的支持向量机。常用的核函数有以下三种:
(1)多项式核:
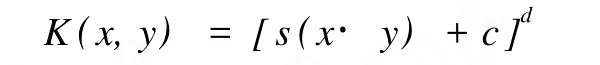
(2)径向基函数(RBF)核:
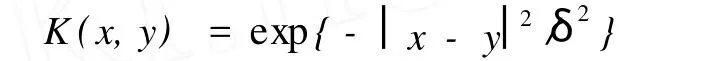
(3)二层神经网络:

1.3 PCA-SVM储层识别模型原理
由于影响储层分类的因素多且还存在相关性,所以SVM在实际应用过程中同样会遇到:①输入参数过多导致信息相互重叠,影响模型精度和收敛速度;②输入参数过少导致难以全面准确反映储层全貌,预测精度降低的问题。基于此,作者汲取主成份分析和支持向量机的优点,提出了PCA-SVM储层识别模型,该模型不仅消除了变量间的多重相关性,同时减少了输入变量个数,提高了收敛速度和识别精度。其模型的建模步骤如下:
(1)制定储层分类标准,对需要预测的油(气)田储层进行分类。通常储层可以分为:工业流油(气)层、含油(气)层、油(气)水同层、干层四类。
(2)选择原始输入变量,建立SVM的训练样本集。
(3)利用PCA对输入的变量进行处理,从中选取最能代表原始信息的主成份。
(4)挑选出的主成份作为C-SVM的输入,对未知储层的类别进行预测,其计算过程为[14]:①选择合适的核函数,在实际应用中一般选用RBF函数;②由于核参数σ和惩罚因子C的选取,直接影响到模型的稳定性和泛化能力的强弱,为防止过拟合,可以运用网格法和交叉验证法来寻找核参数和惩罚因子的最优值C*和σ*;③运用C*和σ*对收集的样本进行训练SVM;④对训练好的SVM进行检验。在通常情况下,当回判率大于90%时,SVM才能用作预测;⑤运用达到精度要求的SVM,对未知储层的类别进行预测。
2 实例应用
长庆中部气田位于鄂尔多斯盆地中部,在榆林、乌审旗、定边和延安之间,面积超过1×104km2,其奥陶系马家沟组岩性复杂,属于致密储层,对该储层的准确识别,是该地层天然气开发中所面临的关键问题。作者以长庆中部气田马五1段储层为例,运用PCA-SVM模型对其储层类别进行预测,并将预测结果同目前常用方法进行了比较。
2.1 储层分类
根据中部气田的实际情况,按照鄂尔多斯盆地的储层分级标准,并结合前人研究成果,作者将马五1段储层分为四类:工业气层(I类)、含气层(II类)、气水同层(III类)和干层(IV类)(见表1)。

表1 中部气田储层分级标准Tab.1 Standard of reservoir classification in central gas-field
2.2 选取模型参数和样本
在对研究区大量参数的分析以及咨询专家的基础上,挑选出八个与储层性质、特征相关的参数,分别是:①电阻率(Rlld);②深浅双侧向电阻率幅度差(△R);③自然伽玛(GR);④测井声波孔隙度(Φs);⑤渗透率(K);⑥储渗因子(KΦs);⑦可动水指数(RR);⑧介质类型因子(EE)。
作者选用了长庆中部气田马五1段19口井分层测试的92个已知样本[15](见表2)。为了检验模型预测分类的有效性,作者随机选取表2中前65个已知样本作为训练数据,后27个样本作为预测数据。
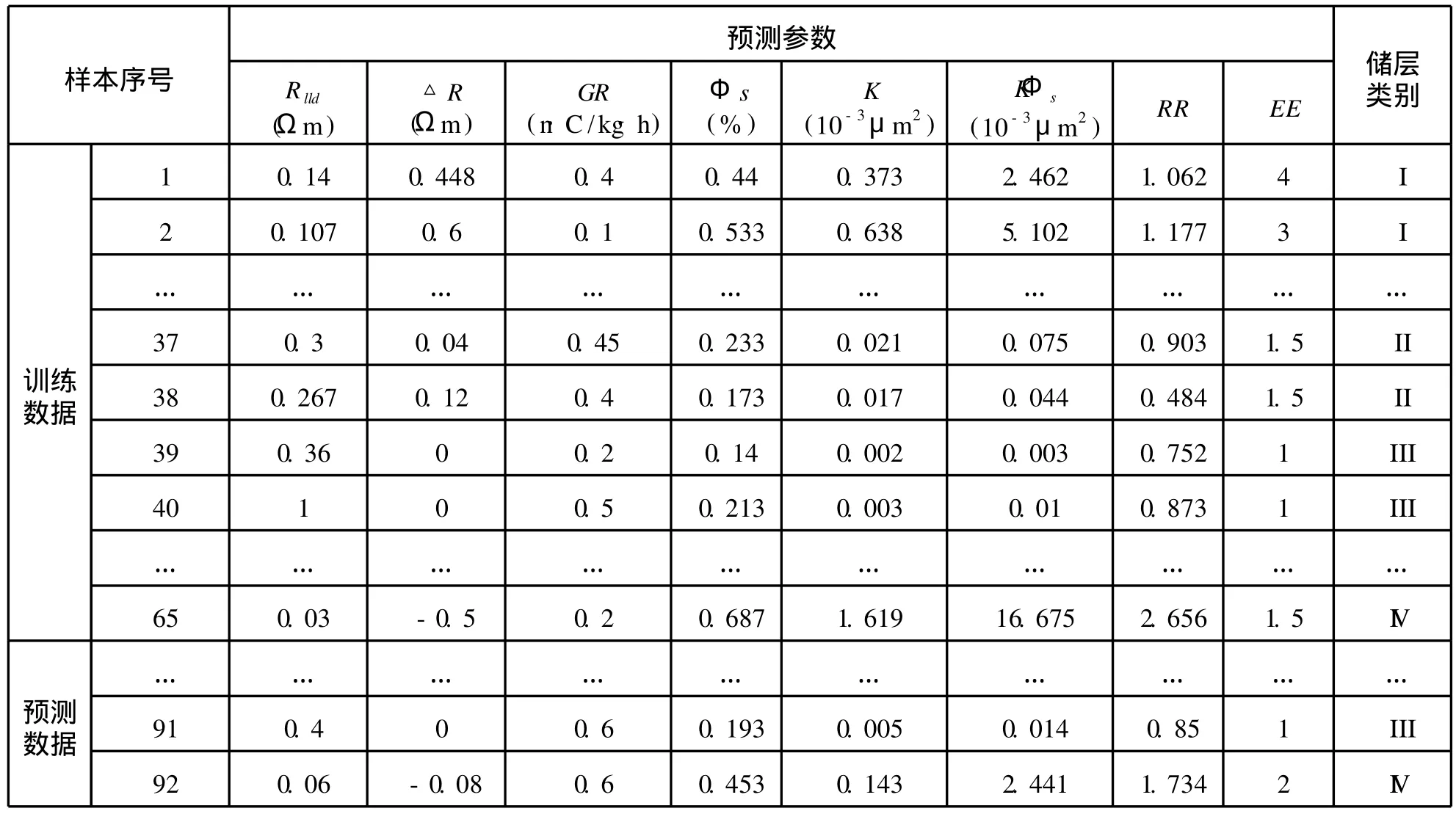
表2 已知样本汇总表Tab.2 Param eterof samp les
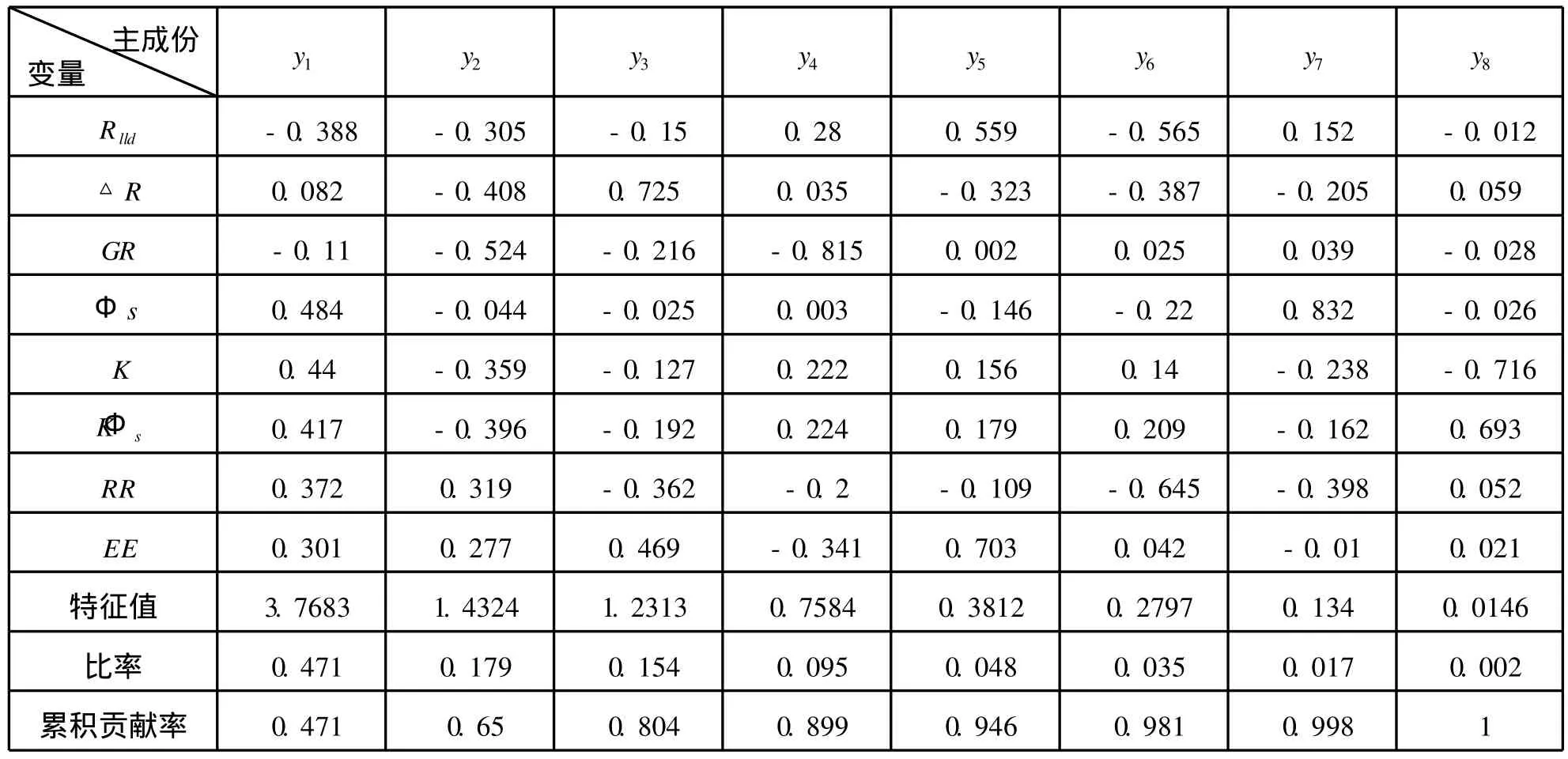
表3 各主成份的载荷系数和贡献率Tab.3 Loading and variance contribution of each p rincip le component
2.3 储层识别
首先根据式(1)~式(3),作者运用M IN ITAB的PCA工具箱对表2中的数据进行处理,求出各主成份的载荷系数和累计贡献率(由于篇幅限制,具体计算过程请参见文献[16])。根据计算结果(见表3),作者选取前代表原始信息94.6%的前5个主成份作为SVM的输入变量。
作者运用libsvm-2.88软件来完成SVM分类预测的实现。首先选取RBF作为核函数,以表2中的前65个作为训练样本,对SVM进行训练(以5个主成份作为输入变量,储层类别为输出变量)。通过多次参数的调整,求得核参数和惩罚因子的最优值C=1 448.154 687 87,σ=0.005 524 271 728 02(见图1),当回判率达到95.38%时(见图2),表明该模型的精度已经达到要求,可以进行预测。最后以表2中余下27个样本作为检验,预测正确率达100%(见下页表4)。
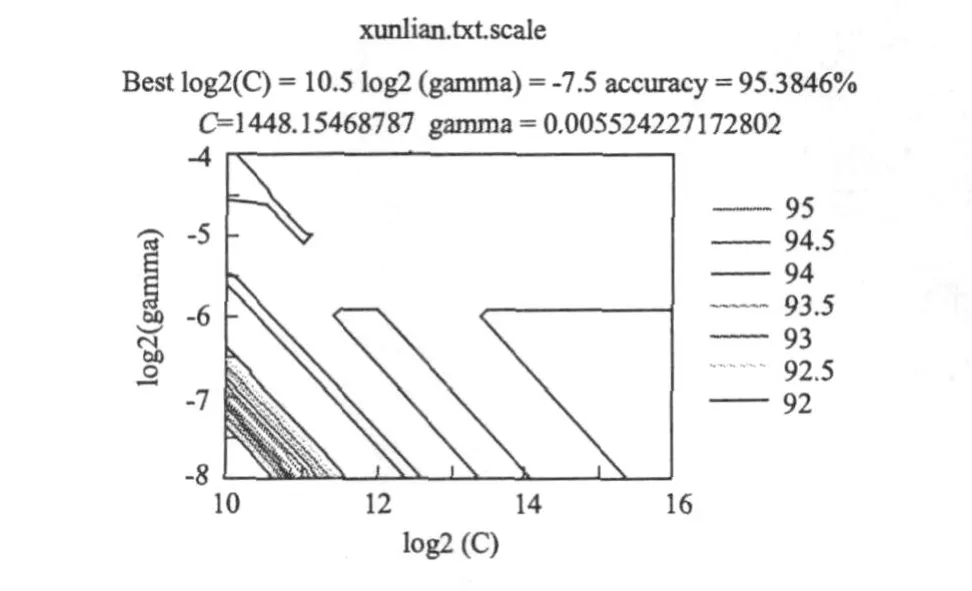
图1 网格搜索C和σ的最优值图Fig.1 Op timal value of grid search

图2 模型回判精度图Fig.2 Recognition p robability of the trained classifier
为了进一步验证PCA-SVM模型的优越性,作者还运用判别分析模型和SVM模型,对表2的数据进行了相同的分类预测,结果见下页表4。
由表4可知,SVM虽然具有小样本、全局寻优、泛化能力强等优点,但输入数据的相关性对SVM的预测精度有较大影响:单独使用SVM的精度(93.6%)小于传统Fisher判别分析模型(96.3%);当使用主成份分析对数据进行预处理后,预测精度达到了100%。进一步分析表4,对于SVM模型判错的87号和92号样本,都是将储层识别为I类。作者认为,这可能是训练样本中I类储层样本个数较多所造成的,表明单独使用SVM模型,对训练样本的选取也有较高的要求。
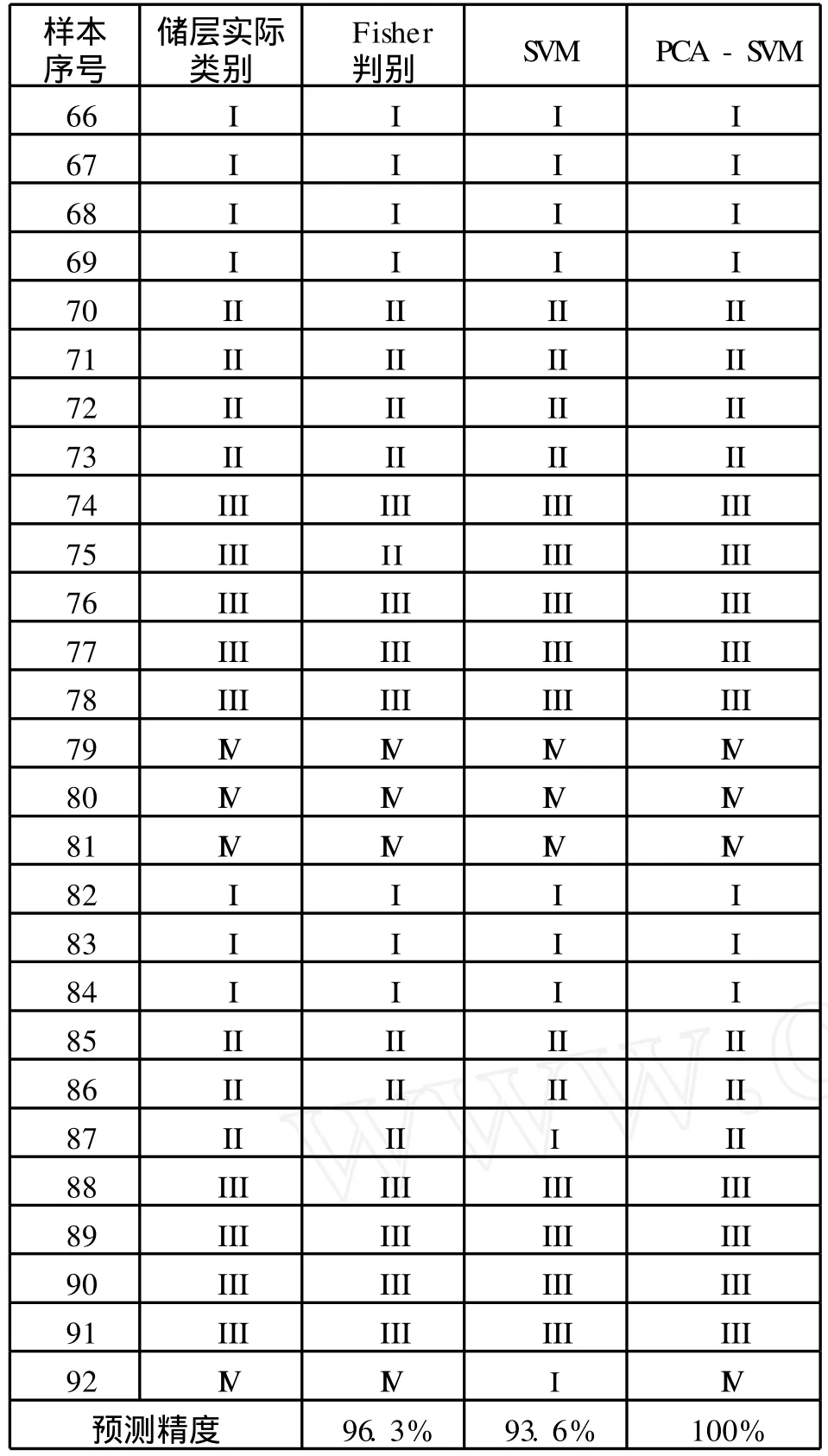
表4 预测结果对比表(加粗斜体表示预测结果与实际不符合)Tab.4 Resu ltsof p rediction
3 结束语
作者在本文提出的PCA-SVM储层识别模型,充分汲取了主成份分析和支持向量机的优点,不仅较好地解决了传统学习方法在非线性预测中的小样本、过学习、局部极小点等问题,还克服了自变量之间的多重相关性问题,减少了输入变量的个数,提高了预测精度和收敛速度。以中部气田马五1储层识别为例,采用PCA-SVM模型对储层类型进行预测,取得了良好的效果,预测结果与客观实际吻合。将该模型用于储层分类预测,丰富和发展了储层识别和预测的理论和方法。该模型在长庆中部气田马五1储层的识别中还仅仅是一次尝试,由于缺乏地震数据,作者只是对19口井的储层进行了纵向分析。在进一步的研究中,可以考虑利用单井精细预测结果与横向地震数据进行储层类别标定,对该区的有利储层进行横向预测。
[1]刘锡健,匡建超.偏最小二乘神经网络在储层识别和产能预测中的应用——以陕甘宁盆地中部气田马五1储层为例[J].矿物岩石,2005,25(4):80.
[2]李定军,李瑞.逐步回归法在川西坳陷须家河组四段储层识别中的应用[J].中国西部油气地质,2006,2(2):223.
[3]文环明,肖慈王旬,甄兆聪,等.动态聚类分析在储层分级中的应用[J].物探化探计算技术,2002,24(2):323.
[4]刘正锋,燕军.模糊识别方法在储层识别中的应用[J].西南石油学院学报,1998,20(3):4.
[5]田方,杨永发,麻平社,等.逐步判别分析法在鄂尔多斯盆地油田的应用[J].国外测井技术,2005,20(1):40.
[6]张银德,匡建超,曾剑毅.基于粒子群算法的模糊优选神经网络储层识别模型[J].物探化探计算技术,2008,30(3):202.
[7]匡建超,曾剑毅,王众.模糊优选神经网络在长庆中部气田马五1储层识别中的应用[J].油气地质与采收率,2008,15(5):5.
[8]张锋,张星,张乐,等.利用支持向量机方法预测储层产能[J].西南石油大学学报,2007,29(3):24.
[9]滕卫平,俞善贤,胡波,等.SVM回归法在汛期旱涝预测中的应用研究[J].浙江大学学报(理学版),2008,35(3):343.
[10]郭科,龚灏.多元统计方法及其应用[M].四川:电子科技大学出版社,2003.
[11]VLAD IM IR N.VAPN IK.统计学习理论[M].许建华,张学工,译.北京:电子工业出版社,2004.
[12]VLAD IM IR N.VAPN IK.The Nature of Statistical Learning Theory[M].NY:Sp ringer-Verlag,1995.
[13]刘得军,冉群英,王斌.支持向量机在大庆齐家凹陷测井解释中的应用[J].石油物探,2007,46(2):156.
[14]HSU CW,CHANGCC,L IN C J.A PracticalGuide to SupportVector C lassification[EB/OL].(2008-05-21)[2009-07-30]http://www.csie.ntu.edu.tw/~c jlin.
[15]董孝华,匡建超,齐天霞,等.陕甘宁盆地中部气田马五1储层流体识别及平面分布特征研究[R].西安:长庆石油勘探局勘探开发研究院,1994(12):52.
[16]洪楠,侯军,李志辉.M IN ITAB统计分析教程[M].北京:电子工业出版社,2007.
TE 122.2
A
1001—1749(2010)06—0636—05
四川石油天然气研究中心重点资助项目(川油气科SKA 09-01);四川省教育厅重点资助项目(2008ZB026)
2010-05-05 改回日期:2010-09-27
王众(1983-),男,四川成都人,博士,研究方向为矿产普查与勘探。
