未确知均值聚类

庞彦军,刘立民,刘开第

(河北工程大学 理学院,河北 邯郸056038)

聚类分析[1-2]是多元统计分析的重要方法,是模式识别的重要工具,在自动控制、系统辨识、人工智能、故障诊断等领域有重要的应用。基于迭代的动态聚类是最常用的聚类方法。C-均值聚类[3-4]是一种确定性聚类,是误差平方和最小意义下的最优聚类,当存在病态数据和分类不清数据时,聚类效果不能令人满意。模糊C均值聚类[5-6]则将隶属函数引入均值聚类,能很好的处理分类不清数据,但当样本存在“野值”时,效果不是很好。改进的模糊C均值聚类[7]等虽解决了“野值”问题,但迭代算法失去了可解释性。更重要的是,上述聚类算法没有充分利用输入数据提供的分类信息,没有体现出不同分类特征对分类作出的“不同贡献”。样本点之所以能被划分为不同类别,是由于不同样本的同一特征观测值不同。不同样本的某个特征观测值越接近,则该特征对区分开样本类别做出的贡献越小。样本集关于同一特征取值集中与发散的程度反映了该特征对分类贡献的大小,这是与分类“同时存在”的客观事实。本文分析特征对样本分类所作贡献,定义特征分类权重,给出计算样本关于各类隶属度的迭代算法,建立一种新的聚类方法—未确知均值聚类。

1 未确知系统理论[8]

未确知性是指由于条件限制,决策者无法确定事物的真实状态或真实的数量关系,因而产生的一种主观的、认识上的不确定性。对未确知性的定量描述和处理,是对人类主观事物范畴的一种探索。

定义1 设论域U={x1,x2,…,xn},F是U上的性质空间,E是F上的σ-代数,称(F,E)为U上的可测空间。

定义2 如果{F1,F2,…,Fk}满足

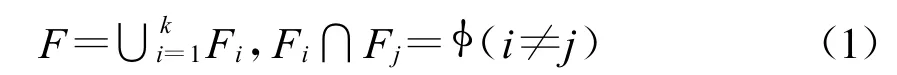
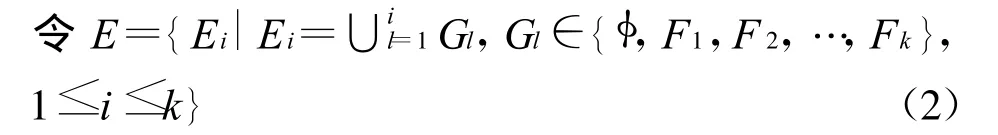
定义3 设(F,E)为U上的可测空间,μA(x)为元素x具有性质A的程度,如果对∀A,Al∈E,x∈U,有

则称 μA(x)为可测空间(F,E)上的测度函数,(U,E,μA(x))为未确知测度空间。

定义4 设(U,E,μA(x))是未确知测度空间,则以(x)为隶属函数确定了论域U上关于σ代数E的一个未确知子集G

当A∈E固定时,以 μA(x)为隶属函数确定了论域U上的一个未确知子集;当x∈U固定时,以μA(x)为隶属函数确定了 σ代数E上的一个未确知子集。所以,μA(x)是U×E上的二元函数。

2 未确知均值聚类算法

2.1 问题描述

已知d维特征空间的N个训练样本xi=(xi1,xi2,…,xid)(i=1,2,…,N),欲将 N个样本划分为C 类:Γ1,Γ2,…,ΓC。确定出 Γi类的类中心mi,则可用最小距离准则确定各样本点及待识样本点的类别。

2.2 基本假设

假设同一类中的样本点在特征空间中彼此应该更“接近”,并且这种“接近”是欧氏距离或加权欧氏距离意义下的接近[9],即认为同类样本点在空间呈现超球体分布。如果这种“接近”是指在某个方向上的接近,将对应“距离”的不同表达方法。

2.3 启发性知识获取

设xi=(xi1,xi2,…,xid)的分量是标称化数据。为了定量描述d个特征对初始分类做出的贡献,令

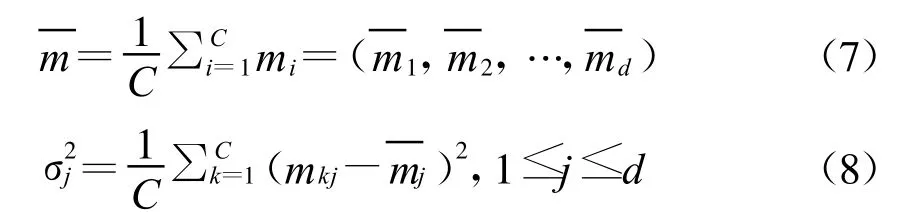
令

称ωj为特征j关于给定分类的分类权重。特征分类权重是在给定某种分类下,特征对“区分开”各类所做“贡献”在所有特征中所占的比例。

2.4 隶属度计算

初始分类给出C个聚类中心m1,m2,…,mC,任一训练样本xi关于以mk为类中心的Γk类有一个实际上的隶属度 μik。显然,μik与点xi到mk的距离及各特征的分类权重有关。当 ωj=0时,j特征对分类不起作用,这时分量(xij-不应作为距离分量出现在表征 xi到mk的距离中;而 ωj越大,j特征对分类贡献越大。所以,当用xi到mk间的距离Dik去表征xi关于Γk类隶属度时,这种“距离”应是一种加权距离。当样本点 xi到类中心mk的加权距离越小时,xi属于Γk类的隶属度越大。故

3 未确知均值聚类迭代算法

对 Γk类的类中心mk赋予质量 μik,令 Γk类的新类中心向量为以新类中心替代初始类中心向量,可以建立求类中心的迭代算法。

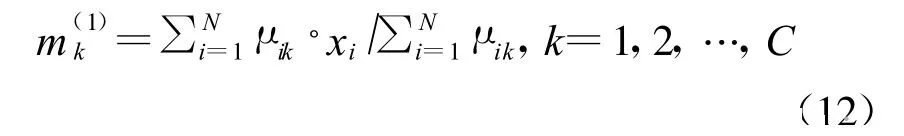
步骤1 对N个训练样本xi(i=1,2,…,N)的观测数据实施标称化变换,标称化后的无量纲数据记为xi=(xi1,xi2,…,xid);给定分类数C。

步骤3 由(7)、(8)、(9)式,得分类权重向量ω(0)=(ω(10),ω(20),…,ω(C0))。

步骤4 由式(10)与式(11),得隶属度向量 μi1,μi2,…,μiC)(i=1,2,…,N)。

步骤6 若maix‖＜δ,其中 δ＞0是预先给定得小正数,则迭代停止,所求的C个聚类中心为

4 有效性检验

对3类共150个样本的IRIS数据,采用密度法确定3个初始类中心,结合本文算法经10次迭代后求出3个聚类中心,然后对150个训练样本按“最小加权距离准则”重新归类。经15次重复实验,平均误识率为1.3%,表明本文算法稳定、实用、鲁棒性较好。

5 结论

1)未确知均值聚类根据样本关于各类隶属度与类中心间的内在联系,直接用迭代法求聚类中心,避开了构造准则函数,使得算法的每一步涉及的类中心与隶属度具有物理的可解释性。

2)未确知均值聚类充分利用了输入数据提供的关于分类的启发式信息,构造的隶属度严格满足测量准则。

3)IRIS数据检验表明,未确知均值聚类算法较模糊均值聚类算法误判样本数少且收敛速度快,是一种实用、有效的无监督聚类算法。

[1] MARQUES DE SA J P.模式识别—原理、方法及应用[M] .北京:清华大学出版社,2002.

[2] 顾洪博,赵万平.基于MMD聚类算法及在高校成绩分析中的应用[J] .河北工程大学学报(自然科学版),2010,27(1):96-98.

[3] 周巧萍,潘晋孝,杨明.基于核函数的混合C均值聚类算法[J] .模糊系统与数学,2008,22(6):148-151.

[4] 高新波,裴继红,谢维信.模糊C-均值聚类算法中加权指数m的研究[J] .电子学报,2000,28(4):80-83.

[5] 刘蕊洁,张金波,刘锐.模糊C均值聚类算法[J] .重庆工学院学报,2008,22(2):139-141.

[6] 陈佳妮,段文英,丁徽.模糊C-均值聚类分析在基因表达数据分析中的应用[J] .森林工程,2010,26(2):54-58.

[7] 刘坤朋,罗可.改进的模糊C均值聚类算法[J] .计算机工程与应用,2009,45(21):97-98.

[8] 刘开第,曹庆奎,庞彦军.基于未确知集合的故障诊断方法[J] .自动化学报,2004,30(5):747-756.

[9] 王 鑫,颜 炎,杨睿嫦,等.多批次测试数据建模新方法[J] .黑龙江科技学院学报,2010,20(3):227-229.