基于粒子群算法的电力系统经济负荷分配研究

徐中华 ，马 龙 ，杨 宁 ，吕培淑

（1.山东电力核电建设集团公司，山东 济南 250001；2.山东电力超高压公司，山东 济南 250021；3.山东电力集团公司，山东 济南 250001；4.青岛市平度仁兆中学，山东 青岛 266001）

0 引言

电力系统经济负荷分配 （Economic Load Dispatch,ELD）的目标是在不改变现有设备的条件下，在系统内合理分配各台发电机组所承担的负荷，以使总的发电费用最低。当所有机组都在最经济状态下运行时可以带来巨大的经济效益，它是经济调度中非常重要的问题，是电力系统中一类典型的优化问题。

传统的解决ELD的方法包括等微增率法，拉格朗日松弛法等经典数学方法，这些算法要求应用对象有良好的数学特性，而实际的经济负荷分配问题具有高维性、非凸性、离散性和非线性等特点，这使得经典数学方法处理ELD问题效果不理想［1］。近年来，随着人工智能技术不断发展，混沌优化算法［2］、遗传算法［3］等智能算法被广泛应用于 ELD 问题的求解中，取得了一定的效果。

由美国的Kenny和Eberhart在1995年提出的粒子群优化算法［4］（particle swarm optimization PSO）是一种源于对鸟群捕食的行为研究的进化计算技术。与其他智能优化算法相比，粒子群优化算法有以下几个优点：首先，算法具有很好的普适性，可以适应很多不同的应用环境；其次，算法的分布式能力很强，这是由于粒子群算法是进化算法中的一种，进化算法普遍具有这样的特点；第三，算法能够快速收敛；第四，粒子群算法可以很容易的与其他算法混合以进行改进，从而提高算法的性能。PSO算法已被应用于很多研究中［5-6］。本文将PSO算法应用于ELD问题的研究中，通过对实际经济负荷分配算例进行仿真，验证了该方法的有效性。

1 电力系统经济负荷分配的数学模型

1.1 目标函数

ELD问题在数学上可以表示为满足若干个等式约束和不等式约束的非线性规划问题，就是使价值函数最小，其价值函数为

式中：C为价值函数；n为系统内发电机总数；为第Pi台发电机的有功功率；Fi（Pi）为第 Pi台发电机发出有功功率 时，单位时间所需的能源耗量，即耗量特性。

发电机耗量特性曲线常用发电机有功功率的二次函数近似表示，即

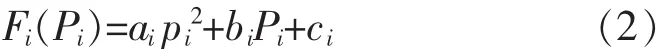
式中，ai、bi、ci为常数。

1.2 约束条件

经济负荷分配的约束条件主要考虑发电机的运行约束条件和功率平衡约束条件。

1）发电机的运行约束条件

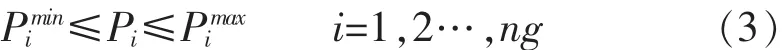
式中，Pimin，Pimax分别为第i台发电机有功功率的最小值和最大值。

2）功率平衡约束条件

式中，PL为系统内的总负荷;PS为系统的总网损。

1.3 发电机耗量曲线的阀点效应

在实际中，在机组热运行测试阶段，发电机的有功功率从最小值缓慢增加到最大值的过程中，机组的耗量曲线是起伏的，相当于在机组的耗量曲线上叠加1个脉动效果。造成这种起伏的原因是汽轮机的调节汽门随着发电有功功率的增大而依次开放所形成的，当上一级汽门已全开而下一级汽门刚开时，蒸汽的流通会因节流效应产生损失，而导致耗量增大，曲线向上凸起，这种现象称为阀点效应。

阀点效应可以表示为

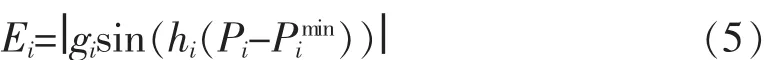
式中，gi、hi为常数。

2 粒子群算法

粒子群优化算法是一种源于对鸟群捕食的行为研究的进化计算技术。PSO中，每个优化问题的解都是搜索空间中的一只鸟，称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

PSO算法初始化为一群随机粒子，即随机解，然后通过叠代找到最优解。在每一次叠代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解。这个解叫做个体极值pBest.另一个极值是整个种群目前找到的最优解。这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。在找到这两个最优值时,粒子根据一定的公式来更新自己的速度和位置。

在PSO中，假设由N个粒子搜索Q维空间，每个粒子的位置可表示为：xi=（xi1，xi2，…，xiQ），速度可表示为 vi=（vi1，vi2，…，xiQ）。 粒子需要跟踪的两个极值是单个粒子的历史最优位置Pi和所有粒子的全局最优位置Pg，找到这两个位置后，粒子更新自己的位置，其更新公式为

式中，ω是保持原来速度的系数，称为惯性权重；c1是粒子跟踪自己历史最优值的权重系数，它体现了粒子对自身的认知能力；c2是粒子跟踪群体最优值的权重系数，它体现了粒子对整个群体知识的认知能力；μ、η 是［0，1］区间内均匀分布的随机数；ρ是对位置更新时，与速度有关的一个系数，称为约束因子，通常设置为1。

粒子群算法的基本流程如图1所示。

如图1所示，粒子群算法步骤如下：

1）初始化群体微粒（群体规模为N），包括随机位置和速度，并将每个粒子的原始位置设置为原始速度设置为。

2）求出每个微粒的适应值。

3）对每个微粒，将其适应值与其经过的最好位置xi（Pi）时的适应值作比较，如果较好，则将其作为当前的最好位置 xi（Pi）。

4）根据公式（7）-（9）更新微粒的速度和位置。

5）检查各变量是否溢出各自的取值范围。如果高于其上限值，或低于其下限值，则用相应的边界值替代。

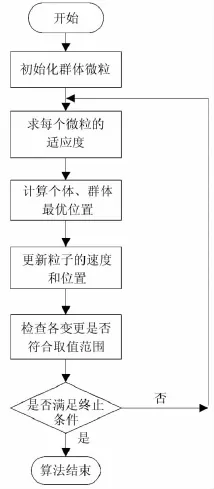
图1 粒子群算法流程图

6）根据终止条件判定是否终止迭代。如果满足终止条件则终止迭代，否则返回（2）继续迭代过程。

3 算例及仿真结果比较

本文仿真算例采用文献［2］的3机6母线系统实际算例，发电机承担的总负荷为500 MW，考虑阀点效应，不考虑系统的网损。各发电机的耗量特性及有功功率极限值如表1所示。

表1 各发电机耗量特性及有功功率极限值

采用PSO算法进行仿真，各参数分别为：粒子数目N=40，迭代次数为kmax=100，惯性权重w=0.729，c1=c2=1.4962，r1、r2为 0到 1之间的随机数。仿真结果如表2所示。

比较表2中数据可以看出，与ELD的传统算法相比，采用PSO算法后，总费用减少34.60$，总费用改善程度明显。可见PSO算法是具有一定的优势的。

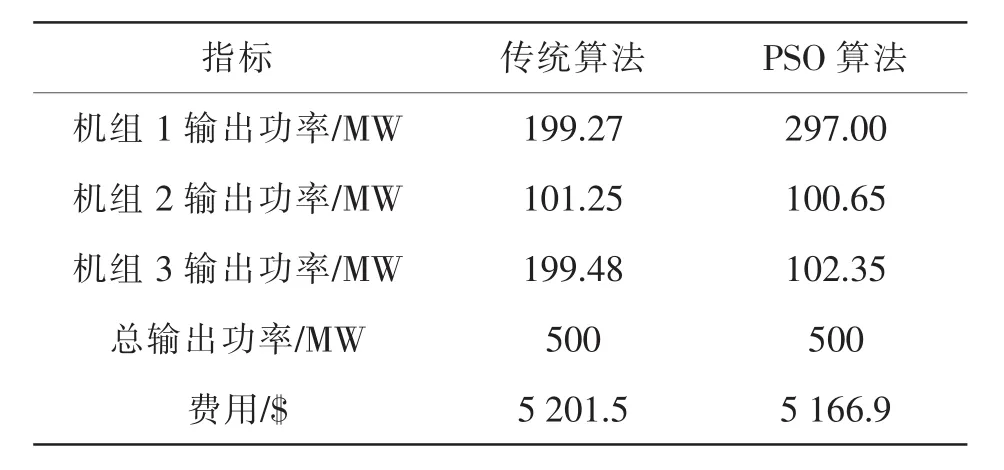
表2 PSO算法的算例仿真结果

4 结束语

本文将粒子群算法用于电力系统经济负荷分配中，取得了以下结论：1）粒子群算法是一种源于对鸟群捕食的行为研究的进化计算技术，具有全局优化能力强、收敛性好和编程实现简单等优点。2）将粒子群算法用于电力系统经济负荷分配中，可有效解决经济负荷分配问题，从仿真情况看，可获得较满意的解，为粒子群优化算法的进一步实用化奠定了基础。

［1］AI-Sumait， J.S.AL-Othman，A.K.； Sykulski； J.K.Application of pattern search method to power system valve-point economic load dispatch ［J］.International Journal of Electrical Power and Energy Systems,2007,29（10）:720-730

［2］唐巍，李殿璞.电力系统经济负荷分配的混沌优化方法［J］.中国电机工程学报，2000（10）：36-40.

［3］何大阔，王福利，毛志忠,等.遗传算法在电力系统经济负荷分配中的应用［J］.系统仿真学报，2007，19（4）:890-892,900.

［4］Kennedy J，Eberhart R.A new optimizer using particle swarm theory［C］.Proceedings of the sixth international symposium on micromachine and human science，1995:39–43.

［5］杨波，赵遵廉，陈允平，等.一种求解最优潮流问题的改进粒子群优化算法［J］,电网技术，2006，30（11）：6-10.

［6］沈广，陈允平，刘栋.改进离散粒子群算法在冷负荷启动的配电网馈线恢复中的应用［J］，电网技术，2006，30（7）：55-58.