重新审视井碰概率

2010-10-13编译唐可伟西南石油大学研究生院

石油石化节能 2010年9期

关键词：概率密度函数马氏井段

编译:唐可伟 (西南石油大学研究生院)

审校:李甫 (西南石油大学研究生院)

重新审视井碰概率

编译:唐可伟 (西南石油大学研究生院)

审校:李甫 (西南石油大学研究生院)

鉴于意外井碰导致的灾难性的人类和环境损害,一个关于井眼碰撞概率的评价提供了一种宝贵的风险管理方法。目前工业上使用的评估技术不少,但都有其局限性。解决问题的一个合理方法是开始就明确地估计井碰概率。本文提出了一种方法,以确定所钻井特定井段与邻井相交的可能性。通过对参考井上连续井段相关可能性的综合考虑,可以得到总的碰撞概率。井碰概率的估计是基于已测井眼轨迹及测量不确定性的知识,并以位置协方矩阵的形式来表达。本文研发出一个更精确的碰撞概率评估方法,此方法克服了以往方法的限制。实例表明, 2口井在相交区域都是垂直的情况下,此新方法与平行和非平行井眼轨迹的分析结果相一致。

井碰概率马氏距离数值积分概率稀释

1 介绍

近期的重点是模型的改进,此模型用于描述测量的精确性和测量数据的质量控制。这些测量数据和合适的误差模型为评估碰撞概率提供了基础。Thorogood等人 (1990年和1991年)、Brooks和Wilson(1996年)、Roper和 Henly(1996年),以及Tsao等人 (1999年),已经描述了通过对二维或三维概率密度函数积分来解决问题的方法。必须认识到,井碰概率的数值估计不可能比推导它的数据更可靠。

2 问题描述

现有的资料包括2口井的测量数据以及与这些数据相关的不确定性,这些数据是以测量误差模型或位置误差的协方差矩阵形式表示的。该测量不确定性可根据标准方法 (Brooks和 Wilson,1996年;Williamson,2000年;Torkildsen等人,2008年)估计参考井上的一点和目标井上另外一点之间相对位置的不确定性。而两点间的相关不确定性过去常用于评估井碰总的概率。这种不确定性以一些标准偏差表示,对某一给定的误差分布,它们可以转换为概率密度函数。碰撞概率的建立是通过整合表示参考井和目标井中巨大风险的所有点的密度函数可能性来实现的。

3 基本原理

测点的位置以空间的点来表示。根据适当模型(一般为最小曲率)在这些点之间进行插值,给出了每个井眼轨迹假定的中线轨迹。如果参考井段的中线在目标井井眼轨迹中线的一定范围内,就会发生碰撞。这个临界距离就是2口井半径之和。因此,可以想象,目标井就是一个半径等于2口井半径之和的圆柱体,如果参考井段的中线有可能穿过这个圆柱体,那么就会发生碰撞 (图1)。通过为目标井指定两个直径,并结合相关位置不确定性,我们只需要关注参考井中线上一点的唯一不确定区域。

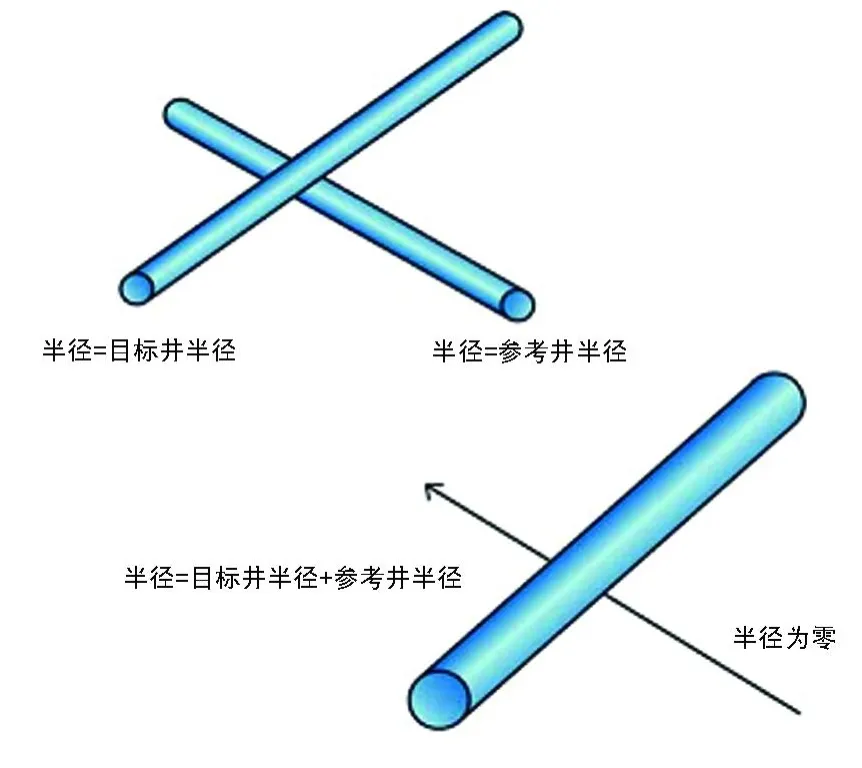
图1 相交井眼轨迹等价表示

目标井的位置与参考井段从何处开始有关,可以用一个圆柱体表示,其半径是井半径之和。当沿着参考井段前行观察时,目标井的相对位置以相反的方向变化。因此,当沿着参考井向西移动时,目标井的相对位置向东移动。于是,提出了这样的问题:参考井段应该从哪个位置开始才穿过目标井?这些位置的建立是通过沿着与参考井段相反轨迹来投影目标井圆筒的。

当将所有沿着参考井段的点都应用到目标井圆筒时,其投影绘制出了一个体积,它是一个三维板,其中两个相反的面受到目标井管道形状的限制,另外两个面由与参考井段相反的形状确定。而且,其厚度是所有井直径的总和 (图2)。在参考井段开始处,与目标井相关位置相邻的面是一个凹形圆柱体,而其反面则是一个凸形圆柱体。如果参考井段的初始位置恰好位于此体积内,就可能在参考井段内发生碰撞。

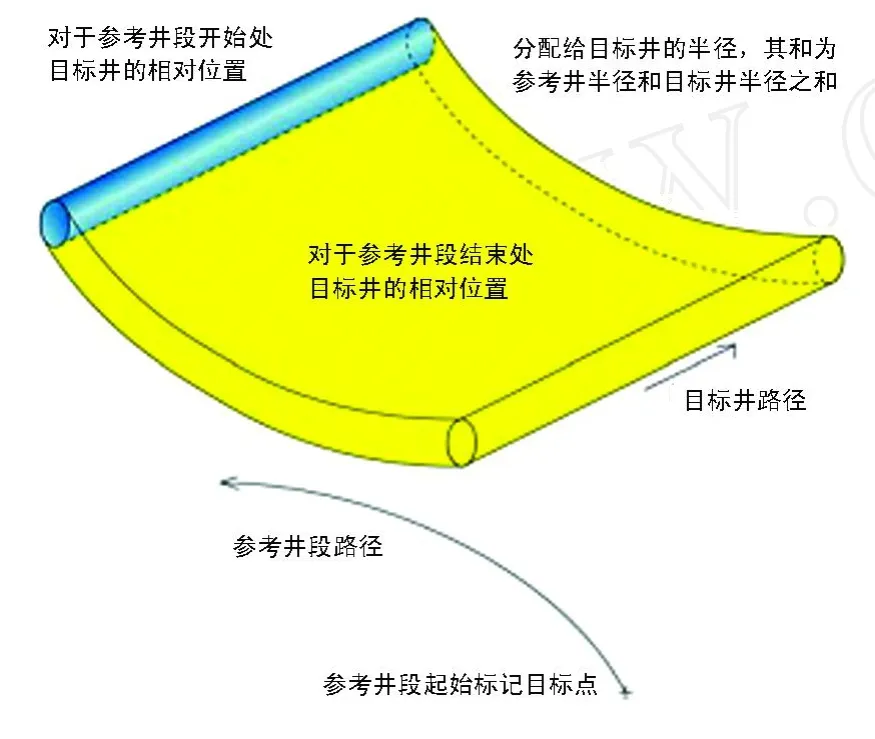
图2 目标井相对位置波及的体积

为了估计井碰概率,对所有井使用相对不确定性,以创建参考点可能性区域。这个可能性区域可被认为是一系列同心的椭球表面,每个面包含的点都与原点具有相同的标准差,得到三维概率密度函数的轮廓线。轮廓线由以下方程式表示

式中,r是一个矢量,它定义了相对于参考井段初始位置的目标点的位置;C是目标井中原点和目标点间定义相对不确定性的位置协方差矩阵;k是一个比例因子,它以一些标准差表示距离,也称作马氏距离 (图3)。为了列举出给定体积中一个点可能的位置,有必要确定误差分布。工业上普遍的做法是利用高斯分布,这里也将这个高斯分布用到目前的例子中,此方法也适用于误差分布。误差分布定义了概率密度函数,它将概率密度与马氏距离联系了起来。目标体积里参考井段开始处的概率可以通过对体积上三维概率密度函数积分而建立,这样得出碰撞概率的近似值。

3.1 基本解决办法的局限

虽然实现起来有些困难,但这一过程还是提供了一种简单而又完整的一般三维问题的解决方案。然而,由于在2口井中用到了不变的不确定区域,积分结果最多也只是一个近似值。如果不确定区域在目的层段上变化不大,那么对相交来说结果是合理的;如果确定2口井是平行的或者是并排的话,就不能采用这种简单方法。在平行井的情况下,井碰危险性的增加完全在于测点的不确定性,它必须在相对不确定性中有所变化。如果没有测点的不确定性,那么测量的水平井就的确是平行的,没有任何碰撞发生。

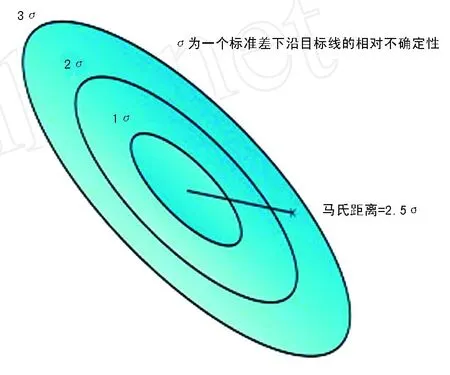
图3 马氏距离

4 模拟天体动力学

研究油井相交与宇宙飞船碰撞有很多相似的地方。特别是,指出了天体运动学中短周期或线性相交与长周期或非线性相交之间的区别。短周期或线性相交中卫星轨道的关键点假定是直的,而且不确定位置不变;长周期或非线性相交中必须认为轨道是弯曲的或者不确定位置是变量。总的来说,非线性问题可以通过对三维概率密度函数积分来解决,而线性问题则可以降为二维问题。短周期的宇宙飞船的相遇和近似于常量的相对位置不确定性的直的井眼轨迹的相交,二者之间非常相似;同样,长周期宇宙飞船的相遇和弯曲井或变化的相对不确定性的井眼轨迹的相交很相似。

航空与油田上的应用最主要的区别是,参考井不仅仅要避免与目标井中的一点相交,它必须得避免与整个目标井井眼轨迹相交。这就意味着,几乎所有的油井问题在相交区域都将涉及到弯曲的井眼轨迹或变化的位置误差的协方差矩阵,因此必须将它们看做是需要三维积分来解决的非线性问题。

4.1 转换为马氏空间

目标井的目的层段包括了一些被认为碰撞概率很高的点,这通常包括参考井段中6个标准差以内的点。对于参考井目标点和与此相关的相对确定区域来说,目标井中每个已测点都是可知的。对于可能性区域来说,点的位置才是重要的,而不在于它在空间的什么地方。当移动到2口井中另外一个点时,相对不确定性可能会有所变化,因此相交的位置也可能会改变。如果能够将目标井中点的位置标准化,以使它们相对于变化的可能性区域是固定的,那么通过一个包括许多点的不确定体积就可以表示目标井,所有的这些都被绘制在同样的可能性区域里。位置的标准化是通过将椭圆体区域减小为球体区域来实现的,其结果图图2相似,但在空间上它是用标准差来衡量而不是单位长度。这个空间就是马氏空间,其中从原点到任何点的距离就是马氏距离k,相当于从原点的标准差的数量。

转换为马氏空间是通过重新调整椭圆体区域使主轴相等 (图4)实现的。这个过程对位置协方差矩阵C进行波谱分解,分解成一个旋转矩阵V和一个缩放矩阵E,这里体积V是C的特征矢量,E是一个包含特征向量C的对角矩阵。

而且在正规空间A点与向量r相一致,并由与马氏空间的Tr一致的点表示,这里的变换矩阵 T由公式给出。

T是真实空间和马氏空间之间的转换矩阵。这是一个仿射变换,在其变换下直线被保留,但角度可能改变,圆管表示的目标井可能会变成椭圆。

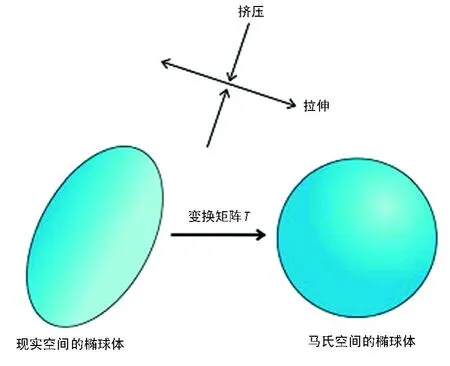
图4 转换为马氏空间

4.2 数值积分

概率密度与体积中表示目标井的每个点相对应。目前常见的做法是假定高斯误差分布,尽管人们认识到这未必是最佳的。

对与目标井一致的整个体积的概率密度函数进行积分得到了一个很有用的结果,这是目标点的概率,这种情况下参考井段的原点可能与目标井相一致。在参考井中,更多的还是关心钻前特定井段井碰概率的增加。尤其是当钻进时,参考井段就是连接管道,或是立管到下个测点的距离。当规划好了一口井后,也许将用到更长的井段,以包含所有可能的碰撞。这样,参考井段可能包括沿参考井的所有点,这些点在6个标准差内达到目标井的测量位置。

因此,这个过程必须遵循沿参考井段的一系列点。在马氏空间中,对于每个点,目标井中的目的层段是以体积表示的。该体积中加入了另外的体积元素,以前的步骤中沿参考井段并没有这些元素,这意味着可能引起参考井段当前阶段潜在井碰的发生。在当前阶段,对这些新元素的概率密度函数的积分表明井碰发生可能性的增加。除目标井初始位置以外,图2中增加的阴影体积就是目标体积,其在马氏空间中绘出。

对所增加体积进行评估最方便的做法就是将其分成体积元素。沿参考井每个步骤完成之后,就会增加一些新的元素。第一个方面,这些元素可能近似于六面体,与沿参考井的距离一样长;第二方面表示目标井的步长;第三方面表示井直径之和。如果表示沿参考井段步长的尺寸被与目标井正交的它的投影替代的话,体积元素可以处理成大致正交。当保持这些元素大致等量纲时,将允许使用沿着参考井段更长的步长。井碰概率可以计算为每个新元素与形心上概率密度乘积的总和。保证元素大致等量纲对计算效率有利,因此沿着目标井的步长也许可以与井径之和大致相等。有时候需要将体积元素进一步细分,Alfano建议尺寸可以小到标准差的1%,以得到精确的结果。通过在最后一步包括半管表示目标井,而在第一步去除半管的方法也可以提高结果的精度。这些椭圆半管可以通过多面体体积元素近似得到。

5 实例

上述方法可以解决大多数井眼轨迹相碰的问题。文中用了两个简单的实例来说明该方法适用于一系列广泛的问题,其得到的结果也很容易理解。解析表达式也来自通行方法,以解决这些特殊情况。

5.1 非平行直井,不确定性恒定

如果沿着目的层段的相对不确定性变化较小,就不需要将其转换到马氏空间,可以直接在真实空间积分。如果在目的层段的目标井垂直延长超过6个标准差,就可以认为在每个方向上无限延伸,而对结果没有明显的影响。沿着目标井上的积分得到了统一,井半径可能被赋值给参考井段并投影到正交于目标井的平面 (图5)。在此平面上,对二维概率密度积分的面积是一个圆角矩形,其长等于参考井段,宽等于井直径之和。此井段内井碰概率是面积上二维概率密度函数的积分。如果参考井段足够长和直,那么问题就可以变成一维;并且,如果假定为高斯误差,则井碰概率是对高斯概率密度函数的积分:

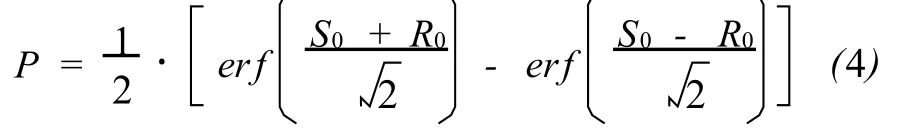
式中无量纲井距和半径分别是S0和R0。S是马氏空间中无因次距离;R是马氏00空间中无因次的半径之和;S是参考井和目标井点之间的距离,σ是一个标准差下的相对位置不确定性,二者都是在与2口井正交的方向上测定的。Williamson(1998)、McNair(2005)和 Poedjono (2007)等人提出的方程 (4)是更精确的表达式。

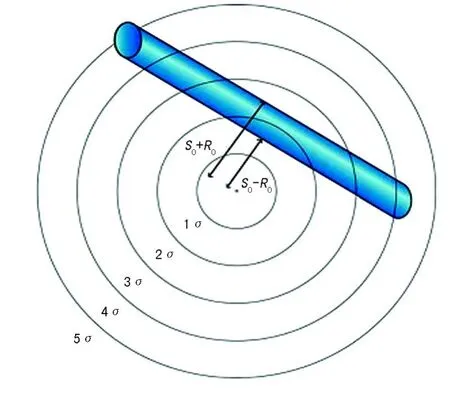
图5 与目标井正交平面上的参考井段

5.2 并排直井,不确定性变化

第二个简单的例子是并排的直平行井,这样的情况在直井的近地表处产生。为了提供一个有用的例子,有必要沿着井眼轨迹改变相对不确定性。

此例中,假定测量误差是方位对称的,这样在马氏空间中目标井看起来像个圆管。由于在重大危险井段目标井是直的,可以认为它是无限延伸的,则三维表示可以变成与目标井正交的二维表示,它看起来像一个圆。随着沿参考井深度和相对不确定性的增加,当它靠近初始位置时,目标井的投影似乎在缩小。这是因为直径和距离在真实空间中保持不变,但是测量单位 (标准差或位置不确定性)变大了。如果所有测量误差都是对称的,不确定性将与深度严格成正比。最后,取沿参考井足够长的井段,目标井映射的区域大致为一个扇形,张角为2sin-1[(rr+ro)/S],式中rr和ro分别是参考井和目标井的半径,S是名义中线距离。

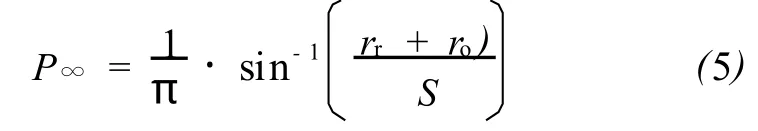
这种解决方法可能出人意料,但它是基于准确测量的。从直观来说它是合理的,因为已假定所有测量误差都是对称的。因此,虽然它们与所测量的矢量方向可能并不完全一致,但所有可能的井眼轨迹都是直线。朝向目标井所在区域的井眼轨迹的方位角最终将与井眼轨迹碰撞。井眼轨迹的方位角朝向的可能性只是圆的很小的一部分,而圆是名义距离的井直径之和所形成的,由方程式 (5)给出。虽然这个例子给出了一个很有用的确认方法,但它在现实中却具有局限性,因为实际问题中将会强制给出一个参考井段的最大深度。

6 概率稀释法

有时计算的井碰概率可能会因测量准确度很差而使得数值估计结果失常。Thorogood(1990)和航空领域的Alfano(2003、2006a、2008)已经提到过这个问题。以方程式 (4)举例,假定2口井相交的测量距离为20 m,井半径之和为0.3 m。如果相对不确定性的标准差是10 m,据计算井碰概率为3.2×10-3;当标准差是20 m时井碰概率为7.×10-3,但是如果标准差为50 m时,井碰概率又降为4.4×10-3。这个现象被称为“概率稀释”,由Alfano(2003、2008)提出。他指出,当估计的概率落入概率稀释区域内时,此概率就不能使用,因为测量质量不足以提供一个有意义的井碰概率的估计;同时他也建议到,应该尽可能围绕在产生最大井碰概率的地方设定不确定性进行工作。