一种提高复杂井况下管柱设计系数的三轴应力方法

2010-10-13编译王建军王同涛审校林凯闫相祯

石油石化节能 2010年5期

关键词：计算公式管子管柱

编译:王建军王同涛,审校:林凯闫相祯

(1 中国石油天然气集团公司管材研究所,石油管工程重点实验室)

(2 中国石油大学 (华东)储运与建筑工程学院)

一种提高复杂井况下管柱设计系数的三轴应力方法

编译:王建军1王同涛1,2审校:林凯1闫相祯2

(1 中国石油天然气集团公司管材研究所,石油管工程重点实验室)

(2 中国石油大学 (华东)储运与建筑工程学院)

利用von Mises屈服判定准则和拉梅厚壁圆筒理论,建立了管柱在复杂工况下三轴应力强度精确计算模型,考虑了内外压力、轴向载荷、弯曲和扭转等载荷影响,全面分析了管柱破坏时的管柱应力状态,这是对传统三轴应力分析方法的一种改进。由于采用无量纲化的公式推导方法,本文建立的模型适用于所有材质和尺寸的管柱设计计算,推导得到的挤毁载荷计算公式适用于径厚比小于14的管子,且认为管子屈服破坏开始于内壁;破裂载荷的计算公式适用于所有尺寸的管柱。

管柱应力精确计算模型管子破裂和挤毁

1 引言

现在钻井技术中有很多用于计算钻井、完井和试油时管柱受力的计算模型,由于每种模型基于的原理和考虑的因素各不相同,使得计算结果不便于进行有效的比较。因此,本文给出了一种精确的三轴应力管柱受力计算模型,以Lubinski研究塑性椭圆模型为基础,全面考虑轴向载荷、内外压、弯曲和扭转等影响,对传统三轴应力设计方法进行改进。推导的计算公式可用于计算所有尺寸规格的套管破裂极限压力值和径厚比小于14的套管挤毁极限压力值。

2 三轴应力设计

在很多研究中忽略了剪切应力的影响,把轴向应力σz、径向应力σr和环向应力σh作为三个主应力来考虑。本文规定拉应力为正,压应力为负,则可以得到基于von Mises变形能理论的等效应力表达式:

若令σr=0和σh=0,则式 (1)变为:

定义设计系数 (DF)为材料的许用应力与工作应力的比值(σy/σVME)。当管柱工作应力为von Mises等效 (VME)应力时,许用应力可选用管材屈服强度。当DF=1时,理论上认为管柱已经失效。因此,在实际设计过程中DF越大,管柱抵抗失效的能力就越强。即DF表达式为:

1986年,Kastor建立了 Kastor模型,实现了三轴应力方法在管柱设计中的应用,正确解释管柱工作屈服问题,但是整个公式比较繁琐。1987年, Johnson、Jellison和 Klementich对 Kastor公式进行了简化,得到以下计算公式:

式 (4)是一个非线性函数,求解过程比较简单,适用于求解薄壁圆筒问题。通过无量纲分析方法简化了式 (4)的求解过程,假设管柱不受扭转或弯曲作用,引入几何形状参数β,则推导出下面的公式:

管子内壁的径向和环向应力的表达式为:

考虑到弯曲的影响,轴向应力的计算公式为:

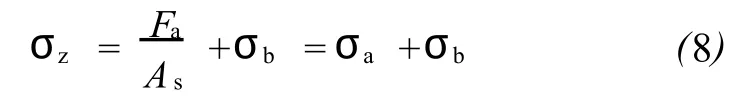
通过无因次量纲分析,可以得到下面无因次变量:

把式 (9)和式 (10)带入到方程 (3)中,则设计系数可以表示为:

式 (11)是一种计算管子破裂和挤毁载荷的精确方法,可取代式 (4)的近似算法。式 (11)完整地描述了管柱在轴向应力、内压和外压载荷作用下的屈服极限关系,形成三维屈服面(x,y,z)(图1)。

图1 三维屈服面

如果令z=1,则式 (11)表示作用在管子上的三向应力(σz、σr和σh)产生的等效应力等于管材屈服强度。图1中,在z=1下面的部分表示VME应力超过管材屈服强度;z＞1的部分,表示VME应力值小于管材屈服强度,也是安全设计系数的取值区域。在原点处的管子屈服应力趋于无穷大,此时σz=-pi、pi=po,即管子处在静水压力状态。

图2 三轴应力状态下设计系数在平面内的投影

图2所示的二维屈服面包络图,是采用不同z值平面对三维屈服面切割而得到。在包络图中,随着设计系数的增加,所包络的破裂压力和挤毁压力极限值不断减小,套管或油管服役载荷路径全都应在椭圆形区域内。若把管柱服役VME应力曲线绘制在同一张图中,可以发现管柱可能泄漏的位置点和危险工况。椭圆的上半部分对应于管子破裂压力,下半部分对应于管子挤毁压力。

由式 (11)可得:

在上式中,管子破裂时的环向应力取“+”,挤毁时取“-”。令DF=1,并把式 (9)和式(10)带入式 (12)中,可以得到:

挤毁压力极限载荷公式:

破裂压力极限载荷公式:

上述公式的推导过程中假设管子屈服失效始于管内壁。如果管柱中有弯曲作用,该假设就不成立,需要分析管柱外壁上的弯曲应力 (在外壁上最大),通过计算VME应力,可确定管柱内外壁哪一个先达到屈服破坏。

3 简化模型与精确模型的对比

下面对用简化解公式 (4)和精确解公式(13)、公式 (14)的计算结果进行比较 (图3)。管柱破裂压力的无因次当量计算公式为:

式 (15)和式 (16)的计算结果如图3所示,当压力变异系数较小时,简化解与精确解的结果误差比较小;当压力变异系数较大时,两者的误差就比较显著,可以达到10%或更高。

管柱挤毁压力的无因次当量计算公式:

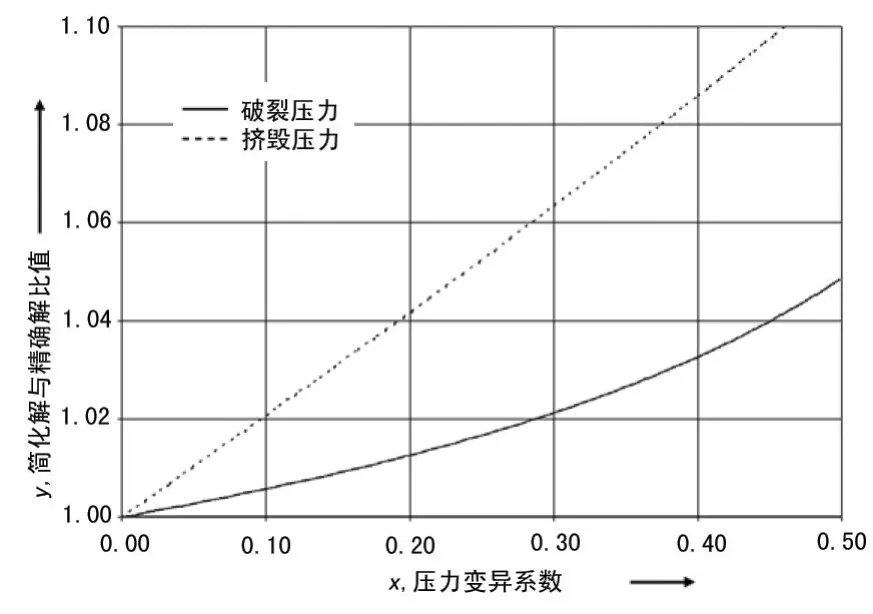
图3 两种计算公式得到结果的相对误差 (31/2in 15.5 lb/ ft钻杆,β=4.47,σz/σy=0.5)

4 扭转、弯曲和屈曲效应

轴向应力计算公式σz=σa+σb中,σa为轴向载荷与管子横截面积的比值,σb为弯曲产生的轴向应力。下面公式推导中,定义管子实际受到的轴向力为FA,浮力产生的虚拟轴向力为Ff,剪应力τ和弯曲应力σb在管外壁上同时达到最大值。

McSpadden和 Newman在2002年对von Mises变形能理论作了修改,考虑了剪应力的影响,即:

定义无因次当量剪应力为:

由拉梅公式可以得到管外壁径向应力σr=-po和环向应力σh=(β-1)(pi-po)-pi。由式 (17)可以得 (τD可由管子外壁计算得到):

同样可以得到与式 (19)类似的管内壁无因次应力表达式,最终可以得到管子内、外壁VME应力之差为 (外壁减去内壁):

当τD＞时,σVME在管外壁上达到最大值。

图4绘出了3个典型β值时,的关系曲线。y为负时表示管柱挤毁,y为正时表示管柱破裂。取β=7曲线的挤毁段 (图4)为例进行说明,即y=0.5,τD=0.6时,管柱内、外壁上的应力相等;在图形左右两边,表示管柱失效分别以挤毁和破裂为主;在图形中间部分,管子失效以扭转剪切破坏为主。

双轴应力椭圆被直线x=y分为两个区域 (图5),在直线上,轴向应力与环向应力相等;在直线上方,环向应力 (由内外压力产生)占主导作用;在直线下方,轴向应力 (由拉伸和压缩产生)占主导作用。

图4 考虑扭转时管柱内、外壁失效模型曲线

图5 双轴应力椭圆中轴向应力与环向应力的关系

5 算例分析及结果讨论

按照上述理论,分析了3口高温高压井管柱受力情况,计算中所要用到的数据见表1。

5.1 算例1

假定井口压力为68.3 MPa,完井管柱为5 in套管,套管柱下入过程中需要施加轴向载荷,经计算套管柱无因次轴向应力为-0.341(表1)。考虑到井口高温的影响,C95套管的屈服强度折减为577 MPa。

表1 3口高温高压井数据

由式 (9)、式 (10)和式 (11)分别计算出x=-0.341、y=-0.682和DF=1.7。通过x和y值可以找到它在图5中对应点的位置,位于图形中的左下方区域,可以推断套管柱受到的压力适中,不会发生挤毁破坏。

如果在下套管柱时,套管柱底部不密封,套管柱就不受轴向压力作用,y=-0.682保持不变,则可以计算出x=0、DF=1.5,同时在图5中找出对应点的位置。可以发现,高外压和适中的轴向压力组合具有很大的优势。

5.3 算例2

假设在套管外壁上弯曲应力为屈服强度的60%,即:σb/σy=±0.60,可以计算出套管内壁上无因次弯曲应力为令y=-0.682并结合例1中的数据可以计算出在套管柱内壁上x=0.144(表明σb为正值)和x= -0.826(表明σb为负值)。从图2中可以发现,点 (0.144,-0.682)和 (-0.826,-0.682)都在DF=1.3时的双轴应力椭圆上。同理,在套管柱外壁上取x=0.259和x=-0.941,可以发现两个点在DF=1.4的椭圆上。可见,即使弯曲应力在套管柱外壁达到最大值时,套管柱内壁上的应力还是大于套管柱外壁上的应力。

5.5 算例3

假设在近井口处油管泄漏,使得井口压力进入生产套管 (油套环空),封隔器上部流体密度为

1.18 kg/L,因热膨胀作用在套管柱上产生较大的轴向压缩载荷,可得套管柱在井底 (封隔器上部)的轴向应力可以达到-214 MPa(-0.273σy),如表1所示,套管内压等于井口压力与封隔器上部流体 (钻井液)静水压力之和,外压为外部地层液体压力。

利用本文建立的三轴应力模型可以计算出σVME=710 MPa,DF=1.11,可见为了提高设计安全系数,可以适当增加钻井液的密度。而利用传统的三向应力模型计算出来的σVME=739 MPa, DF=1.06,比真实的等效应力值大5%,在复杂井况套管柱设计中误差较大,建议使用精确三轴应力计算模型。