用非结构化网格模拟器模拟聚合物驱
2010-10-13编译周长江西南石油大学研究生部
编译:周长江 (西南石油大学研究生部)
审校:施雷庭 (油气藏地质与开发工程国家重点实验室·西南石油大学)
用非结构化网格模拟器模拟聚合物驱
编译:周长江 (西南石油大学研究生部)
审校:施雷庭 (油气藏地质与开发工程国家重点实验室·西南石油大学)
描述了用非结构化网格模拟聚合物驱的研究进展。聚合物驱模拟涉及到很多专业问题:聚合物溶液黏度 (具有剪切稀释或剪切增稠的特性)是聚合物浓度、剪切速率、矿化度和油藏温度的函数;聚合物的流度控制能力受近井地带高速剪切的影响;聚合物的热力学降解是聚合物浓度、矿化度和油藏温度的函数;聚合物的滞留会影响其流动特征。除此之外,文中还提供了方程的数值解法及其应用实例。
聚合物驱 模拟 非结构化网格
1 引言
聚合物驱已经在油田大规模应用,其概念很简单,即在注入水中加入少量水溶性聚合物以增加注入水的黏度,实现有利的流度比,从而提高水驱效果;但是,其机理是很复杂的。聚合物溶液黏度受聚合物浓度、矿化度、温度及剪切速率等因素的影响;吸附和滞留降低了聚合物浓度和水相渗透率;降解作用使聚合物丧失其增黏能力。因此,合理的聚合物驱设计和评价必须结合油藏特征、室内实验、油藏模拟、工艺技术及矿场试验。其中,准确的油藏模拟是聚合物驱设计和效果评价的关键。
从20世纪60年代后期开始,很多学者进行了聚合物驱数值模拟研究。1968年,Zeito提出了一个简单的聚合物驱数学模型:水相黏度是聚合物浓度的函数。1969年,Jewett和Shurz根据近60个聚合物驱项目,开发了一个两相、多层、能够模拟一维介质和五点井网的模拟器。1970年,Slater和Farouq Ali采用阻力系数经验公式和差分方法模拟五点井网聚合物驱。Bondor和 Hirasaki(1972年)以及Hirasaki和Pope(1974年)开发的数学模型认为聚合物只溶于水中,他们用修正的Blake -Kozeny模型并考虑了聚合物吸附、渗透率下降系数和聚合物溶液非牛顿流变特性的影响。1976年,Vela、Peaceman和 Sandvik开发的模拟器考虑了聚合物滞留、不可入孔隙体积、剪切降解和矿化度的影响。许多学者还考虑了化学降解和热力学降解对聚合物溶液特性的影响。
20世纪80年代以来,油藏模拟变得越来越复杂,对计算的准确性要求也越来越高。通过对工艺技术和流线的研究,现代油藏模拟力求实现对细小裂缝、复杂井眼轨迹等多方面的影响因素进行模拟。与常规网格系统相比,非结构化网格系统能够获得更多、更准确的地质和工程信息。对常规网格系统的研究比较成熟,而关于非结构化网格系统的研究却较少。2001年,Beckner等人为ExxonMobil公司开发了非结构化网格模拟器,并对一个拥有复杂地质裂缝和多个油藏、采用常规工艺技术生产的油田进行了模拟。研究结果表明:大约10万个非结构化网格就能实现相当于160万个正交网格才能实现的地质裂缝的准确模拟,所以该模拟器简单易用,大大缩减了模拟时间。
常规油藏模拟的基本方程见附录A(附录见原文,下同)。这些方程中包括体积守恒方程和组分摩尔守恒方程。总体积守恒方程A-8用来求解压力,各相体积守恒方程A-7用来求解相饱和度,摩尔守恒方程A-18用来求解各组分摩尔数。
2 聚合物驱的物理模型
正如引言中提到的那样,聚合物驱机理是非常复杂的。EMpower是 ExxonMobil公司在MARS模拟器基础上开发的新型模拟器。其特点包括:用非结构化网格模拟聚合物驱;聚合物溶液性质与矿化度、剪切增稠和聚合物降解等因素有关。该模拟器结合油藏中流体的流动、布井方式、流线和工艺技术,能够准确有效地模拟复杂油藏。
2.1 聚合物溶液黏度
聚合物溶液是非牛顿流体,在低剪切速率下,黏度随剪切速率的增加而降低。但是,一些学者已经证明了聚合物溶液在多孔介质中具有明显的剪切增稠特性。2008年,Delshad等人证明了剪切增稠是德布拉数的函数。EMpower既能模拟聚合物的剪切稀释,又能模拟剪切增稠。除剪切速率外,聚合物溶液黏度还是聚合物浓度、矿化度和温度的函数。
2.2 传导率修正
通常,近井地带的剪切速率高于油藏中的剪切速率。因此,从井底到油藏中剪切速率的变化需要特殊处理,尤其是当井眼位于大网格块中时。在本文的研究过程中,根据近井地带剪切速率的变化对传导率进行修正,这可以通过模拟井眼周围压降对黏度的影响来实现。
2.3 不可入孔隙体积
不可入孔隙体积 (IPV)描述了聚合物不能进入的孔隙空间。IPV可理解为:孔壁排斥效应和孔喉排斥效应。在孔壁排斥效应中,聚合物溶液流经所有孔隙,但聚合物集中在高速区而远离孔隙表面。在孔喉排斥效应中,聚合物只流经大孔隙 (含一部分中孔隙)而不流经小孔隙。在 EMpower中,考虑到IPV的影响,对聚合物的流速进行了调整。IPV与岩石类型和渗透率有关。
2.4 聚合物吸附
吸附和滞留是聚合物在多孔介质中损失的主要原因,与渗透率 (代替孔隙表面积)有关。EMpower可将聚合物吸附分为可逆和不可逆两种情况进行模拟。
2.5 残余阻力系数 (RRF)
聚合物吸附可引起孔隙缩小,从而降低水相渗透率。水相渗透率下降是聚合物吸附量的函数。通常,残余阻力系数只降低水相渗透率,几乎不影响油相渗透率。
2.6 聚合物降解
聚合物不仅会发生热力学降解,还会与地层水中的金属阳离子反应而沉降。不同的油田,对聚合物耐盐性有不同的要求。本文在模拟聚合物降解时考虑了温度和各种金属阳离子的影响。
3 数学方程
模拟时间步的目的是为了获得在该时间步结束时的压力、组分数量及相饱和度,可根据岩石和流体的性质获得这些参数的初始值。文中建立了多个数学方程,通过IMPES、耦合-隐含、顺序及IMPSAT算法来求解这些未知数。在解出压力、饱和度及其他组分的摩尔数之后,再求解聚合物的摩尔数。方程的选择需要综合考虑稳定性和计算机的运算能力。
根据体积守恒方程A-8可推导出求解压力变化的线性方程。线性方程A-15的算法决定了求解组分摩尔流量的复杂程度。
3.1 IMPES算法
对于IMPES和顺序算法,压力方程如式 (1)所示:
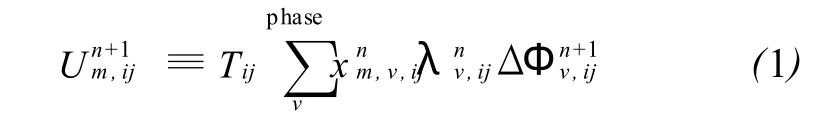
由于其稳定性差使用得较少。在IMPES算法中,压力随时间变化,而饱和度是固定不变的。当流速较高、前缘饱和度变化较快的时候,不能很好地模拟油藏实际情况。
3.2 耦合-隐含算法
1980年,Coats提出了耦合-隐含 (CI)算法,可同时准确求解压力和组分摩尔数。与IMPES算法相比,它更稳定,但运算速度较慢。CI算法的组分流动方程如下所示:
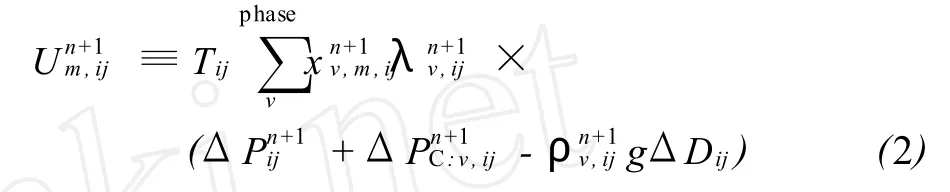
组分的摩尔守恒方程见A-15。对式 (2)相饱和度求导 (因为方程中饱和度是因变量)便可得相体积守恒方程A-7。体积守恒方程A-8用来求解压力。
3.3 顺序算法
1973年,Spillette、Hillestad和Stone提出了一种介于IMPES算法和CI算法之间的顺序算法。1986年,Watts用同样的方法建立了组分模型。与CI算法同时求解压力和摩尔数不同,顺序算法是先求解压力,然后依次求解饱和度和摩尔数。首先,用顺序算法将压力方程线性化以求解压力变化;然后将饱和度方程线性化,求出饱和度变化;再将组分的摩尔守恒方程A-15线性化,便可计算组分数变化;最后,根据最新的组成计算下一时间步的饱和度。
3.4 IMPSAT算法
1989年,Quandalle和Savary首次提出了IMPSAT算法,称之为隐式压力、隐式饱和度算法。1999年,Cao和Aziz在传导方程中显式计算相密度和组分的摩尔分数,研究表明,压力与组分摩尔分数之间的相关度要比压力与相饱和度之间的相关度弱。根据定义,IMPSAT算法同时隐式求解压力和饱和度,而显式求解组分摩尔分数,因此,它相似于但又不同于分两步求解压力和饱和度的顺序算法。在这几种算法中,隐式程度由低到高的顺序为IMPES、顺序、IMPSA T、CI。与之对应,IMPSAT算法在运算上的稳定性比IMPES算法和顺序算法要好,但比CI算法差。因为IMPSA T算法每个节点可以求解3个未知数,所以比IMPES算法 (每个节点求解1个未知数)和顺序算法 (每个节点求解1+2个未知数)的运算成本高,但与全隐式算法相比,对计算机内存和CPU的要求相对较低。
4 聚合物摩尔守恒
为模拟聚合物驱油过程,还需增加聚合物和盐的摩尔守恒方程。式 (3)所列方程包含水相中溶解的聚合物、岩石表面吸附的聚合物、降解损失以及水相中作为示踪剂的聚合物的量。该方程包括黏度和吸附对水相流度的影响以及IPV对聚合物流速的影响。
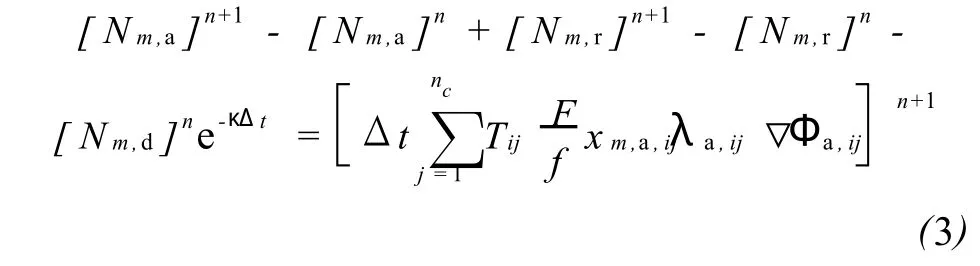
式中 m——聚合物组分;
a——水相;
r——岩石;
d——降解后的聚合物;
κ——热降解常数;
Nm,a——溶解聚合物的摩尔数;
Nm,r——岩石表面吸附的聚合物摩尔数;
Nm,d——降解的聚合物摩尔数;
F——模拟低渗透岩石对聚合物的“封堵”系数;
f——不可入孔隙体积的函数。上式可简化为:
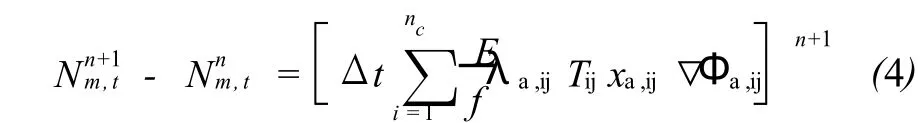
式中,t表示聚合物总摩尔数。在每个网格中,将聚合物吸附和降解看作点源和点汇。显式算法中,在时间步开始时求解这些参数并假设其在时间步长中保持为常数。降解常数κ由用户自定义。先计算降解再计算吸附。吸附是水相中聚合物浓度的函数,并符合Langmuir等温吸附。残余阻力系数是聚合物在岩石表面吸附量的函数,反映了该网格聚合物的吸附量和降低水相渗透率的能力。获得吸附降解后的聚合物浓度,便可计算水相黏度,从而通过方程 A-4可计算相流度。通常,f=1.0-IPV (IPV由用户自定义),并存在区域性变化。F是模拟低渗透岩石对聚合物的“封堵”系数,是网格渗透率的函数。虽然聚合物摩尔数可通过显式或隐式求解,但还是应根据稳定性来决定采用哪种方式求解。假设水相密度不受聚合物浓度的影响。
5 模拟结果
5.1 模拟岩心驱替实验
将EMpower模拟聚合物驱的采收率情况与Masuda等人1992年的岩心驱替实验结果进行比较。Masuda等人测量了 HPAM溶液在玻璃微珠人造多孔介质模型中的流变性 (图1),并通过岩心驱替实验测量了聚合物驱采收率提高幅度。在不调整模型参数的情况下,EMpower模拟结果与实验结果的拟合度较高。实验和模拟结果如图2和图3所示。
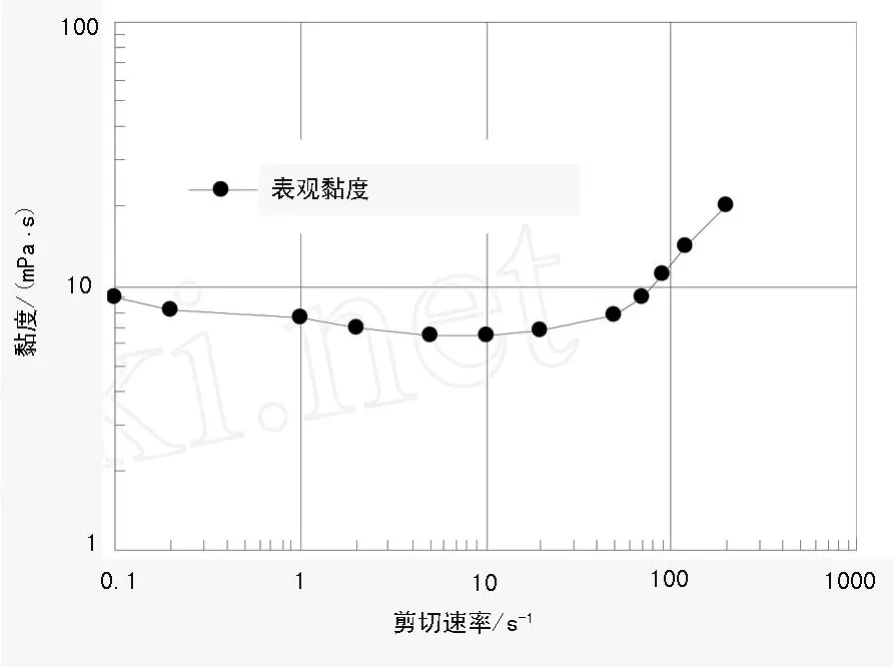
图1 HPAM溶液 (200 ppm)的流变曲线
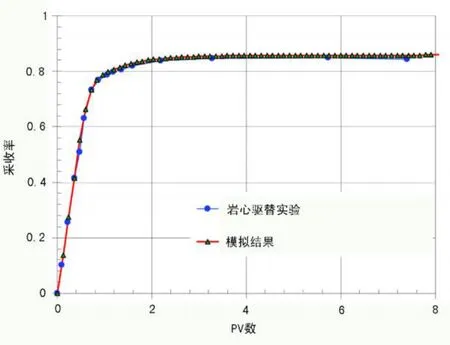
图2 采收率随注入PV数的变化曲线
5.2 非结构化网格模型
2001年,Beckner等人为 ExxonMobil公司开发了非结构化网格模拟器 EMpower。对复杂结构井(如大斜度井、水平井和多分支井)、断层和尖灭进行网格划分是比较复杂的,但使用非结构化网格就比较简单。
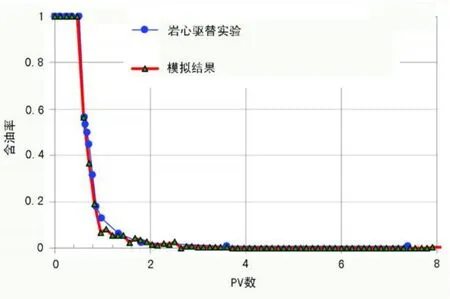
图3 含油率随注入PV数的变化曲线

图4 五点井网非结构化网格示意图
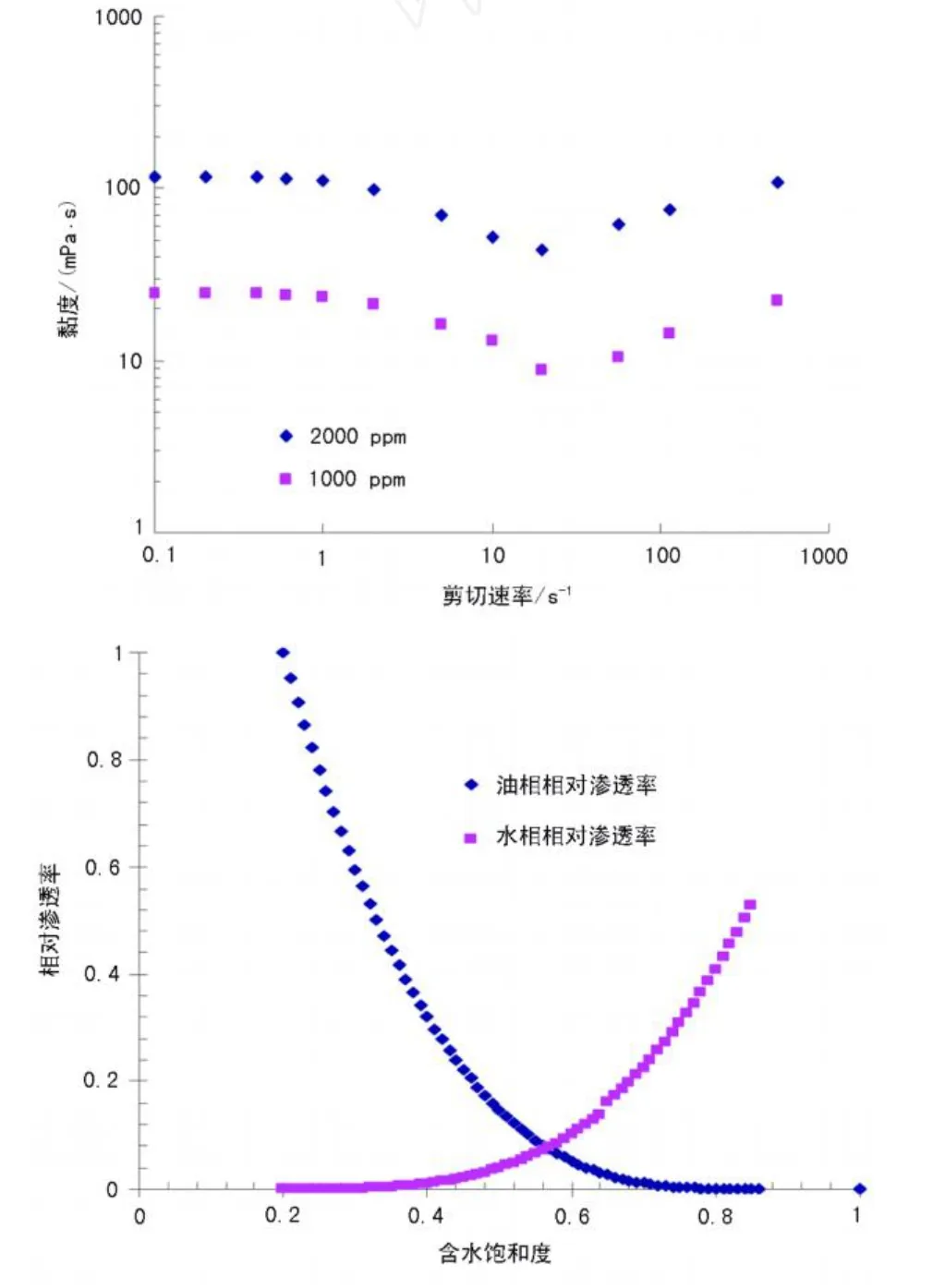
图5 岩石和流体性质
非结构化网格允许使用多种网格技术对五点井网模型进行模拟 (图4)。网格结构对聚合物驱效果影响很大,而非结构化网格就降低了这样的影响。当聚合物溶液黏度低于油相黏度 (如聚合物驱替稠油)或者高黏聚合物驱转后续水驱时,容易发生黏性指进,应特别注意网格的方位敏感性。五点井网模型聚合物驱实例的网格结构如图4(a)所示。模型尺寸为500 ft×50 ft×50 ft(1 ft=30.48 cm)。聚合物溶液的流变性如图5所示。聚合物遵循Langmuir等温吸附,最大吸附量为20μg/g砂。IPV为0.2。水相渗透率下降了20%,但油相渗透率不受影响。模型孔隙度为26%,渗透率为2 D。油水相对渗透率曲线如图5所示。油藏初始含水饱和度为束缚水饱和度,初始压力为2 140 psia(1 psi=6.895 kPa)。为了简化,不考虑矿化度、聚合物降解和油水压缩性的影响 (体积系数为1),并且只模拟二维的情况。聚合物注入浓度为1 500 ppm(1 ppm=10-6),注聚时间为10年。产油井井底压力为1 500 psia。五点井网模型复杂非结构化网格中含油饱和度和聚合物浓度如图6所示。目前已开展针对实际地质模型的模拟,运算速度较快。
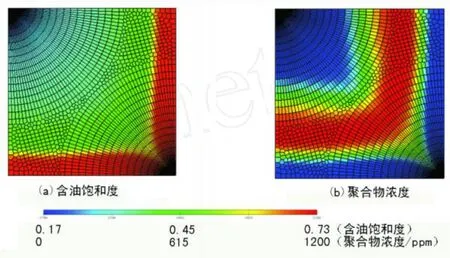
图6 注聚5 730天后的含油饱和度和聚合物浓度分布
6 结论
非结构化网格可以详细地模拟聚合物驱过程,并有效地模拟复杂油藏。
聚合物驱模拟包括聚合物的流动特性和驱替效果,其驱替特征如下:
◇聚合物溶液黏度是聚合物浓度、剪切速率、矿化度和油藏温度的函数;
◇聚合物溶液黏度具有剪切稀释或剪切增稠的特性;
◇传导系数受近井地带高速剪切的影响;
◇聚合物降解是聚合物浓度、离子浓度和油藏温度的函数;
◇聚合物滞留对聚合物流动特性有重要影响;
◇可使用多种数值算法 (如顺序算法,IMPSAT等)和多种模型 (如黑油模型、组分模型和热采模型)进行聚合物驱模拟。
资料来源于美国《SPE 118985》
10.3969/j.issn.1002-641X.2010.7.001
2009-04-08)
