气液两相流管道中的瞬态流动及清管操作模型＊

王荧光 裴红 刘文伟 李研 (中国石油辽河工程有限公司)

气液两相流管道中的瞬态流动及清管操作模型＊

王荧光 裴红 刘文伟 李研 (中国石油辽河工程有限公司)

对于气液两相流的瞬态模拟,需要对连续性方程、能量方程及动量方程进行复杂的计算。简化的瞬态清管模型是采用近似的稳态假设和某一流态下两相局部动量平衡的方法,对连续性方程和动量方程进行适当的简化。TACITE瞬态清管模型是以漂移流动模型的数值分辨率为基础,可用于多相传输中遇到的有关坡度、流动特性和流动状态的任何情况,其精确的数值格式可以对混合物组成进行精确的追踪。通过将模拟结果与实测数据进行对比表明:这两种模型的模拟结果均可满足工程需要,TACITE模型模拟数据与实测数据具有更好的一致性。

瞬态流动 瞬态模拟 清管段塞流 两相流

在两相流集输管道中,最重要的瞬态条件是入口流体流率的波动、出口压力的变化和清管过程。定期对集输管道进行清管操作可以清除管道内的积液。为了使管道设计更加便捷和安全,对瞬态操作进行模拟和分析是十分必要的。对流体质量守恒方程、动量守恒方程和能量守恒方程的顺利求解能够预测管道内的瞬态水力特性。为了减少计算机编程的复杂性,可对上述提及的平衡方程进行简化以得到一套实用的程序。Taitel、Shoham和Brill(1989)将气体近似的稳态假设和两相局部动量平衡相结合,提出了简化的瞬态模拟模型。Minami和Shoham (1994)提出了新的预测流态的方法,并将其与实验数据相对比后对上述模型进行了修正。Mc-Donald和Baker(1964)是最早对两相流管道中的清管过程进行研究的学者。Barua(1982)进一步完善了McDonald和Baker的清管模型并移除了主模型中的一些限制性假设。Kohda(1988)根据漂移流模型提出了第一个基于完全两相瞬态公式化的清管模型。Minami和Shoham(1991)将清管模型与Taitel(1989)提出的简化瞬态模拟器整合到了一起。现采用简化的瞬态清管模型和 TACITE瞬态清管模型模拟清管器的运动。

1 简化的瞬态模型及清管模型[1]

1.1 简化的瞬态模型

对于气体,将应用近似的稳态假设。气体的连续性方程为mg=ρgQg=ρgVgAg;液体的连续性方程为

◇分层流

在分层流中,具有局部平衡假设的两相流动量方程为:

◇环状流

该区域与分层流相似,当气体没有湿润管壁时(Cwg=0),分层流的方程对于环状流同样有效。

◇泡状流或雾状流

对于这两个区域,假设在气相和液相之间没有滑移,则均相模型可以使用。混合液动态方程为

◇段塞流 (图1)

段塞流可分成两个区域:分散泡状流和分层流。对于段塞流,可以推导出预测段塞速率的最后方程为。为了计算段塞速率,应该确定段塞内的液体持液率。通过Gregory关联式段塞流内的平均压力梯度可以确定为:此处注意Vlf的正方向是上游方向。剪切系数可表示为C=f S/2A,段塞流的雷诺数小于2 000,摩擦因子为64/Re。在分层流中,根据Cohen和Hanratty(1968)的研究数据,此处摩擦因子为0.014。在环状流中摩擦因子可通过Wallis(1969)关联式得出:。确定一个判定管道中流态的标准是十分必要的,计算程序可以以该标准来判断管道内的流体状态。如果流态改变了,则连续性方程和动量方程的求解方法也随之改变。流态的预测已被 Taitel和Dukler(1976)、Taitel(1980)、Barnea(1986)、Minami(1991)描述过。现采用Minami(1991)提出的段塞不稳定性方法。提及的方程可表述为(ρlElsALs)+ρ(Vl-Vt)ElA +ρl(0-Vp)(1-E)(-A)=0,液体段塞长度随时间的变化可根据平移速率和清管器速率的差表述出来,因此可得到平移速率为Vt。段塞中的液体持液量可由Gregory公式得到,段塞速率(Vss)可通过清管器上游和下游之间的质量平衡得到如下公式ρlVss(Vt-Vp)ElsA+ρlVl(Vl-Vt)ElA=(Pp-Pf)A-ρsgA(Zf-Zp)-τsπdLs,通过该方程可以求得液体段塞部分的总压降。

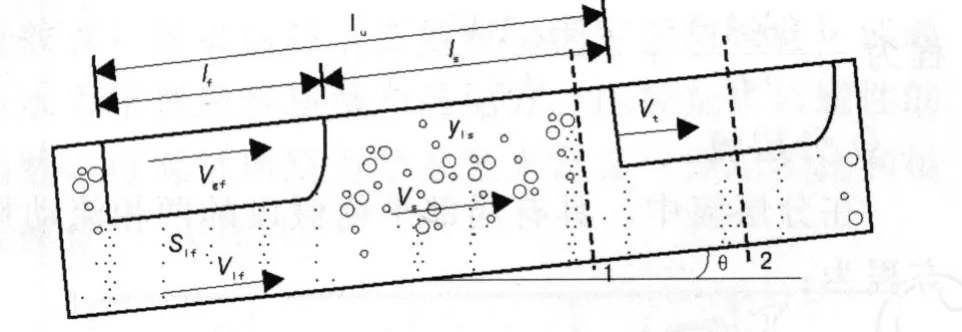
图1 段塞的结构

1.2 清管模型

研究中采用的清管模型是以Minami(1991)的研究为基础的[1]。根据该模型管道被分成三个区域。①上游瞬态两相流区;②段塞区;③下游瞬态两相流区 (图2)。为了模拟清管器在管道中的运动,移动坐标中的质量守恒和动量守恒被应用在段塞流区域内。对于运动控制体和扩大控制体,以上

图2 清管模型

1.3 数值求解

为了对简化瞬态模型进行求解,采用半隐式有限差分方式将连续性方程和动量方程离散化。同时应用对气体和液体的连续性方程采用向后差分逼近,对压力方程采用向前差分逼近的矩形网格系统。为了模拟清管期间和清管后的瞬态行为,需要将清管模型与早期描述的瞬态模型耦合到一起。清管器被假设成一个在移动的边界条件,气体不允许通过该边界,部分液体可以滑移通过该边界。段塞前部也是一个移动的边界。一般清管器的速率与清管器后部的气体速率相同,故可通过清管器的速率计算每一时间步的清管器的位置。段塞前部的新位置也可通过清管器的平移速率计算得到。计算得到清管器和段塞前部的位置后,可以将简化的瞬态模型应用到下游瞬态区域来确定压力。边界条件是管道出口的压力和入口的流率,压力和流率可通过下游两相流截面和液体段塞部分截面之间应用质量守恒得到。气体的关联式为(1-Els)(Vt-Vs)=(1-El)(Vt-Vg),因此,通过该方程得到的气体速率可计算得到气体的流率。采取同样的方式可得到液体流率。下游流体区域得到求解后,便可以通过该方程得到液体段塞部分的压降。这样加上清管器的压降便可以得到清管器上游的压力。清管器的压降可通过 Kohda、Suzukawa和 Furukawa(1988)提出的经验关联式计算得到。对于上游流体区域,可采用另外一维简化瞬态模型进行计算,该模型给定了气体和液体的入口流率及清管器处的压力作为出口边界条件。

2 TACITE瞬态模型及清管模型

2.1 TACITE流体动力学模型[2]

TACITE模型是一种漂移流动模型,该模型分解了4个守恒联立方程:质量守恒方程、能量守恒方程、动量守恒方程和热力学闭合方程。TACITE通过一个取决于流动状态稳态闭合关系的曲线来恢复有关相间滑脱的遗漏信息。为了确定相态,假设每种状态都是两个基本方式的空间与时间的结合:分离流动 (层状流和环状流)和分散流动。这样间歇流动便可以看作是这两个基本方式的结合,并且通过分离流的比率β(分散流β=0,分离流β=1,间歇流0＜β＜1)来确保闭合规律的连续性。因此,该模型的独创性就在于:动力方程组确保了模型在整个流动状态转换期间的连续性;闭合定律对坡度和流体特性来说保持了其连续性;在计算变量连续性的基础上建立了流态的转换理论。

2.2 TACITE流体热力学模型[2]

TACITE含有最优化的完整的热力学闪蒸,可保证给定组分的相性质和相平衡计算的可靠性。该闪蒸算式使油-气-水三相平衡计算更加准确。TACITE计算时间会随着跟踪组分数量的增加而增加,因此计算时实际上不是以定义的实际组分来进行模拟,而是首先将流体组分分成N个虚拟组分,再估计虚拟组分的性质。最后在适当的温度压力范围内将虚拟组分的性质加以优化,用虚拟组分的性质来替代初始组分的多种性质,这样可以减少组分的数量,保证流体性质模拟的准确性。设定的虚拟组分最佳分馏界限应使蒸汽质量分数或状态参数方程的目标函数最小化,这种方法是首次在TACITE中加以应用的。该二进位表示法对于标准流体模拟是十分准确的。

2.3 TACITE流体的热传递模拟[2]

TACITE编码具有四种热传递模拟方法:①使用自己定义的流体温度梯度;②采用稳态计算得到的温度梯度;③瞬时热传递,即假设在特定的位置径向热传递速率比连续稳态径向温度场的传递速率快;④包括各层间惯性的瞬时热传递,即假定由于管道及保温材料的热容量的有限性使径向热传递比瞬时温度场的热传递速度快。

2.4 TACITE的数值格式[2]该数值格式所采用的守恒方程为=S。该方程是一个非线性双曲型组,可使迭代循环中和沿管线单元有较好的质量和能量平衡,同时该方程也是非耗散型的,可以确保有较好的正面跟踪能力,可较准确地应用到段塞流的模拟。在段塞流发生时孔隙率波会向两个方向扩展,这样采用显隐式混合格式来优化计算速度和正面跟踪能力对段塞流的预测便显得十分重要。

2.5 TACITE清管模型[3]

TACITE编码中清管模型对清管过程中的质量守恒充分考虑了管线泄漏影响,并对清管器前部堆积液体量进行预测;清管过程中的力平衡考虑了清管器两侧压力损失和使清管速度降低的壁面阻力的影响。可设定发球位置和接收位置、清管器的长度和质量,以及壁面摩擦因子。

3 结果与讨论

3.1 简化的瞬态模型及清管模型的验证[1]

为了验证模型的有效性,将简化的瞬态清管模拟计算结果与Minami(1991)所收集的试验站数据进行比较。首先,对直径80 mm、长420 m的管道进行稳态计算。该管道入口液体流率是0.004 m3/s,气体流率是0.085 m3/s,出口压力是183 kPa。清管器在t=66 s时装入发球桶中。在清管操作前所得到的流体状态是分层流。图3显示出了分别位于管道入口64 m和203 m处的两个测量站内压力的变化。将清管器放入发球桶后由于清管器下游流率的降低导致了压力的下降。当段塞前部到达1站时,压力急剧增加直到清管器通过1站;同时液体段塞长度的增加也导致了压力的显著增加。当段塞进入分离器后,所有测量站的压力迅速下降。

图3 1站和2站处的压力变化

可以看到,在清管前后的稳态流动中,压力预测值和实测值间具有一定的差别,这表明所使用的稳态计算模型由于具有前面所提及的简化假设使其不是非常准确。所预测的清管器到达收球桶的时间比实际测量时间要短,这表明所预测的清管器速率要比实测的速率要高。这主要是由于模型中进行了不允许任何气体通过清管器的假设,然而众所周知,实际上气体是可以通过清管器与管壁间的间隙的。在预测速率与实测速率之间的差异也导致了清管器运动期间预测的压降要比实际测量的压降要大。

图4显示出了1站液体持液率的变化。所预测的液体持液率的变化与实际观察值很接近,但在段塞区域持液率的预测存在一定的误差,这是由于Gregory关联式的不准确造成的。在清管器上游和与稳态模型持液率计算相关的段塞区域下游处的持液率的预测也存在微小的误差。图5显示出了清管期间及清管后管道内液体持液率的分布。可以看到,清管期间在清管器的后部有一气体区域,并且在管道入口附近将形成两相流。同时可以看到,清管后将发生液体重新恢复的现象。

3.2 TACITE瞬态模型及清管模型的验证[3]

将TACITE动态清管模拟计算结果与 MIRANDA(1996)数据库所收集的Bekapai油田数据进行比较 (图6)。该数据来自于长42 km的集输管线,管线内充满黏度为1 mPa·s的油品。通过数据对比发现,清管过程中压力、持液率等参数与简化的瞬态清管模型具有相同的变化趋势。模拟中清管器到达收球桶的时间大约为13 000 s,比数据库中的时间早了大约600 s。预测的入口压力与数据库数据相比要稍高些,但在清管器收球处的压力和数据库数据几乎一样。从出口液体持液率上来看,预测值和实际数据有很好的一致性。对于出口气体流率,在清管前、清管后和清管期间预测值与实测数据也具有很好的一致性。由于数据库没有收球桶孔板抬起期间的数据,故无法对该阶段进行比较。因此,程序计算得出的液体流率较高,为18 kg/s。

图6 TACITE模型模拟数据与实测数据对比

4 结论

简单瞬态清管模型模拟结果与Minami(1991)得到的试验站数据的比较表明,除了在段塞内的液体持液率和清管速率由于不允许气体通过清管器的假设造成的微小差异外,该模型对清管器及段塞等参数的模拟还是比较准确的。上面所提及的微小差异对于实际工程计算和设计来说是安全的,从该角度看此模型还是十分成功的。

TACITE瞬态清管模型所模拟的数据具有较好的重复性,且与数据库数据具有很好的一致性,这主要是由于TACITE模型具有准确的数值格式。此外,TACITE编码中清管模型对清管过程中的质量守恒充分考虑了管线泄漏影响和清管过程中的力平衡,因此 TACITE瞬态模型及清管模型具有较大的优势。TACITE瞬态模型的准确性已得到AGIP、TOTAL和ELF的验证,特别是通球模型在油气集输领域的有效性也得到了验证[4]。目前TACITE瞬态模型及清管模型已商业化,并成功地应用于工程设计[5]。

符号说明

mg、Qs——气体的质量流率、体积流率

Vg、Vl——气体速率、液体速率

ρs、ρl——气体密度、液体密度

Ag、Al——分别为气体、液体占据的截面积

yl——液体持液率

Cwg、Cwl、Ci——分别为气体、液体、表面剪切系数

θ——管道的倾斜角

fm——摩擦因子

ρm——密度

Vm——混合流体的速率

D——管道直径

Vs——段塞流速率

Vlf——膜区域液体速率

ls——段塞长度

lf——膜区域长度

l——一个段塞单元的总长度

yls、ylf——分别为与段塞、膜区域相关的液体持液率

Vd——漂移速度

C——通过试验确定的(文中C取1.2)

fs——摩擦因子

ρs——段塞区域的密度

S——管道的周长

A——管道横截面积

f——通过Hall方程得出的摩擦因子

Dh——水力直径

Re——雷诺数

ε——环状流的环厚度

Els——液体段塞中的液体持液量

E——清管效率或清管器航道后部的含气率

Vp——清管器速率

Vl——段塞前部下游的液体速率

El——段塞前部下游的持液量

Pp——清管器处的压力

Pf——段塞前部的压力

Zp——清管器所在位置管道的高程

Zf——段塞前部所在位置管道的高程

τs——段塞区域平均剪切力

Ls——清管器前部段塞的长度

W——守恒变量

F——流量

S——源项

[1]Hosseinalipour S M,Salimi1 A,Khalili A Zarif.Transient flow and pigging operation in gas-liquid two phase pipelines[J].16th Australasian Fluid Mechanics ConferenceCrown Plaza,Gold Coast,Australia, 2007:976-979.

[2]Pauchon C D,Hulesia H,Lopez D,et a1.TACITE:a comprehensive mechanistic model for two-phase flow [R].Cannes:presented at the 6th BHRG Multiphase International Conference,1993.

[3]Coadou L,Duchet-Suchaux P,Ferre D et a1.Pigging operation:measurement and simulation[C].Multiphase 99:1-12.

[4]DuretE,Lebreton E,Heintze,et al.Pipeline bundles model implemented into a multiphase flow model[R]: SPE 62948,2000.

[5]王荧光.苏里格气田集输管线清管过程瞬态模拟[J].天然气工业,2009,29(11):94-99.

10.3969/j.issn.1002-641X.2010.10.013

2009-11-16)

＊本文受到国家科技重大专项项目“煤层气田地面集输工艺及监测技术”(编号:2009ZX05039)的资助。