中国足球超级联赛动态竞争平衡分析
2010-09-30张宝钰
张宝钰,张 林,王 岩
(上海体育学院赛事研究中心,上海200438)
中国足球超级联赛动态竞争平衡分析
张宝钰,张 林,王 岩
(上海体育学院赛事研究中心,上海200438)
主要采用文献资料法和数理统计法,从动态的视角对中国足球超级联赛竞争平衡进行分析。发现中国足球超级联赛动态竞争平衡波动较大,动态竞争平衡稳定性较差,但动态竞争平衡水平有提高的趋势。
中国足球超级联赛;动态竞争平衡;肯德尔等级相关系数
本研究从联赛动态竞争平衡的视角,分析中国足球超级联赛(以下简称中超)球队赛季排名发生变化的动态竞争平衡情况。对职业体育联赛竞争平衡的衡量可以分为静态和动态两大类。静态竞争平衡主要是关注单赛季竞争平衡情况,对竞争平衡的衡量是相对的静止状态,所以称作静态竞争平衡;而动态竞争平衡的衡量是对赛季之间排名的变化情况进行动态的分析,是一种相对连续的状态,所以称为动态竞争平衡。动态竞争平衡更关注球队本身的特质,对相邻赛季所有球队排名发生变化的情况进行衡量。从静态的角度分析联赛竞争平衡,竞争可能是平衡的;如果从动态的角度分析,竞争可能是不平衡的。如果赛季之间的排名完全相同,从静态的角度看竞争可能是平衡的,而动态角度竞争是完全不平衡的,动态是考虑赛季之间的排名变化情况,是对相邻赛季竞争平衡的衡量,对竞争平衡水平衡量具有一定的连续性。由于静态是单赛季的衡量,而动态是相邻赛季的衡量,包括多个赛季的竞争平衡情况。联赛的动态与静态竞争平衡有一定的区别。衡量球队动态竞争平衡常用的方法主要是一定时期球队进入前几名的累积百分比(Top k)[1];还有赫氏指数(HH I)[2],反映球队分享冠军的集中程度。用Top k和HH I衡量动态竞争平衡存在一定的局限性,这两个指标只关注排名靠前的球队位置的变化,而没有关注联赛全部球队排名的变化情况,缺乏全面性。为此本研究拟采用一种相对比较全面衡量联赛动态竞争平衡的方法——肯德尔等级相关系数法(kendall’s rank correlation coefficient tau),对中超动态竞争平衡情况进行分析。肯德尔相关系数法能够衡量相邻赛季所有球队排名变化的情况,相对以上衡量动态竞争平衡的方法而言是一种全面的方法。
1 职业体育联赛动态竞争平衡
动态竞争平衡指的是球队在两个相邻赛季排名发生变化的相关程度。在理论上讲应该是一种动态完全竞争平衡状态。动态完全竞争平衡是完全的负等级相关,在每两个相邻的赛季一些球队都有机会获得一次冠军,在两个相邻的赛季一支球队有机会获得两次亚军,以此类推情况相似,当然必须是两个相邻的赛季排名发生最大化改变,但是3个赛季为零的情况。因此动态完全竞争平衡的描述是两个相邻的赛季排名完全独立存在,也就是动态完全竞争平衡,每个赛季的排名出现的情况都是相似的,上赛季的排名对本赛季的排名没有影响,当然这种情况非常少见,这只是在理论上对完全动态竞争平衡的分析。但是由于足球联赛一般存在升降级制度,不会出现这样的情况。动态竞争平衡更关注联赛所有球队相邻赛季排名发生变化的情况,但是必须强调的是静态与动态竞争平衡是各自独立的,两者可能是相反的方向。在现实中对动态竞争平衡的界定是一种相对的平衡状态,对于中超赛制而言完全的竞争平衡状态基本不会出现。
从理论上推测一个完全竞争平衡的比赛就是比赛结果不可预测性;一个完全不平衡的比赛意味着在比赛之前已经知道比赛的结果,强队永远战胜弱队,比赛没有任何悬念而言。对于职业体育联赛竞争平衡有不同的表述,比如比赛的不确定性、赛季的不确定性、冠军的不确定性,以及升降级的不确定性,这些研究主要是对具体某一场比赛或一个特定的赛季比赛结果的不确定性,对于赛季之间比赛的竞争平衡问题没有涉及,是一种相对孤立的状态,对于球队赛季之间排名变化缺乏联系,基本还是一种相对静态的竞争平衡分析。对于竞争平衡的研究从动态的角度进行分析是一种相对更为合理、全面的视角。动态竞争平衡更多关注球队在相邻赛季之间排名变化情况,这种对竞争平衡的衡量可以对一个职业体育联赛竞争平衡情况更为深入、全面的考察。对动态竞争平衡的概念了解之后,接下来以对数据的选择与衡量方法进行说明。
2 动态竞争平衡衡量方法的选择
2.1 肯德尔等级相关系数法
本研究主要资料是中超历年的最终排名数据,采用肯德尔等级相关系数法对中超动态竞争平衡情况进行分析。对于联赛球队在相邻赛季的排名变化相关性的分析,通常采用二元定序变量的相关分析。二元定序变量统计学上的定义为有序变量或顺序变量,它取值的大小可以反映观察对象的某种顺序关系(等级、方向和大小等等),也就是基于“质性”因素的变量。关于相关性的检验主要包括两种方法:斯皮尔曼(Spear man)和肯德尔(Kendall’s tub)等级相关系数衡量定序变量之间的线性关系,利用的是非参数检验方法[3]。斯皮尔曼等级相关只可以用于以等距或定比等级测量的资料;肯德尔等级相关用于定序等级的资料,肯德尔相关系数用τ表示,是统计学中一个常用的系数,用来描述两个序列的相关系数,可以用来比较两个序列的相似性,如果两个序列完全一致,则肯德尔相关系数τ=1,两个毫不相关的序列的肯德尔τ=0,而两个互逆的序列的肯德尔τ=-1[4]。联赛相邻赛季的排名数据资料适合采用肯德尔等级相关系数法,所以本研究采用肯德尔等级相关系数衡量联赛的动态竞争平衡是一个科学合理的方法。应用肯德尔等级相关系数法有两个优点:一是应用spss统计软件数据便于计算;二是可以通过P值检验值是否具有区别于零的显著性差异,说明一定时期内联赛动态竞争平衡情况。
采用肯德尔等级相关系数衡量球队排名变化的等级,可能在理论上面临两种问题:一种是动态完全竞争平衡的情况,就是球队相邻赛季排名完全不相关;另一种是相邻赛季动态完全竞争不平衡情况,也就是球队相邻赛季排名完全一致的情况。一般来说这种情况是不会出现的,因为足球联赛一般是升降级的制度,升级球队代替降级球队的位置,如果没有升降级的时候在理论上是可能的。当然这只是两种动态平衡极端状态,现实中多数动态竞争平衡是出于这两种的中间状态。下面对肯德尔等级相关系数统计原理进行说明。
2.2 肯德尔等级相关系数法的统计学原理
在统计学上应用相邻赛季排名数值计算肯德尔系数,它的前提必须是相邻赛季球队数相同。下面以两个球队(上海申花和北京国安)相邻赛季的排名变化情况进行说明。第一个赛季上海申花排名a,北京国安b;第二个赛季上海申花c,北京国安d。如果这两个球队的相邻赛季排名位置高低顺序是一致的,也就是a<b和c<d或a>b和c>d,那么具有一致性,相反则具有相异性。如果比较相邻两个赛季的球队排名,如果有N个球队,必须对比所有球队的可能出现的组合情况是,也就是相邻赛季球队排名位置发生最大的移动,然后检验它们是否具有一致性。如果赛季较多,计算肯德尔等级相关系数τ值是一件繁重的工作。本研究将采用一种相对简便的方法,对τ值的计算相对简单,就是利用球队在相邻赛季排名变化的不一致数,这个数有可能是正数或负数,这样就简单了许多。当然应用球队相邻赛季排名移动的最小数与最大数比较,就可以计算肯德尔相关系数τ,最大变化数可以是正常排名顺序(1,2,3……N)或倒序(N,N-1,……2,1),如果移动的一致数用P表示,不一致数Q表示,S代表最大数与最小数之差,那么肯德尔相关系数公式如下(1);由于S=P-Q,并且P+Q=1/2N(N-1),那么肯德尔相关系数公式就是(2);肯德尔相关系数也可以用球队移动的最小数与最大数计算,如果移动的最小数用小Smin表示,移动的最大数用Smax,那么,肯德尔相关系数就是公式(3)[5]。
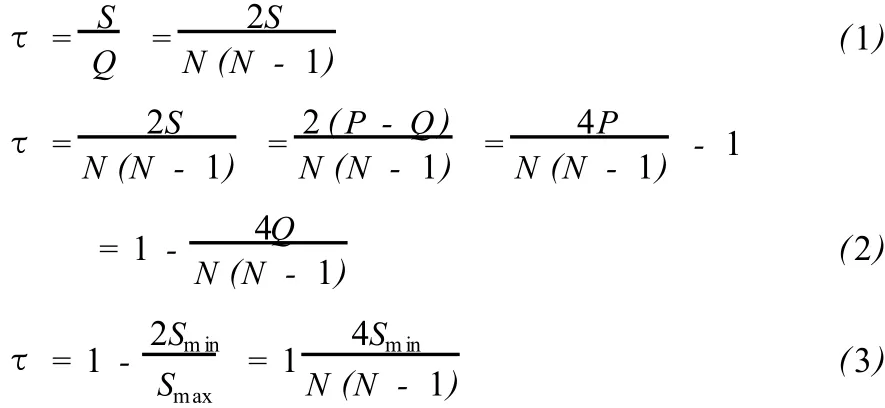
从公式(3)可以知道,如果球队两个赛季排名一样,那么s=0,τ=1,由于排名完全没有变化,从动态看竞争平衡完全不平衡,球队排名没发生变化;如果所有的球队排名都没有变化,那么就是正相关;如果Smin=Smax,那么τ=-1,排名正好是完全相反的方向,这种情况下是完全的负相关;因此可以说τ值在[-1,1]之间。一个动态完全竞争平衡就是相邻赛季所有球队排名都发生变化,这样τ=0。在动态竞争平衡完全负相关时,在3个相邻的赛季中,第1赛季和第3赛季的排名完全一致,第2个赛季排名正好是第1个赛季排名的倒序。综上所述,如果从动态竞争平衡的角度讲,联盟不希望联赛处于完全竞争平衡负相关的情况,因为这样可以预测相邻赛季的最终排名,联赛竞争缺乏悬念。这部分是对动态竞争平衡衡量方法的统计学原理的说明,接下来对动态竞争平衡的衡量过程进行解释。
3 动态竞争平衡衡量过程
3.1 相邻赛季排名变化情况说明
本研究对中超时间界定包括1994—2004赛季的甲A和2004—2009赛季的中超联赛两个阶段。由于中超的前身是中国足球甲A联赛,两个联赛只是在名称上发生了改变,联赛球队的竞技水平基本相同,所以对中超动态竞争平衡的衡量数据从1994年的甲A联赛算起。1994—2004年甲A共10个赛季,2004—2009年中超共5个赛季,总共15个赛季,衡量数据是15个赛季的最终排名。联赛赛季排名是一组时间序列——截面数据(Panel Data),是截面数据与时间序列数据综合起来的一种数据类型,包括时间序列和截面两个维度。中超赛季排名是截面数据,某一球队不同赛季排名是时间序列数据。下面以中超1998—2000赛季数据对肯德尔等级相关系数的计算过程说明,表1是中超1998—2000赛季最终排名情况,表2是Q和P值的计算过程说明。
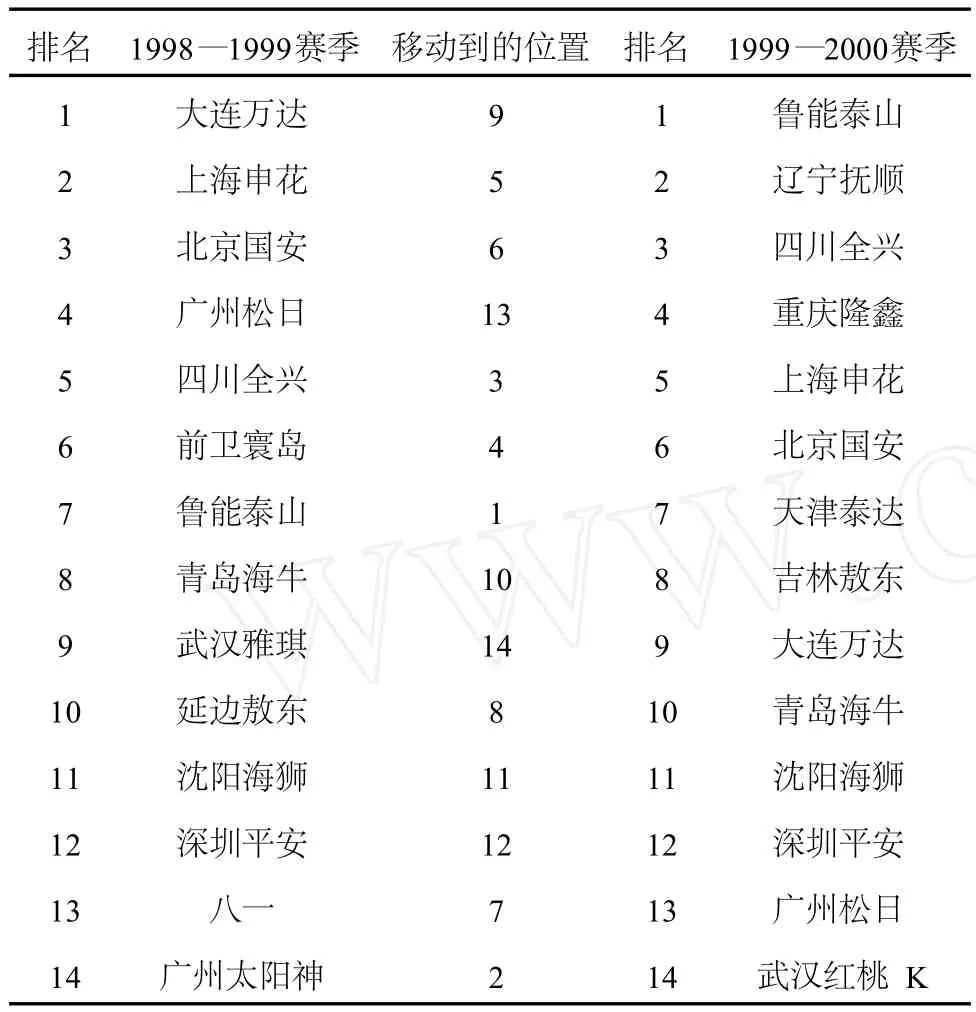
表1 中国足球超级联赛1998—2000赛季最终排名情况
3.2 一致P(不一致Q)数的推算方法(表2)
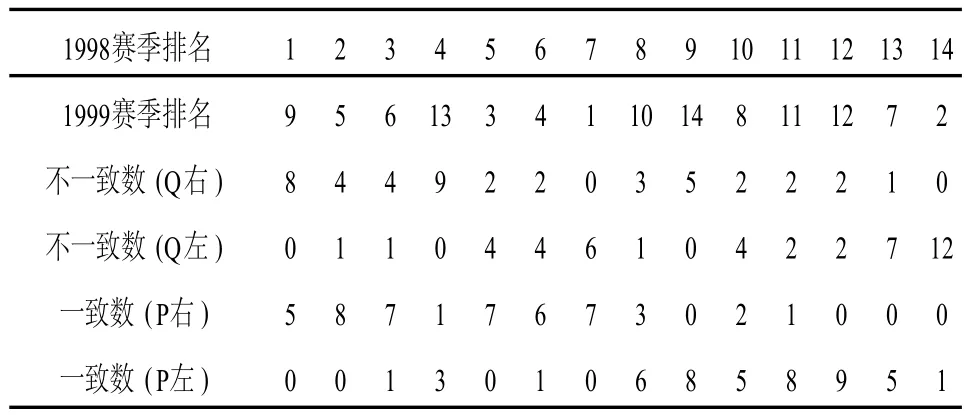
表2 中超1998-1999赛季排名变化情况
不一致数(Q)值的计算要看第二个赛季(第二行)的球队排名变化情况。不一致数(Q右)的计算是观察每个球队本赛季排名的右面(后面)还有几个球队排名在上个赛季高于它的排名,这些球队数相加就是Q值;不一致数(左)的计算方法正好相反,不一致数(Q左)的计算是观察每个球队本赛季排名的左面(前面)还有几个球队上个赛季排名低于它的排名,Q值是所有不一致数之和,并且左右不一致数相等。表2中还说明了一致数(P右、P左)的计算过程,一致数的计算方法与不一致数的计算方法正好相反。一致数(右)的计算是观察每个球队本赛季排名的右面(后面)还有几个球队排名在上个赛季低于它的排名,这些球队数相加就是P值;一致数(P左)的计算方法正好相反,一致数(P左)的计算是观察每个球队本赛季排名的左面(前面)还有几个球队上个赛季排名高于它的排名,P值是所有一致数之和,并且左右一致数相等。其实这种等级对比的实质就是本赛季的排名位置与上个赛季的比较,观察本赛季每个球队排名与上个赛季排名发生变化的整体情况。比如1999—2000赛季的第3名在上个赛季是第6名,在它的后面还有4个球队的排名在上个赛季高于它,这样要求移动的数就是4,Q值是这些所有移动数之和;P值与Q值计算方法相似。应用值的计算公式可以计算出相邻赛季的肯德尔相关系数的值,通过相关系数的值可以判断出等级相关程度。当然我们可以应用公式(4)或(5)两种方法计算肯德尔相关系数值。具体过程如下:
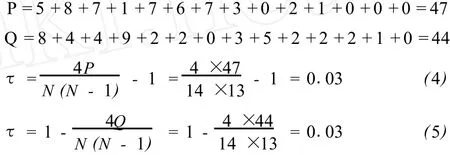
3.3 统计学显著性检验
但是还必须检验参数τ值是否具有区别于零的显著性差异。在理论上可能出现零等级相关,也就是完全动态竞争平衡的情况,即τ=0。想知道是否可以拒绝原假设τ=0,只要观察值τ>0就说明相邻赛季排名独立性越强,也就拒绝了τ=0的情况。利用SPSS计算出的肯德尔相关系数都大于零,说明中超相邻赛季排名相互独立,这样可以拒绝零假设(τ=0),接受备择假设(τ>0)。
可以通过p值判断观察值τ是否具有区别于零的显著性差异,P>0.05的赛季有6个,P<0.05的赛季有9个。当P<0.05时的τ值具有显著性差异,球队相邻赛季排名相关性较强;P>0.05时的τ值差异不显著,球队相邻赛季排名相关性不强。对于中超联赛动态竞争平衡的衡量正好是相反的视角,相关性不强动态竞争平衡较好,相关性强动态竞争平衡反而不好,所以中超动态竞争平衡相对较好的赛季是9个,6个赛季动态竞争平衡相对较差。
3.4 球队的升降级与肯德尔等级相关系数的计算
必须注意赛季球队的升降级情况。中超升降级情况比较混乱。肯德尔等级相关系数的计算必须是相邻赛季之间排名的变化的等级情况,相邻赛季必须保持球队数量相同,但我国中超联赛出现了一些例外的情况,比如球队的解散、合并、赌球降级等问题。特别是球队的合并直接影响到排名的对应问题,球队的数量变化频率较快,这样影响到肯德尔等级相关系数计算。为此对中超相邻赛季球队数进行合理的处理。对相邻赛季球队数相同的处理一般情况下采用升级球队代替降级球队,在个别赛季由于升降球队数不同会造成相邻赛季球队数不一致的现象,以相邻赛季后一个赛季的球队数为准,将球队数保持一致;如果个别球队解散或合并,本赛季的名次用排名靠后的球队依次代替,这样就可以保证相邻赛季球队数相同。中超15个赛季中球队在12~16之间变动,球队数量的变化可能影响整个时期的比较,但是由于球队变化的数量非常小,基本不影响肯德尔相关系数的计算。由于中超特殊的情况造成升降级球队数量相同,说明中超联赛稳定性较差,在英超的历史上还没有出现过升降级不同的情况。中超球队升降级情况见表3。
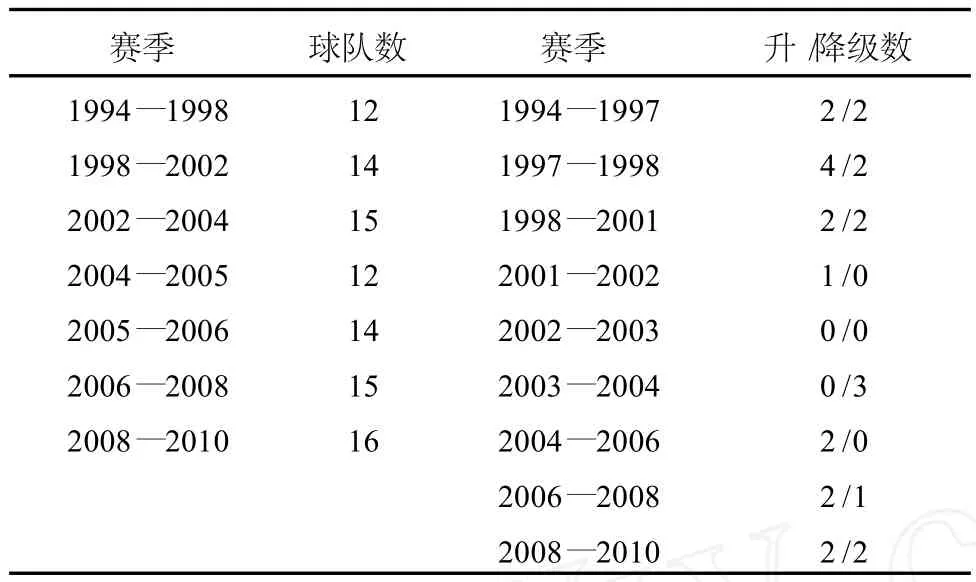
表3 中超球队数与升降级情况
在中超全部赛季中球队数量多数保持偶数,但是在2002—2004赛季和2006—2008赛季为15支球队,出现了奇数。每一轮出现轮空,联赛关键时刻容易出现打假球的现象,所以应避免出现奇数数量的球队数。在中超15个赛季中出现了四个赛季奇数球队数,但是在英超100多年的历史上从来没有出现过奇数球队数的赛季。
以上两部分只是了解了肯德尔等级相关系数计算的统计学原理,以及结合中超赛季排名进行具体说明,肯德尔相关系数的计算是通过SPSS软件进行分析。在对衡量动态竞争平衡方法了解的基础上,接下来对中超动态竞争平衡情况,以及影响中超竞争平衡可能的因素进行初步的分析。
4 中超动态竞争平衡情况的分析
从图1可以看到中超动态竞争平衡的整体情况,更为直观地了解过去赛季动态竞争平衡变化情况,然后采用SPSS软件进行回归分析,对中超动态竞争平衡趋势进行预测。从肯德尔相关系数曲线图可以发现中超动态竞争平衡波动较大,但整体动态竞争平衡水平有提高的趋势。动态竞争平衡水平有一定的改善。总体来说中超动态竞争平衡有以下几个特征。
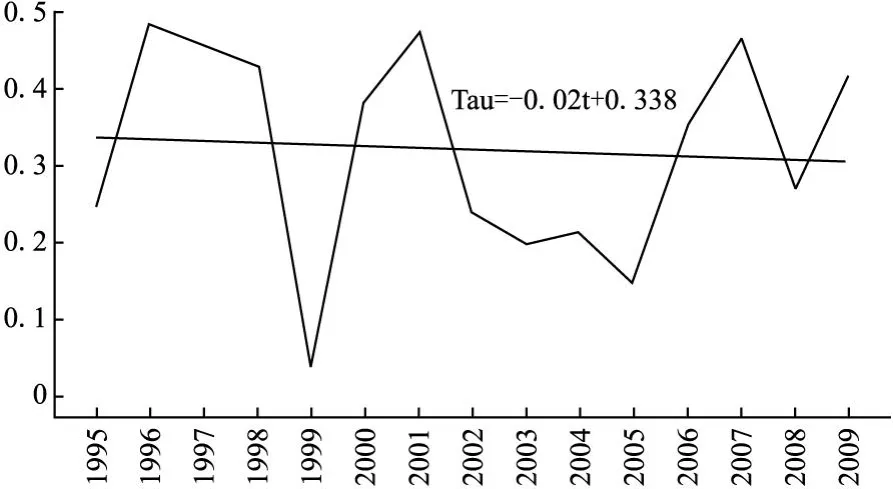
图1 中超动态竞争平衡变化曲线与竞争平衡趋势图
4.1 甲A开始与结束赛季的动态竞争平衡水平基本相当,动态竞争平衡水平相对较好
我国最高水平的足球联赛开始于1994年的甲A联赛,进行了10个赛季,于2004年更名为中超。1995与2004赛季肯德尔等级相关系数分别为0.242和0.212,动态竞争平衡基本相当。甲A联赛十年动态竞争平衡波动较大,基本呈现M型,动态竞争平衡差距较大。动态竞争平衡水平最好的是1999赛季,肯德尔相关系数是0.033,在中超的整个联赛动态竞争平衡水平也是处于最好时期,而1998赛季肯德尔相关系数为0.429,是1999赛季的的13倍,动态竞争平衡水平直线下降,出现了巨大差距。从联赛的竞争平衡来说应该是一件幸事,但短短的一个赛季出现如此之大的差距是不正常的,这种情况的出现应该有其深层次的原因。比如1999赛季渝沈假球案,当年沈阳海狮奇迹般地保级成功,迄今还是个巨大谜团。事后主教练称球队有人赌球;还有1995赛季延边消极比赛,是中国足坛首次爆出消极比赛情况。赌球和为保级踢假球可能与竞争平衡水平的变化有关,当然这只是一种对动态竞争平衡可能的影响因素,造成动态竞争平衡落差大的原因是多方面的。
4.2 中超动态竞争平衡存在两个明显的相对稳定期,但动态竞争平衡水平存在较大的差距
1996—1998与2002 —2005赛季在整个联赛相对较为平稳的时段,1996赛季的肯德尔相关系数是2005赛季的3.39倍,存在一定的差距。1996—1998赛季动态竞争平衡表现出较为平稳的态势,但动态竞争平衡水平较低,大连万达、上海申花和北京国安俱乐部基本就是前3名,其他球队没有进入前3名。而2002—2005赛季球队等级相关系数较小,连续几个赛季等级相关系数较低,这几个赛季是中超整个历史最为平稳的几年,动态竞争平衡水平较好。3个赛季3支不同的球队获得了冠军,所有球队的排名发生了较大的变化,动态竞争平衡水平较好,联赛球队竞争平衡水平都有所提高。2002—2004赛季联赛有15支球队,开放式联盟很少出现球队数是单数的情况。如果球队数是单数,赛季最后一场比赛结束时间不同,有的球队提前一轮结束赛季比赛,而没有结束赛季比赛的球队打假球的可能性增大;并且2002、2004和2005赛季没有降级制度,从相邻赛季等级相关系数来看,动态竞争平衡水平可能与联赛的球队数、升降级制度相关。联赛如果没有升降级制度,球队对取胜的欲望降低,这样可能制约动态竞争平衡水平的提高。
4.3 中超动态竞争平衡波动较大,但是动态竞争平衡水平有提高的趋势
中超过去的赛季中动态竞争平衡波动较大,肯德尔相关系数最小的是0.033,最大的是0.485,最大是最小的14.7倍,动态竞争平衡水平差距较大。大约8个赛季的动态竞争平衡水平在低位运行,动态竞争平衡水平较差。但还有7个赛季处于相对较高的动态竞争平衡水平,动态竞争平衡水平相对较好,弱队战胜强队的可能性相对较大。对τ值显著性差异进行检验,P>0.05的赛季有6个,P<0.05的赛季有9个,显著性水平大于0.05的赛季占到67%,说明赛季排名独立性较强的赛季占到多数。本研究还对中超15个赛季肯德尔相关系数进行回归分析,得到回归方程为:τ=-0.002t+0.338,斜率为负数,t代表赛季的时间,1995—2009赛季依次为1~15,从以上分析可以说中超动态竞争平衡水平有提高的趋势。
5 结论
1)从动态的角度对中超的竞争平衡情况进行分析是一种更为全面的分析。多数研究是从静态的视角分析,是一种相对孤立、静止的状态,只反映单赛季的竞争平衡情况,不能反映球队连续赛季的排名变化情况。而动态竞争平衡是一种更为全面的衡量视角,可以反映相邻赛季之间球队排名变化的情况,对相邻赛季所有球队的排名变化都可以关注,相对静态而言动态竞争平衡是一种较为全新的视角。
2)采用肯德尔等级相关系数法衡量中超动态竞争平衡是一种相对科学合理的方法。中超球队相邻赛季的排名是一组定序变量,采用肯德尔等级相关系数完全适合衡量相邻赛季之间排名变化的相关程度。
3)中超动态竞争平衡整体来看波动较大,最高与最低竞争平衡水平差距较大。尽管有两个明显的相对稳定期,一个处于高位,一个处于相对的低位,但维持时间较短。由于中超的历史并不长,竞争平衡水平波动太大,从一定程度上反映了联赛的不成熟,但是对赛季肯德尔相关系数进行回归分析发现中超动态竞争平衡水平有提高的趋势。
[1]Jonathan Michie,Christine Oughton.Competitive Balance in Football:Trends and Effects[Z].The SportsNexus,2006,1-38.
[2]Andrew Larsen,Aju J.Fenn.Erin Leanne Spenner.The Impact of Free Agency and the Salary Cap on Competitive Balance in the National FootballLeague[J].Journalof Sports Economics,2006(7):374.
[3]余建英,何旭宏.数据统计分析与SPSS应用[M].北京:人民邮电出版社,2003:191-204.
[4]劳伦斯·纽曼.社会学研究方法[M].北京:中国人民大学出版社,2007:442.
[5]Kendall,M.and J.D.Gibbons.Rank Correlation Methods[M].London:Edward Aronold,1990:5.
[6]中国足球协会官方网站[EB/OL].http://www.fa.org.cn/,2010-4-20.
[7]Utt J,R Fort.Pitfalls to Measuring Competitive Balance with Gini Coefficients[J].JournaL of Sports Economics,3(4):367-373.
[8]Quick J,C Oughton.Pay Dirt:The Business of Professional Team Sports[M].Princeton.NJ:Princeton University Press,1992.
[9]Fort R.Thinking(some more)About Competitive Balance[J].Journal of Sports Economics,2003(4):280-283.
[10]Mizak,Daniel,Anthony Stair,andArmond Rossi.Assessing alternative competitive balance measures for sports leagues:a theoretical examination of standard deviations,gini coefficients,the index of dissimilarity[J].EconomicsBulletin,2005(12):1-11.
[11]Rodney Fort and Joel Maxcy.Competitive Balance in Sports Leagues:An Introduction[J].Journal of Sports Economics,2003(4):154.
[12]JoelMaxcy,MichaelMondello.The Impactof FreeAgencyon Competitive Balancein North American Professional TeamSports Leagues[J].Journal of SportManagement,2006,20:345-365.
责任编辑:郭长寿
Dynam ic Competitive Balance of China Football Association Super League
ZHANG Baoyu,ZHANG L in,WANG Yan
(Institute of Sports Event Research,Shanghai Sport U niverisity,Shanghai200438,China)
By using the m ethods of literature and statistics and from a dynam ic perspective,the paper analyzes the competitive balance of China FootballA ssociation SuperLeague.It finds that its dynam ic competitive balance fluctuates great and has poor stability,but the level of dynam ic competitive balance presents the trend of increase.
Chinese Football Association Super League;dynam ic competitive balance;Kendall’s rank correlation coefficient tau
G843
A
1004-0560(2010)06-0121-04
2010-08-24;
2010-09-12
国家社会科学基金项目,编号:06XTY001。
张宝钰(1974-),男,讲师,博士研究生,主要研究方向为体育教育训练学。
