商品房销售面积回归模型新论
2010-09-29胡静波
胡静波
(浙江长征职业技术学院,浙江 杭州 310023)
商品房销售面积回归模型新论
胡静波
(浙江长征职业技术学院,浙江 杭州 310023)
采用6个变量,运用回归分析工具,建立杭州市商品房销售面积的多元线性回归模型。经过对其拟合效果和假设检验,证明该模型的合理性和经济意义,在此基础上对杭州市未来商品房销售面积进行预测,并实证分析经济发展与商品房销售面积的内在联系。
商品房;销售面积;回归模型
1.变量选取
回归方程的自变量采用该城市经济发展的六个相关指标,包括“零售物价指数”、“GDP指数”、“新增人口”、“居民储蓄余额”、“居民新增储蓄余额”、“城镇居民可支配性收入”; 回归方程的因变量采用“商品房销售面积”(表1)。

表1 杭州市商品房销售及相关数据
2.商品房销售面积的多元线性回归模型
首先,用Excel回归分析工具建立多元线性回归方程。其中:y:商品房销售面积(万平方米);x1:零售物价指数(无量纲);x2:GDP指数(无量纲);x3:新增人口(万人);x4:居民储蓄余额(亿元);x5:居民新增储蓄余额(亿元);x6:城镇居民可支配性收入(元)。
选取置信水平为95%,即α=1-0.95=0.05,α/2= 0.025。
回归分析工具的运行结果见表2。
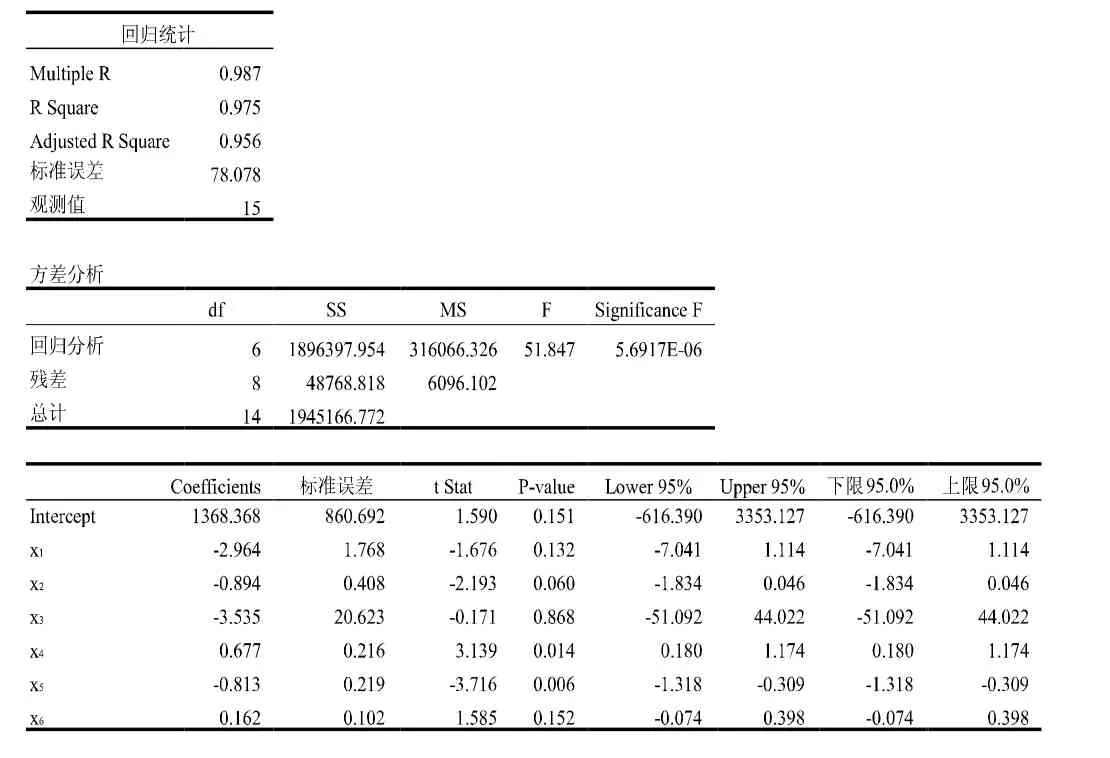
表2 杭州市商品房销售面积多元线性回归结果
回归方程的常数项以及六个自变量的回归系数从表2的Coefficients列得到,回归方程的表达式为:y=1368.368-
3.回归方程的拟合效果和假设检验
3.1 回归方程的拟合效果
从表2可知,(1)式的复相关系数为0.987,R2为0.975。这说明这个总平方和中,回归方程可以解释的比例占97.5%,误差平方和只占总平方和的2.5%。因此(1)式的拟合度是相当高的。
蓄电池综合运行状态主要由其寿命即充放电轮次反映,又主要与其放电电流密度、温度、放电深度、维护状况和贮存时间等有关,放电度越深,使用寿命越短。综合上述蓄电池物理属性,结合蓄电池自身内部电流、电压、内阻等属性,通过建立放电轮次—内部外部属性之间的关联模型,可实现蓄电池寿命的预测,提供蓄电池设备投运与报废指导。传输设备总体运行状态主要由其故障率反映,通过建立传输设备的历史故障情况与其运行环境、内部属性之间的关联模型,可实现运维人员对传输设备整体情况的把握;在此基础上,通过对设备趋势性劣化的监视,可实现故障预测,提升通信运维水平。
为了进一步说明(1)式的拟合效果,将表1中每年的五个自变量数据代入(1),计算样本量y的预测值(y),并计算预测值和实际值的误差,结果如下。

图1 (1)式计算的商品房销售量的预测值和实际值比较
由此可知,其中1996年、2000年、2003年和2006年四年预测值和实际值的误差较大,其余11年的预测误差都在10%以下。用(1)式计算的y对实际数据的拟合效果还是比较好的。特别是回归模型的预测值正确反映了商品房销售量2008年比2007年大幅下降。
3.2 回归方程总体显著性的F检验
表2中,回归方差MSR=316066.326,残差方差MSE=6096.102,F统计量=MSR/MSE=51.847,分子自由度df1=15-1=14,分母自由度df2=15-6-1=8,95%置信水平下,F检验的拒绝域右临界值为:FINV((1-0.95)/2,df1,df2)=FINV(0.025,13,8)=4.162。由于F=51.847> 4.162,(1)式的总体效果是显著的。
3.3 回归系数显著性的t检验
回归系数的自由度为n-k-1=15-6-1=8,95%置信水平的t临界值为TINV(0.05,8)=2.306。由表2可知,x4、x5的回归系数的t统计量的绝对值都大于2.306,因此这两个自变量的回归系数都是显著的。x1、x2、x3、x6的回归系数的t统计量的绝对值都小于2.306,可见这四个自变量的回归系数检验是不显著的。
4.“商品房销售面积”的逐步回归模型
(1)式中,x4、x5、x6的回归系数分别为0.677、-0.813和 0.162,这三个系数的实际意义是:居民储蓄余额每增加1亿元,商品房销售面积将会增加0.677万平方米,居民新增储蓄余额每增加1亿元,商品房销售面积将会减少0.813万平方米,城镇居民可支配性收入每增加1元,商品房销售面积将会增加0.162万平方米。
x1、x2、 x3、x5的回归系数都是负值,分别为-2.964、-0.894、-3.535和-0.813,这三个系数说明相应的自变量对“商品房销售面积”的边际贡献分别为:-2.964、-0.894、-3.535和-0.813。其中“GDP指数”和“新增人口”对“商品房销售面积”的边际贡献为负值,表面上看与实际情况不符。
产生以上情况的原因是由于自变量之间存在较强的相关性,称为变量的“多重共线性”。回归方程中自变量存在多重共线性,会引起变量的回归系数失真。
将表1的数据,选择“商品房销售面积”为因变量,其他五个变量为自变量,逐步回归准则选用“tvalues”,逐步回归选项选用普通逐步回归,进入的t值和排除的t值都选用1.0。逐步回归结果表明对于给定的t-Stat判据为1.0的前提下,没有其他的变量可以进入回归方程,回归方程中也没有需要排除的变量,PHStat逐步回归算法结束。
PHStat最终选择了自变量x2、x4、x5进入回归方程,得到回归方程:

(2)式的变量个数k=3,95%置信水平下t检验的临界值为:TINV(0.05,15-3-1)=TINV(0.05,11)=2.20,变量x4的回归系数为4.003,大于2.20,变量x5的回归系数为-3.972,绝对值大于2.20,变量x2的回归系数为-1.912,绝对值虽然没有超过2.20,但只相差0.288,因此可以认为三个变量的回归系数t检验都是显著的。
95%置信水平下,F检验的拒绝域右临界值为:FINV((1-0.95)/2,df1,df2)=FINV(0.025,13,15-3-1)=FINV(0.025,13,11)=3.391。因此(2)式的F检验也是显著的。
三个自变量“GDP指数”、“居民储蓄余额”和“居民新增储蓄余额”用(2)式计算“商品房销售面积”的预测值见表4。

表3 (2)式的预测值和实际值的比较
由此可见,(2)式对“商品房销售面积”的拟合效果虽然比(1)式稍差,但总体来说,也还是比较好的。1995-2009年间商品房销售面积预测值与实际值的偏差,除了1995、1997、2002、2003这4年偏差在20%以上外,其他年份的偏差都在20%以内,尤其是2007至2009年连续3年的偏差值都在10%以内。
房地产市场除了与一些经济变量密切相关外,还与政策相关。排除房地产业政策影响因素,总体而言,根据(2)式计算出的结果与实际值的拟合效果较好。而与(1)式相比,(2)式更加简洁。因此,用逐步回归得到的回归方程(2)可以作为“商品房销售面积”分析和预测模型。
5.用回归方程预测2010年商品房销售面积
根据(2)式,商品房销售面积=189.265-0.247GDP指数+0.760居民储蓄余额-0.857居民新增储蓄余额,用该回归方程可在预测三个自变量的基础上,预测2010年的商品房销售面积。

表42010 年杭州市若干指标预测
分别将x2、x4和x5的预测值代入(2)式,得到2010年商品房销售面积的预测值为:1440.27万平方米。
以上计算表明,在地区宏观经济指标的拉动下,2010年商品房销售面积,将与2009年的1441.18万平方米基本持平,说明杭州市商品房销售面积在2009年较大幅上升后,2010年将趋向稳定。
6.结 论
本文用回归分析方法对房地产业进行经济分析,建立了以“商品房销售面积”为因变量,以地区宏观经济变量“零售物价指数”、“GDP指数”、“新增人口”、“居民储蓄余额”、“居民新增储蓄余额”、以及“城镇居民可支配性收入”为自变量的多元线性回归模型。利用Excel回归分析工具,计算了相应的回归系数,得到了相应的多元线性回归方程。并进一步用逐步回归工具,对自变量进行了筛选,得到了以地区宏观经济变量“GDP指数”、“居民储蓄余额”和“居民新增储蓄余额”为自变量的线性回归方程,可以用这个回归方程对未来商品房销售面积进行预测。
对于其他城市或地区商品房销售面积的预测,也可以通过这样的方法进行研究。尽管建立选取的自变量可以不尽相同,得到的回归方程可能各异,但用回归分析和逐步回归分析的研究方法则应该是普遍适用的。
相关的经济决策部门可以运用回归分析的方法,在跟踪和预测GDP指数、居民储蓄余额、城镇居民可支配性收入等地区宏观经济变量的基础上,前瞻性地制定房地产业的调控政策,以更好地配置公共资源,促进房地产市场稳步健康的发展。
[1]刘纪辉.基于多元线性回归分析房地产价格的影响因素.湖北工业大学学报,2008,23(4):87-90.
[2]孙霄飞.回归分析在房地产销售中的应用.科技咨询导报,2007(26):168-169.
[3]Evans,JamesR.数据模型与决策.中国人民大学出版社,2006.
[4]刘畅,从静,李民.房地产需求的分析与预测.建筑管理现代化,2005(3):30-32.
[5]葛金辉,桑玉杰.回归模型在房地产市场方面的应用.沈阳航空工业学院学报,2003,20(4):69-70.
(责任编辑:张巧燕)
