一种网络编码构造算法研究

胡 平

(南京邮电大学 电子科学与工程学院，江苏 南京 210003)

在目前的通信网络中，不管是采用电路交换还是采用分组交换的方式传输信息，中间节点都仅仅转发或存储转发它所接收到的信息，除了数据复制以外，网络的中间节点并不需要做任何其他的数据处理。

2000年，Ahlswede等人发表了一篇题为“网络信息流”的文章，提出了“网络编码”这一概念，该理论通过允许中间节点在转发信息前对输入信息流进行编码，以实现网络组播容量的极限。但这只是给出了网络最大信息传送速率的存在性证明，并没有给出具体的网络编码实现方式。Li、Yeung和Cai[1]提出单一信源、多接收节点网络的最大传输速率可以通过线性网络编码实现；Koetter和Medard[2-3]为网络编码设计了一个数学框架。另外Sanders等人提出了一种实现网络编码的多项式时间算法[4-5]，这种方法将网络编码的构造进一步简化。

上述方法都是基于已知整个网络的拓扑信息。Chou等提出了不需网络拓扑信息的分布式网络编码[6]。另外，现在关于网络编码和其他方面结合的研究也很多，例如网络编码和纠错码的结合、网络编码和加密体制的结合等。

1 网络编码原理

在研究网络编码的过程中，通信网一般简化为相应的图来表示。假定有一个(如图1所示)的通信网络，这是一个拥有单个信源和2个接收节点的网络，假设每条链路都无时延和无差错。其中，s是信源节点，y和z是接收节点。图1(a)给出了每条边的信息速率均为1 bit/单位时间。由最大流最小割定理容易得出从信源s到接收节点y和z的最大流均为2。由此得到信源s可以同时发送2 bit信息给y和z。但是，如果按如图1(b)传统路由方式，在1个单位时间内将无法完成以上传输。图1(c)给出一种编码方案，从图中可以看出，为了从信源节点s同时传输2 bit信息b1，b2到接收节点，则在中间节点 w处，必须通过网络编码，使输出边(w，x)传输 2条输入边上所携带信息的线性组合 b1+b2(模 2加)，那么在接收节点 y和 z处，才可分别由 b1+b2和 b1、b1+b2和b2通过模2加恢复出所有的信息 b1、b2。因此，在这个简单的组播问题中，中间节点w不再只进行简单的存储转发，而是引入一定的操作，从而可以在1个单位时间内把 2 bit的信息传输给接收节点 y和z，这就是网络编码的思想。

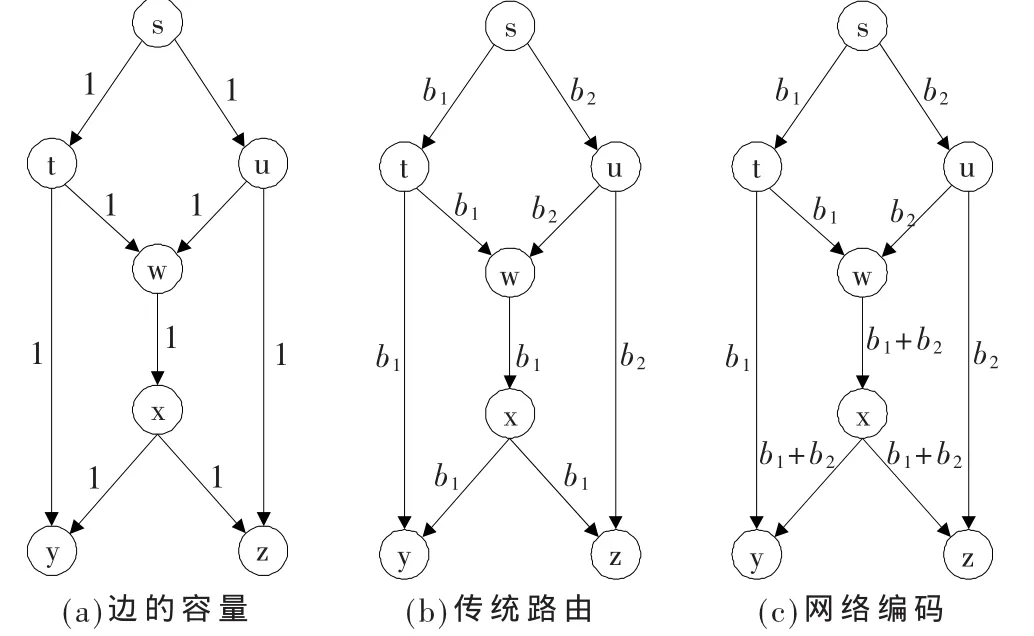
图1 经典网络编码原理图

网络编码的定义：网络中的节点对信息bit流进行一定的操作，如模 2“加”、“与”、“或”等，而不是仅仅对其进行复制转发。

2 线性网络编码

通信网络G=(V，E)上的线性码组播(LCM)是指给通信网络中的每个节点 v∈V分配向量空间Ω′(v)，同时给每条边e∈E分配全局编码向量Ve(e)。其中：

(1)Ω′(s)=Ω。

(2)Ve(e)∈Ω′(v)对每一个 e=(v，v′)。

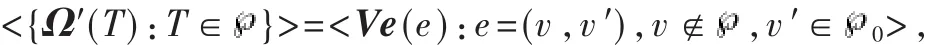
<·>代表其中的向量张成的空间。

(4)对节点T输出边分配的编码向量是其输入边所分配的编码向量的线性组合。

LCMV刻画了一种信息数据在网络中传播的结构。将信源节点s要传输的信息分成h维的向量组，称作信息向量。在传输过程中，一条边上承载的数据符号是信息向量和该边所分配的向量的向量积。

对于图中的通信网络，网络编码的基域为 F2，可以如下给各条边分配全局编码向量：

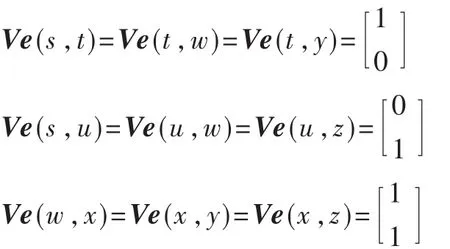
信源s的信息向量为(b1b2)，每条边上传输的信息符号为信息向量(b1b2)和该边的编码列向量的向量积。

3 有环网络的网络编码

上面考虑的网络编码都是基于无环无时延的，不具有一般性意义。

当信息流在有环网络传播的时候，时延成为构造网络编码必须要考虑的问题。为了数学上的方便，将环上节点处理的时延设为1个单位时延。这与卷积编码器有关，卷积编码器由一系列移位寄存器和加法器构成，即信息流通过有时延的节点相当于通过移位寄存器。

当网络图存在1个或多个环时，假设每个节点都有单位时延，把网络图看成是有限域网络卷积码的组合，则移位寄存器的个数等同于图中边的数量。

把有环网络分为两部分：(1)先将其看作是个无环无时延网络，分配其编码向量；(2)考虑每个节点的时延，设当前时刻为 t，k个单位时延的因子即为 σ(t+k)，则求出的编码向量即为Ve(e)·σ(t+k)。

4 基于有环网络的代数构造算法

基于有环网络如代数构造算法如下：

(1)引入系统转移矩阵来描述输入变量与输出变量之间的关系。设节点v是网络中的唯一信源，用x=(X(v，1)，X(v，2)，…，X(v，μ(v)))来表示信源 v 的输出，其中X(v，μ(v))是一个离散随机过程，μ(v)表示信源的出度。置用 z=(Z(v，1)，Z(v，2)，…，Z(v，η(v)))来表示信宿节点v 的输入。同理，Z(v，μ(v))是一个离散随机过程，η(v)表示信源v的出度。则输入变量和输出变量之间的关系可以表示为：z=xM，其中M称为系统转移矩阵。所以，要想在信宿节点由接收到的消息向量z得到信源输入x，则必须要求系统转移矩阵M的行列式不为0。

(2)已知通信网络的信源输出矩阵A，信宿节点输入矩阵 B，网络的邻接矩阵 F，则系统转移矩阵M=A(IF)-1BT，其中 I 是一个|E|×|E|的单位阵。

(3)可以将系统转移矩阵M的每一个列向量作为每条边分配的编码向量。

(4)以及将网络图简化，可以把网络图可以分成几个子集合，使它们具有相同的特性：①每1个子集合只含有1个信源节点或1个编码节点；②1个既不是信源节点也不是编码节点的节点属于1个子集合，这个子集合包含它最近的祖先编码节点或信源节点。“子树分解”把1个网络划分为不同的子图，而属于同1个子图的所有节点流过的信息流都是相同的。对1个编码设计问题来说，只需要知道怎样相连，而1个子树里面的网络结构是什么样的却并不起什么作用。因此，可以把每1个子图看成1个节点，并保留连接子图的边。

(5)通过一个环记为1个时延，即信息流通过有时延的节点相当于通过移位寄存器。用一系列移位寄存器和加法器构成网络图，并求出时延因子σ，每条分配的编码向量为 Ve(e)·σ。

本文简要介绍了网络编码以及线性网络编码的基本原理，提出了一种基于有环网络的改进代数构造算法，有效地解决了网络中存在环路时的编码问题。网络编码技术方兴未艾，研究前景十分广阔。

[1]LI S R，YEUNG R W.Linear network coding[J].IEEE Transaction on Information Theory， 2003，49(2)：371-381.

[2]KOETTER R， MEDARD M.Beyond routing：an algebraic approach to network coding[J].IEEE Computer and Communications Societies， 2002，1(1)：122-130.

[3]KOETTER R，MEDARD M.An algebraic approach to net-work coding[J].IEEE Transactions on Networking， 2003，1(11)：782-795.

[4]SANDERS P，EGNER S.Polynomial time algorithms for network information flow[M].New York， USA：ACM， 2003.

[5]JAGGI S， SANDERS P， CHOU P A， et al.Polynomial time algorithms for network code construction [J].IEEE Transaction on Information Theory， 2005，51(6)：831-836.

[6]CHOU P A，WU Y，JAIN K.Practical network coding[C].In 41stAnnualAllerton Conference on Communication Control and Computing，2003.