MPI下单源点最短路径的并行算法设计与分析

黎 源，王会进

(暨南大学 信息科学技术学院，广东 广州510632)

随着高性能技术的发展，并行处理在解决人类重大挑战问题方面发挥着越来越重要的作用。并行计算从传统的超级计算机平台，转移到一组高性能节点或工作站/PC机构成的称之为集群的计算平台上，机群成为并行计算平台的一个趋势。并行程序设计是并行处理的核心技术。MPI(Message Passing Interface)即消息传递接口，是一个由众多并行计算机厂商、软件开发单位/组织、并行应用单位等共同维护的标准，是目前最流行的分布存储并行编程环境。本文基于MPI进行并行程序设计的研究工作。

1 研究背景

平面中带权图中的最短路径问题是计算机科学中一个被广泛研究的对象，目前出现了大量并行求解最短路径问题的算法。Chandy和Misra提出了一种计算k个最短路径问题的并行算法，该计算将所有顶点到给定顶点的k个最短路径之间的复杂度表示为O(m+nlog2n+nk)[1]。已知的最好的算法是Cohen[2]提出的运行在EREW PRAM上的算法，该算法在空间复杂度为O(n3/2)时的时间复杂度为O((log2n)4)。Traff[3]等人基于前缀计算、列表分级、排序等方法实现了Dijkstra串行算法的并行版本。Adamson、Tick[4]和 Traff[5]使用一个分布的共享存储器使标签设定算法并行化。由于同一时刻只是具有最短距离标签的节点才能从队列中取出，因此实验中观察到标签设定算法具有弱并行性。Traff通过允许处理器取出多于一个的节点来改善性能。Romeijn和Smith[6]通过在分布式网络中求解近似最短路径树来尝试减少标签设定算法的通信要求。Bertsekas等人[7]对几个并行标签算法在有8个处理器的共享存储机器上作了实验比较，结果发现有一些算法有超线性加速比，一些则没有。Papaefthymiou和Rodrigue在CM-5上实现了Bellman-Ford-Moore算法，并比较了粗粒度划分和细粒度划分之间的差异。此外，其他衍生出来的算法，还有平衡二叉树的标签设定算法、单队列的标签修正算法、双队列的标签修正算法等。本文基于多进程环境把Dijkstra串行算法转化为并行算法，该算法采用按列分块，适合于无向图或有向图的求解。

2 Dijkstra并行算法的设计

设图G(V，E)是一个有向加权网络，其中V是顶点的集合，E是边集合。使用连接矩阵W来表示图，边上权 值 w[i][j]>0,i,j∈V，V={0，1，…，n-1}，dist(i)表 示 为最短路径长度。

2.1 数据划分

为了使程序由各个处理器独立地执行，必须要找到可以并行性的操作。

常用的数据划分方法有行划分、列划分和分块划分等。由于每次内循环都要使用到某一定点到其他顶点的权值，而且当图G(V，E)是有向图的时候，权值矩阵非对称，因此此算法不适宜使用行划分。在此使用按列分解的方法。

分别为每个处理器分配若干的节点求得局部最小值，然后再将各个处理器求得的最小值进行归约，将归约得出的最小值广播到每个处理器中。

为了得到一种能够负载平衡的数据分解方法，可以对每个进程分配⎿n/p」或「n/p⏋个元素。这里使用的是按列分解方法，假设有节点数目是n，进程数是p，进程 i控制的第一列是⎿in/p」，进程 i控制的最后一列是⎿(i+1)n/p」-1，对于特定的列 j，控制它的进程是⎿(p(j+1)-1)/n」，任意两个进程控制的列数相差不会超过1。数据分割的结果如图1所示。

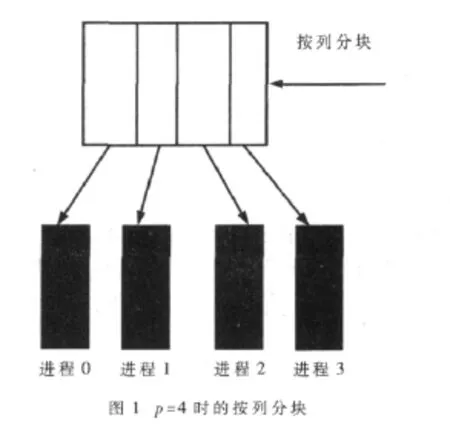
按图1所示的数据划分，则分布在不同进程i上的数据分别是 w(n，i×n/p：(i+1)×n/p-1)，其中 i×n/p：(i+1)×n/p-1代表取第 i×n/p列到第(i+1)×n/p-1列的数据。

2.2 Dijkstra并行算法实现

Dijkstra并行算法伪代码可表示为：

(1)MPI_Init(&argc，&argv)；

(2)MPI_Comm_size(MPI_COMM_WORLD，&p)；

MPI_Comm_rank(MPI_COMM_WORLD，&my_rank)；

(3)0处理器读入邻接矩阵和起始点s，分发邻接矩阵到各个处理器，广播s。

(4)//初始化各个处理器的数据

(5)//每次循环分别求出到达一个结点的最小值

③/*通信域中的每一个进程通过local结构把它的（数值、下标）对传递给MPI_Allreduce。当函数返回时，最小值和相关的下标存放在global结构中。

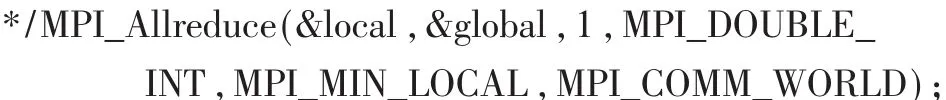
④//更新源点s到每个顶点的距离

⑤//把顶点 global.index对应处理器的//bdist[i]值改为true

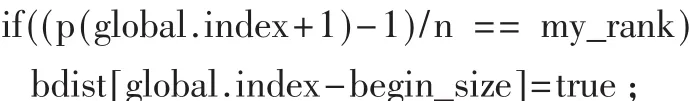
⑥MPI_Barrier(MPI_COMM_WORLD)；

(6)输出各个处理器求出的dist[i]值。

(7)MPI_Finalize()；

3 算法分析

3.1 算法复杂度

串行版本的Dijkstra算法的时间复杂度为O(n2)。

初始化各个处理器数据的时间复杂度为 O(n/p)，在算法的内循环①部分求出局部最小值以及相应的索引，最多执行「n/p⏋次，因此时间复杂度为 O(n/p)；③部分对一个长度为1的数据进行全归约。由于归约p个处理器需要「log2p⏋个消息传递步骤，总的时间复杂度为O(「log2p⏋)；④更新源点到其他顶点距离的时间复杂度为O(n/p)；⑤更新最小值对应的bdist[i]需常数时间。

最外层执行n-1次。

因此，并行算法的总的时间复杂度为：

即O(n2/p+nlog2p)

3.2 加速比和效率

设Ψ(n，p)表示为p个处理器上解决问题规模为 n的问题的加速比，ε(n，p)表示为在 p个处理器上解决规模为n的并行计算效率。作以下定义：

定义1：加速比=串行执行时间/并行执行时间。

定义2：效率=加速比/使用处理器数。根据定义得到：

随着数据规模的增大，计算量增加速度比通信量开销增加更快，因此该系统随着数据规模的增大可以取得更好的加速比和效率值。

3.3 等效指标

在研究中发现并行算法可以分为以下3类：

(1)必须串行执行的计算，用 σ(n)表示；

(2)可以并行执行的部分，用 φ(n)表示；

(3)并 行 开 销(通 信 操 作 和 冗 余 计 算)， 用 κ(n，p)表示。则得出一个加速比的完整的表达式为：

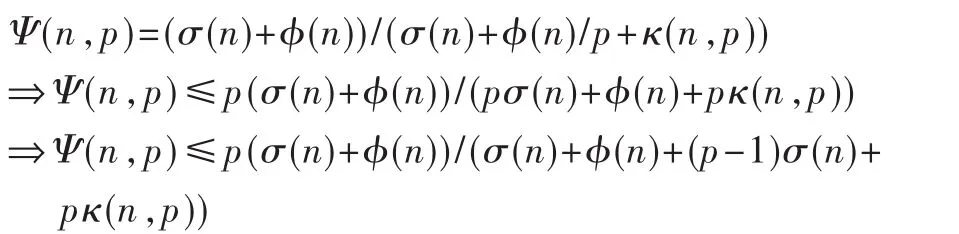
定义T0(n，p)代表所有进程花费在原有串行算法以外操作的全部时间。其组成是(p-1)个进程花在进程的内在串行部分的时间，以及p个进程花费在处理器通信和冗余计算上的时间。 所以将 T0(n，p)=(p-1)σ(n)+pκ(n，p)代入上式，得到：

T(n，1)代表串行执行时间，即：

如果效率不变，那么 ε(n，p)/(1-ε(n，p))是一个常数，上面公式可以化为：

由于在处理器个数增加时并行开销会增大，因此要保持效率就要增加问题的规模。假定一个并行系统具有等加速比关系：n≥f(p)。如果M(n)表示规模为n的问题所需的内存大小，M-1(n)≥f(p)则表示为了保持效率不变所需的内存与处理器个数p的函数关系。M(f(p))/p称为可扩展函数，其复杂度确定了可保持常数效率的处理器个数范围。

Dijkstra串行算法的时间复杂度是O(n2)。并行算法中全归约的复杂度是O(nlog2p)，每个处理器都参与了此步骤，因此

T0(n，p)=O(nplog2p)，因此并行算法的等效关系为：

串行算法中问题规模n所需的内存容量为n2，即M(n)=n2，此系统的可扩展性函数为：

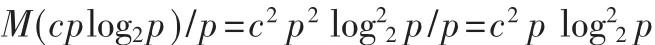
即每个处理器的容量随p增加。由于内存容量的限制,处理器的个数不能一直增加，因此此系统处理器的个数应在内存允许的范围之内才能取得最好的效果。

本文在mpi环境下设计了求单源点最短路径的Dijkstra并行算法，分析了该算法的时间复杂度、加速比、效率以及等效指标。理论证明了利用多处理器共同计算的优点，使若干台计算机就能完成大型计算机所完成的计算功能，解决了单计算机内存不足的问题，降低了计算成本，提高了程序的效率。在实际应用中，还要考虑到计算机之间的通信速度，这对计算性能的提高与否有重大影响。并行计算在未来的大规模计算中也会日益发挥重要的作用，如何提高并行性和进一步减少通信开销是将来要改进的工作。

[1]袁贞明，张量.GIS的前k个最短路径分布式多线程实现[J].计算机工程，2005，31(9)：37-38，162.

[2]COHEN E.Efficient parallel shortest-paths in digraphs with a separator decomposition[J].Algorithms，1996(21)：331-357.

[3]TRAFF J L，ZAROLIAGIS C D.A simple parallel algorithm for the single2source shortest path problem on planar digraphs[J].Journal of Parallel and Distributed Computing，2000，60(9)：1103.

[4]ADAMSON P，TICK E.Greedy partitionecd algorithms for the shortest path problem[J].International Journal of Parallel Programming，1991，20：271-298.

[5]TRAFF J L.An experimental comparison of two distributed single-source shortest path algorithmns[J].Parallel Computing，1995，21：1505-1532.

[6]ROMEIJN H E，SMITH R L.Parallel algorithms for solving aggregated shortest path problems[D].The University of Michigan，September 1993.

[7]BERTSEKAS D，GUERRIERO F，MUSMANNO R.Parallel asynchronous label-correcting methods for shortest paths[J].Journal of Optimization Theory and Applications，1996，88：297-320.