变阻力切削过程伺服系统的模糊控制*

张晓东

(广东白云学院机电工程系，广东广州 510450)

目前，数控伺服系统的驱动电动机的伺服控制一般只考虑到速度、位置和电流三个参数的控制，即所谓的三环控制［1］。实际上，在数控加工过程中，由于材料物理性能的不均匀(如铸件的疏松、夹杂和成分偏析，热扎钢的不均匀冷却导致的组织偏析等)，其切削阻力在随时改变。由于切削阻力的改变，必然导致伺服系统的不稳定，或者说，单方面的依靠增大伺服控制的增益不可能进一步提高加工精度，因为伺服系统的调节能力都是有限的。

切削阻力的改变必然导致伺服电动机电流的改变，如果仅仅依靠电流环的自身调节，达到的效果和所希望的结果往往是相反的［2］。在这种情况下，不是要稳定电流，而是要改变速度。所以，一切仅仅以追求“稳定”为目标的三环控制不可能达到这个目标。

对于电流环，快速性其是主要的性能指标，因为在受到扰动时，必须能够迅速调节，才能保证力矩最小。电流调节器不要求做到无静差调节［3］，因此电流调节器采用比例调节。

位置调节中采用对位置智能PID算法进行修正，一是采用积分分离的PID算法;二是采用神经网络模糊PID智能算法。系统进入积分环节后，会产生大的超调量，引入积分分离算法，以既保持积分作用，又减小了超调量，使控制性能有较大改善。智能PID算法则可在调节器进入期望位置点附近时实现零调节。

当位置误差|eθ(n)|≤E时，采用智能PID控制，可以保证系统的控制精度。

当|eθ|>E时，采用P控制，可以使超调量大幅度减小。

对于速度环和电流环的参数调整，主要是大量的离线测试，位置环的智能PID算法则是在线整定［4］。

1 神经网络模糊PID控制器的组成与设计

1.1 神经网络模糊PID控制器的结构

为了实现变阻力切削过程伺服系统的模糊控制，首先要构建神经网络模糊PID控制器，基于神经网络的模糊PID控制器系统结构如图1所示。控制器由三部分组成:

①传统PID控制器。直接对被控对象过程进行闭环控制，并且三个参数Kp，Ki，Kd为在线整定式。

②模糊化模块。对系统的状态变量进行模糊量化和归一化处理。这样做的优点是利用模糊控制的鲁棒性和非线性控制作用，对作为实现模糊规则神经网络NN的输入进行预处理，避免了NN的活化函数采用Sigmoid函数时，直接输入量过大而导致输出饱和，使得对输入不再敏感的缺点。

③神经网络NN。用于表示模糊规则，经过神经网络的学习，以加权系数的形式表现出来，规则的生成就转化为加权系数初值的确定和修改。根据系统的运行状态，调节PID控制器的参数，以期达到某种性能指标的最优化。即使输出层神经元的输出状态对应于PID控制器的三个可调参数Kp，Ki，Kd，通过神经网络的自学习，加权系数的调整，从而使其稳定状态对应于某种最优控制规律下的PID控制器参数。

1.2 神经网络模糊PID控制器的设计

1.2.1 PID控制的实现

数字PID控制器是将模拟PID控制算法离散化［5］，通过程序实现，因此使系统设计更灵活，方便。其离散PID控制规律为

式中:u(n)，e(n)分别为第n个采样时刻控制器输出量(PWM信号)和输入量(位置偏差信号);Kp为比例系数，Ki为积分系数，Kd为微分系数。

由式(1)可得到第n个采样时刻的控制量u(n)和第n－1个采样时刻的控制量u(n－1)之间的增量为

式中，Δe(n)=e(n)－e(n－1)。这样一旦确定了Kp，Ki，Kd，只要前后三次速度测量值的偏差，就可以求出控制增量。

1.2.2 系统状态变量的模糊化处理

在位置闭环系统中，角度指令是由上位机给定的，机床伺服系统的反馈信息由安装在电动机轴上的磁性编码器获得。这里定义角度设定值为rθ，系统反馈得到的位置信息是yθ(n)，位置误差为eθ(n)，则有

将eθ(n)作归一化处理，有

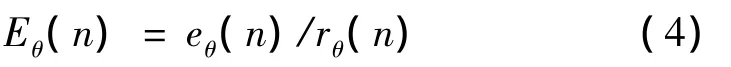
上式中Eθ(n)为eθ(n)归一化后的位置误差输入量，将其在闭区间［－1，1］内分成11个等级，完成“归档”模糊量化，如下式所示

Eθ为位置误差的模糊论域。为了将伺服电动机的位置误差信息传送给神经网络(NN)，对Eθ再进行“概念化”处理，如下:

式中:Eθ，n为 NN的一个输入变量;γ为缩减系数，取0.2。

1.2.3 BP 神经网络学习

BP神经网络是一种三层的神经网络。设定输入节点M=3，对应经过模糊量化处理后的系统状态变量。根据Hecht－Nielsen的理论和实际实验［6］，隐含层的节点数可取Q=2×3+2=8。输出节点数也为3，分别对应 PID控制器的三个可调参数Kp，Ki，Kd。由于Kp，Ki，Kd不能为负值，所以输出层神经元的活化函数取非负的Sigmoid函数，而隐含层神经元的活化函数可取正负对称的Sigmoid函数。

设定输入层中:

也就是说，输入层中三个输入量为n时刻以前三次采样获得的驱动电动机位置误差经过归档模糊化处理后的值。进而可求得网络隐含层的输入输出为

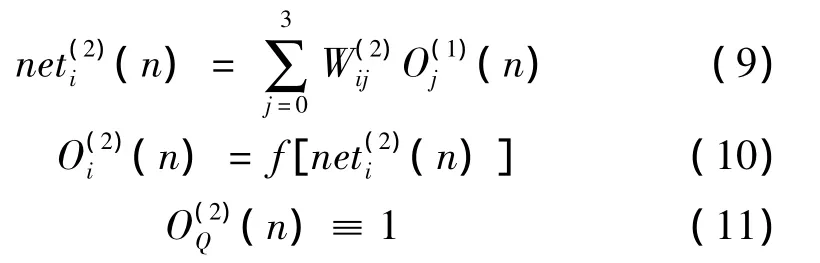
式中:为隐含层权系数;为阈值f［·］为活化函数;上角标(1)、(2)、(3)为输入层、隐含层、输出层。

最后，网络的输出层的输入输出为

式中:为输出层加权系数;为阈值g［·］为活化函数，g［·］=(1/2)

取性能指标函数

依据最速下降法修正网络的加权系数，即按J对加权系数的负梯度方向搜索调整，并附加一个使搜索快速收敛全局极小的惯性项，有

式中:η为学习速率;α为惯性系数。

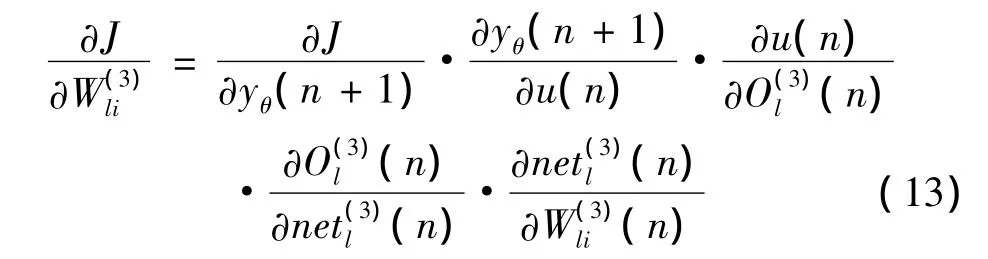
由于∂yθ(n+1)/∂u(n)未知，这里近似用符号函数 sgn(∂yθ(n+1)/∂u(n))取代，由此带来的计算不精确的影响可以通过调节学习速率η来补偿。

因此，可得BP神经网络NN输出层的加权系数计算公式

依据上述推算办法，可得隐含层加权系数的计算公式为

2 状态仿真实验

在实际调试过程中，根据RLS算法［7］估计模型参数，选取Np=Nc=4，λ=1，零均值单位方差的白噪声加在系统上;模型的非线性和耦合部分N(t)采用BP算法和由三层BP网络进行辨识;网络的输入元为12个，网络的隐元为9个。首先进行离线预训练［8］，使得

在式(16)中:N(t)代表系统参考输入，^N(t)代表系统输出。神经网络离线训练之后作为切削系统闭环自适应控制的初始网络，各层加权系数初始值取区间［－1，1］上的随机数。在给定一定的角速度指令后，由PWM电压信号经过功率转换后，驱动内有光电速度反馈部件，调速比为1:10 000的交流伺服电动机，其单位阶跃响应曲线如图3所示。

由图3可以看出，在一定的指令时间内，神经网络模糊控制器能够很好地完成角度指令的零误差调节。与常规PID控制器相比较，神经网络模糊控制器综合了三种控制的长处，既有模糊控制简单有效的非线性作用，又有神经网络的自学习和适应能力，同时具有PID调节的简单适应性，且很好地抑制了由于切削阻力变化导致的噪声信号及其干扰。

3 结语

(1)在一定的指令时间内，神经网络模糊控制器能够很好地完成角度指令的零误差调节。与常规PID控制器比较，神经网络模糊控制的超调量很小，而且不需要人工调整PID参数值。模糊PID控制系统将模糊神经网络与PID控制器结合起来，使PID控制器智能化，既可以加快控制的响应速度，又能够实时调整控制参数，提高控制精度。

(2)模糊PID控制比普通PID控制更有鲁棒性，模糊控制的知识表达能力和神经网络的在线学习能力，构成了性能更好的智能PID控制器。输出层神经元输出状态对应于PID控制器的三个可调参数Kp、Ki、Kd，通过神经网络自学习，加权系数调整，使其稳定状态对应于某种最优控制规律下的PID控制器参数。

(3)神经网络模糊控制器能够很好的完成角度指令的零误差调节，其综合了三环控制的长处，既有模糊控制简单有效的非线性作用，又有神经网络的自学习和适应能力，同时具有PID调节的简单适应性，对阻力干扰有较强的抑制能力。

1 Mamdani E.H.Develpoment in Fuzzy Logic Control［C］.Proc.of 23rdConference on Decision and Control，1984.

2 Man Z H，Yu X H and Ha Q P.Adaptive control using fuzzy basis function expansion for SISOlinearizable nonlinear systems.Proc［C］.of the 2ndAsia Contr.Conf.Soul.Korea，1997:695 －698

3 Slotine J J E and Coetsse J A.Asaptive sliding controller synthesis for nonlinear systems［J］.Int.J.Control，1998，43(6):1631 －1651

4 陈增强，袁著祉.PI型广义预测平均控制器及仿真［J］.控制与决策，1996(6):703～706

5 白连平，陈秀真.提高BP网络学习速度的自适应算法［J］.系统仿真学报，2001(8):97～98

6 Tan Y and De Keyser R.Neural network based adaptive predictive control［C］.Clarke D ed.Advances in model－ based Predictive Control.Lodon:Oxford University Press，1994，358 －369

7 李世勇.模糊控制·神经控制和智能控制理论［M］.哈尔滨:哈尔滨工业大学出版社，1998.