基于灰度数学形态学的遥感影像薄云处理方法

2010-09-28岳建平

测绘通报 2010年12期

关键词：形态学灰度运算

曹爽,岳建平,马文

(1.河海大学地球科学与工程学院测绘科学与工程系,江苏南京 210098;2.南京信息工程大学遥感学院测绘工程系,江苏南京 210044)

基于灰度数学形态学的遥感影像薄云处理方法

曹爽1,2,岳建平1,马文1,2

(1.河海大学地球科学与工程学院测绘科学与工程系,江苏南京 210098;2.南京信息工程大学遥感学院测绘工程系,江苏南京 210044)

遥感成像过程中薄云是最常见的一种噪声。在利用数学形态学进行薄云处理的基础上,探讨利用广义多结构元素的数学形态学进行薄云处理的方法,并对 SPOT图像进行试验。结果表明,该方法对薄云去除的处理效果有一定的改善和提高。

数学形态学;广义多结构元素;遥感影像;薄云去除

一、引言

从遥感影像中获取信息是学术界一直关注的课题之一。遥感成像过程中,云雾 (主要是薄云、薄雾)是最常见的一种噪声,它使获得的遥感图像模糊,分辨率下降,有用遥感信息相对贫乏[1]。去云处理不仅是对遥感图像进行准确解译的基础,也是增强遥感数据有效性、可用性的重要途径。它是遥感图像预处理中的一个重要环节,也是图像处理、图像分析的一大难点。目前,除合成孔径雷达传感器能穿透云层获取地表信息外,其他传感器均未能彻底解决影像数据的云覆盖问题。从 20世纪 90年代开始,遥感影像的云去除就成为一个活跃的研究领域。因此,运用图像处理技术,研究如何有效去除云雾的影响、提高遥感数据利用率具有重要意义。本文在研究数学形态学进行薄云处理的基础上,引入广义结构元素,旨在讨论一种新的薄云处理方法,更有效地去除薄云。

二、现有薄云处理方法

云覆盖类型不同,消除云的方法也不同。薄云雾覆盖区域,地面景物的光谱特征仍在一定程度上得以保留,对此可以通过大气纠正或数字图像处理的相关技术有效去除云雾影响,恢复地面景物信息。国内外对遥感图像云层干扰的去除作了大量的研究,提出了多种算法。薄云雾覆盖区信息恢复的方法与途径主要有以下几种：

1)基于光谱信息的薄云处理方法。这种方法对研究条件要求比较高,如果利用多光谱影像中某些波段对薄云的较强敏感性来提取薄云信息,有时会使遥感影像的某些波段缺失,且处理后的波段与原波段对应关系不明确,如缨帽变换法[2]。

2)基于影像融合的薄云处理方法。该方法操作简便,但是去薄云效果不是很理想,局限性很大[3]。

3)基于同态滤波的薄云处理方法。该方法利用同态滤波以及改进的同态滤波方法[4],根据薄云雾覆盖信息在频率域上通常占据低频信息的特点,将图像通过傅里叶变换转换到频率域,然后使用高通滤波器对影像进行空间滤波,除去云雾等低频信息。该方法忽略了影像的低频成分除薄云雾以外,还包含大量的其他背景信息的事实,因此,在去除低频云雾成分的同时,该方法也会削弱影像的其他背景信息,从而改变了一些区域的影像特性。

4)基于混合像元分解的薄云处理方法[5]。该方法充分考虑水汽环境的特点,把水体像元光谱看作水、污染物和气溶胶(薄云)等光谱的混合。混合像元模型能有效地消除薄云和气溶胶的影响,可实现更精确的水质信息提取。不过此方法主要针对水域影像薄云去除,应用受到获取数据等的限制。

5)基于直方图匹配的薄云处理方法[6]。该方法首先假设薄云覆盖区去除云影响后的图像特征与无云覆盖区图像特征相同,因此可以利用同一幅图像中非云覆盖区的图像特征作为参照,使云覆盖区的图像直方图与之匹配,达到消除云影响的目的。该方法不足之处在于假设条件有时并不满足,精确的云覆盖区范围的确定也有一定困难。

6)基于数学形态学的薄云处理方法。该方法利用数学形态学中的开、闭运算相结合可以分离高低频的特点,构造结构元素,进行薄云处理[7]。

三、基于灰度数学形态学的薄云处理

1.灰度数学形态学薄云处理的基本方法

数学形态学 (mathematical morphology)诞生于1964年,它应用最广泛的一个方向就是滤波作用,如将开、闭运算结合起来构成形态学噪声滤波器,而且数学形态学的并行运算对处理数字图像有很重要的意义,可以大大提高处理的速度。数学形态学中的基本运算是基于二值图像进行定义的,但实际遥感图像处理是针对灰度图像 (多值图像)进行的,因此,处理灰度图像时采用灰度数学形态学。利用灰度数学形态学的滤波算法来处理遥感影像中处于低频的薄云的基本步骤如下：

1)利用结构元素对含有薄云影像进行先闭后开运算,分离影像的高低频成分,即

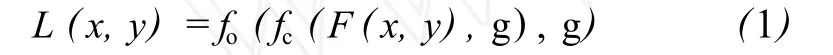
式中,x、y为影像坐标;F(x,y)为薄云影像的灰度函数;L(x,y)为影像的低频部分;fc为闭运算;fo为开运算;g为结构元素,一般取 3×3或 5×5的矩阵。

2)L(x,y)处理后获得的是薄云影像的低频部分。其中不但有云信息也有地物信息,只要选取系数 K将L(x,y)中的云分量求出,再由原影像将这部分减去,就可以得到去薄云后的影像。即

式中,F′(x,y)为去薄云后的影像;K为云所占低频的百分数,根据影像的薄云情况经验选取。

根据试验比较可知,灰度数学形态学中的先闭后开运算应用到遥感影像的去薄云处理中,可以达到去云的目的,云覆盖区域下的地物纹理更清楚,影像细节保持更好,目视效果与传统去云效果相比较也很理想。

2.数学形态学中的广义多结构元素

在数学形态学中,结构元素是最重要、最基本的概念,结构元素在形态变换中的作用相当于信号处理中的“滤波窗口”,就如卷积运算中的模板。不同的场合结构元素的选择及其相应的处理算法是不一样的,对不同的目标图像须设计不同的结构元素和不同的处理算法。结构元素的大小、形态选择合适与否,直接影响去云的效果。

开运算可以滤除图像中的峰值(正脉冲)噪声,闭运算可以滤除图像中的低谷 (负脉冲)噪声。传统的开运算和闭运算只采用了一种结构元素,因此滤波输出的图像中只保留了与这一结构元素相匹配的几何信息,而其他的几何信息与噪声一起被滤掉,所以不利于图像几何特征的保持。为了提高数学形态学滤波的有效性,采用多个结构元素并行处理的数学形态学滤波在图像滤波和特征提取方面获得应用。赵春晖[8]采用了多结构元素,构造了一类多结构元素并行复合形态滤波器。这类滤波器不仅可以有效地抑制图像中的噪声,而且较好地保持了图像的几何结构特征。

在多结构元素形态学的基础上,还可以采用多结构元素构造一类适于图像平滑并行复合形态的滤波器,分别称为广义形态开-闭最大滤波器和闭-开最小滤波器：

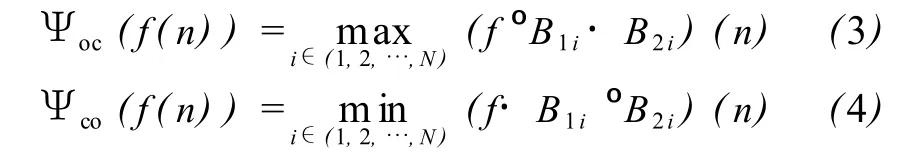
通过研究证明,传统的闭-开滤波模糊了图像的细节特征,滤波效果不好;普通的多结构元素虽然保持了细节,但不能完全达到滤波效果;而这种广义的形态闭-开最小滤波器不仅可以有效地抑制图像中的噪声,而且较好地保持了图像的几何结构特征[8]。

3.广义多结构元素在薄云处理中的应用

多结构元素的数学形态学应用到薄云处理中的基本公式为

式中,F(x,y)、L(x,y)、fc、fo含义同式 (1);g、b为不同形态的结构元素,且相对来说 g的尺寸比 b的尺寸小。

按多结构元素数学形态学薄云处理的基本公式,将广义形态闭-开最小滤波器应用于去除薄云中,相当于用两组结构元素组做不同结构元素不同尺寸的多结构元素薄云处理,之后再将两组薄云处理后的图在每一像元点进行比较,取最小值,得到的就是按广义形态闭-开最小滤波器薄云处理后的图像。例如:选用两组结构元素集,每个结构元素集中有两个结构元素,其中, B11为尺寸是 9像素的菱形结构元素,B12为尺寸是 9像素的方形结构元素,第二组元素组中的结构元素是比第一组结构元素尺寸大 5像素的一组结构元素,B21是方形结构元素,B22为菱形结构元素。分别用 B11与 B21、B12与 B22按式 (5)做闭-开运算,求出两组薄云处理后的图像,再对两组图像求最小值。

四、试验结果与分析

试验采用如图 1所示的 SPOT影像,接收时间为 10月份,该影像受到薄云以及厚云遮挡的影响,薄云最大的遮挡区域达到 166像素 ×200像素。选取薄云区域,利用Matlab编程,为了对比分析,对薄云区域分别用同态滤波(截止频率为 0.3),多结构元素(先尺寸为 5的菱形后尺寸为 9的方形结构元素)及广义结构元素(按第三章第 3节中尺寸)的数学形态学方法进行处理,处理结果如图2～图 4所示。

图1 原始图

图2 同态滤波去薄云

图3 多结构元素去薄云

图4 广义结构元素去薄云

从目视角度可以看出：①同态滤波方法使得薄云区域边缘锐化;灰度数学形态学中的先闭后开运算应用到遥感影像的薄云处理中,可以达到去云作用,云覆盖区域下的地物纹理清楚,影像细节保持更好,目视效果与传统去云效果相比较也很理想。②广义形态闭-开最小滤波器去薄云后的效果优于不同形态不同尺寸的多结构元素薄云处理的效果,在细节保持上更好,图4整体清晰度要比图3好,薄云处理后图4受结构元素形状的影响比图 3要小。通过比较可知,采用广义结构元素去云效果是最好的。

在遥感影像的空间域中,含薄云区域具有局部能量大、区域灰度平均值高、标准差小的特点,因此,本文对处理后的云影像进行统计分析,主要采用的评价指标是影像的均值、标准差和熵[13-14]。设影像为 f(x, y),大小为M×N,则各指标可如下定义

云影像均值要大于薄云处理后影像的均值,因此可用平均灰度评价去除薄云是否有效。标准差反映影像的信息含量,在遥感影像薄云处理中可以反映图像的细节信息变化情况。熵反映图像的信息含量,一般认为图像的熵越高越好。理想的薄云处理结果是,去薄云后的影像平均灰度降低,标准差和熵的增大表明所含信息量丰富。处理后的薄云影像数据分别按均值、标准差、熵进行统计,如表1所示。

表 1 薄云处理前后影像统计指标对比

从表 1可以看出各种薄云处理方法都使去除薄云后的影像的平均灰度值下降,说明各方法都达到了薄云去除的目的,本文所提出的数学形态学各种薄云去除方法也可以进行薄云处理。为达到理想的目视效果,各方法在处理时都选择无云参考区域进行直方图规定化,因此各方法处理后影像的平均灰度值比较接近。各种方法处理后影像的标准差都变大,说明处理后影像都变清晰。从表 1中的薄云影像及几种薄云处理后影像的熵统计值对比可以看出,几种方法处理后的图像的熵值与原影像的熵值相比较都变小,说明各种方法处理后影像的标准差都变大,熵值与原影像的熵值相比较都变小,说明各种方法在一定程度上都会去掉影像的细节信息。其中,数字形态学去薄云后的影像的熵值比同态滤波去薄云后影像的熵值大,说明数学形态学去薄云方法比同态滤波方法更好地保持了影像的细节信息,而且广义结构元素的数学形态学的熵值最大,说明这种方法保留的细节最丰富。

五、结束语

通过目视评价及统计分析可见,数学形态学方法进行去薄云处理是可行的,并且在选取合适的结构元素,特别是构造广义结构元素后利用数学形态学处理薄云,可以更好地保持处理区域的细节,效果更佳。但本文只根据试验影像的特点对结构元素进行了选取,而这种结构元素并不适合所有影像,在实践中应针对特定的影像选取合适的结构元素进行薄云处理,才能取得理想效果。因此,利用本文提出的方法进行薄云处理过程中,结构元素的选取仍在探讨之中,需要进一步深入研究。

[1] 朱锡芳,吴峰,孙燕滨.基于Mallat算法遥感图像去云雾处理的改进方法 [J].遥感学报,2007,11(2)：241-246.

[2] GAO B C,KAUFMAN Y J,HAN W,et al.Correction of Thin Cirrus Path Radiance in the 0.4-1.0μm Spectral Region Using the Sensitive 1.375μm Cirrus Detecting Channel[J].Journal of Geophysical Research,1998,103 (D24)：32169-32176.

[3] ZΗANG Y.A NewMergingMethod and Its Spectral and Spatial Effects[J].IntJ Remote Sensing,1999,20(10)：2003-2014.

[4] 赵忠明,朱重光.遥感图像中薄云的去除方法[J].环境遥感,1996,11(3)：195-199.

[5] 吴传庆,王桥,杨志峰.基于混合像元分解的水体遥感图像去云法[J].遥感学报,2006,10(2)：34-41.

[6] 李月臣,陈晋,刘春霞,等.一种除去遥感影像薄云雾的方法[J].成都理工大学学报：自然科学版,2006, 33(1)：58-63.

[7] 曹爽,李浩,马文.基于数学形态学的遥感影像薄云处理方法[J].地理与地理信息科学,2009,25(4)：30-33.

[8] 赵春晖,李兵,惠俊英.一种适于图像噪声平滑的广义形态滤波器[J].哈尔滨工程大学学报,2000,21(2)：55-59.

[9] 曹爽.高分辨率遥感影像去云处理研究[D].南京：河海大学,2006.

[10] GONZALEZ R C,WOODS R E,EDD INS S L.数字图像处理：Matlab版[M].阮秋琦,等译.北京：电子工业出版社,2005.

Removing Thin Cloud Arithmetic Based on GrayMathematic M orphology for Remote Sensing Images

CAO Shuang,YUE Jianping,MA Wen

0494-0911(2010)12-0054-04

P237