双基地制导雷达目标定位的分坐标融合算法*

(空军工程大学 导弹学院，陕西 三原 713800)

1 引 言

近年来，随着电子战技术的飞速发展，“四大威胁”(隐身目标、综合性电子干扰、低空超低空突防和反辐射导弹)的出现使得雷达面临着日益严重的生存危机。为了对付日趋成熟起来的“四大威胁”的挑战，双基地雷达获得重视[1-3]。

对于双基地制导雷达目标定位跟踪问题已有文献进行了一些研究[4-6]，目前常用的方法包括加权最小二乘和线性最小二乘方法等，但主要还是通过直接解算目标在坐标系的定位点而进行定位跟踪分析，由于目标坐标的相关性,使得数学分析比较复杂。

2 模型建立

2.1 距离和参数航迹模型

假设发射站T站址为(X1,Y1,Z1)，接收站R站址为(X2,Y2,Z2)，接收站测得发射站传送的通过目标的脉冲与时间的乘积为距离和Ri(i=1,2,3,…,n)，空间目标在t0时刻的位置为(x0,y0,z0)，由于制导雷达扫描速度达到每秒10～15帧，可假设目标匀速直线飞行，其速度为(Vx,Vy,Vz)，则有目标状态模型：

(1)

目标距离和模型：

(2)

其中：

ai=(xi-X1)2+(yi-Y1)2+(zi-Z1)2，
bi=(xi-X2)2+(yi-Y2)2+(zi-Z2)2。

将式(2)两端四次方后整理可得到：

(3)

假设式(1)中t0=0，代入式(3)整理，提取可观测参量序列，得到以下矩阵：

(4)

其中：

k1=c2，k2=4cd，k3=4d2，

k4=-2[(x0-X1)2+(x0-X2)2+(y0-Y1)2+

(y0-Y2)2+(z0-Z1)2+(z0-Z2)2]，

k5=-4[(2x0-X1-X2)Vx+(2y0-Y1-Y2)Vy+

(2z0-Z1-Z2)Vz]，

令：

c=(X2-X1)(2x0-X1-X2)+

(Y2-Y1)(2y0-Y1-Y2)+

(Z2-Z1)(2z0-Z1-Z2)

d=(X2-X1)Vx+(Y2-Y1)Vy+(Z2-Z1)Vz

在观测得到距离和序列的同时，也可得到角度的观测序列，即方位角序列和俯仰角序列。进一步建立航迹模型，可得到速度的方向。

2.2 角度参数航迹模型

测量目标方向为(li,mi,ni)，li=cosεisinβi，mi=cosεicosβi，ni=sinεi，其中，εi为俯仰角，βi为方位角，目标速度方向：l=cosεsinβ，m=cosεcosβ，n=sinε，则有：

VX=Vl，VY=Vm，VZ=Vn

(5)

接收站测量模型为

(6)

利用参量最小二乘法[7]：

Δ=

(7)

令：

将上式分别对(R1mi-RT)以及l、m、n求偏导并令其等于0，令：

T=diag(t1-t0,…,tn-t0)

通过整理，可得到目标速度方向的估计向量：

(8)

同理，利用发射站测得的俯仰角和方位角的观测序列，可以得到目标的速度方向的估计向量。比较归一化后的目标方向向量，如果该估计向量是相同的，可以判定为同一目标；如果该向量不同，则可判定为不同目标，即该算法适用于多目标跟踪。

2.3 参数航迹融合模型

通过对距离和和角度的参数航迹融合，得到了目标速度的大小和方向两组参量的估计值。由此，将这两组参量进一步联合解算，可以对目标进行定位，得到目标相对于参考坐标系的位置序列(xi,yi,zi)，i=1,2,3,…,n。

根据式(4)中的k1、k2、k5，可以得到目标的初始定位点(x0,y0,z0)。

通过整理，可以得到：

(9)

由于发射站与接收站都在地面，而目标在空中，那么，z0>0，其中，发射站T站址(x1,y1,z1)，该式左端的方阵为非奇异矩阵，可求逆，可得到(x0,y0,z0)，再通过式(1)，可以得到目标的位置序列(xi,yi,zi)，即：

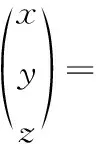
(10)

由此，可对目标进行定位及跟踪。

3 误差分析及算法仿真

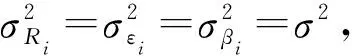
3.1 距离和参数航迹模型仿真

该模型是假设目标匀速直线飞行，速度大小不变，通过增大白噪声的标准差来观测真实值与估计值的偏差。图1为仿真结果。

图1 不同噪声标准差的速度大小估计值与真实值的比较

仿真结果表明，估计值随着噪声标准差的增大而与真实值的偏差逐渐增大。

3.2 角度参数航迹模型仿真

该模型是假设目标匀速直线飞行，速度方向不变，通过增大噪声的标准差来观测真实值与估计值的偏差。图2为仿真结果。

图2 不同噪声标准差的速度方向估计值与真实值的比较

仿真结果表明，目标速度方向向量的估计向量与真实向量的偏差随着噪声标准差的增大而逐渐增大。

3.3 参数航迹模型仿真

该模型是利用前两个实验得到的速度大小和方向，解算出目标的位置序列，加入噪声后，可得到每个坐标点偏差的方差，即可算出GDOP。同理，可解算出SWLS算法的GDOP，通过增大噪声的标准差来比较两种算法。

图3 不同噪声标准差的分坐标参数航迹融合算法与SWLS算法的GDOP比较

仿真结果表明，两种算法的GDOP都随标准差的增大而增大，而分坐标参数航迹融合算法不受系统误差的影响，其GDOP相对小于SWLS算法。

4 总 结

根据距离和的观测序列建立参数航迹模型，可以得到目标飞行速度的大小；根据角度的观测序列建立参数航迹模型，可以得到目标飞行方向；对得到的参数进一步参数融合，可以得到目标在坐标系的位置序列。该方法只需选择常用的直角坐标系，而不需要混合坐标系的变化。MATLAB仿真比较验证了该方法的有效性和优越性。该算法是在纯方位目标定位跟踪研究的基础上利用制导雷达是有源定位的这个优点，利用距离和这个测量序列，解算出了单纯利用纯方位无法解算的目标速度大小，利用这点彻底地解算出了目标的位置序列。该算法很好地解决了双基地制导雷达的目标跟踪问题，还解决了多目标探测问题，当测得目标飞行速度的大小或方向不同时，可以判定为多目标，因此可以对多目标进行跟踪。该方法丰富了目标定位跟踪理论，具有重要的理论和实践意义。

参考文献：

[1] 何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2008.

HE You,XIU Jian-juan,ZHANG Jing-wei,et al. Rader Data Processing With Applications[M]. Beijing:Publishing House of Electronics Industry,2008.(in Chinese)

[2] 杨振起,张永顺，骆永军.双(多)基地雷达系统[M].北京:国防工业出版社,2001.

YANG Zhen-qi,ZHANG Yong-shun，LUO Yong-jun. Bistatic Multistatic guidance radar systems[M]. Beijing:National Defense Industry Press,2001.(in Chinese)

[3] Bassem R Mahafza.雷达系统分析与设计[M].2版.北京:电子工业出版社,2008:338-379.

Bassem R Mahafza.Radar Systems Analysis and Design Using MATLAB[M].2nd ed.Beijing:Publishing House of Electronics Industry,2008: 338-379.(in Chinese)

[4] 刘军,杨宏文,郁文贤.优化的多基地雷达线性最小二乘定位方法[J].电光与控制, 2005，12(3):15-18.

LIU Jun,YANG Hong-wen,YU Wen-xian. Optimized linear least square method for target locating in multistatic radar system[J]. Electronics Optics and Control,2005，12(3):15-18.(in Chinese)

[5] 彭芳,左继章,吴军. 非线性最小二乘算法在双基地雷达目标定位中的应用[J].火力与指挥控制,2009,34(8):101-104.

PENG Fang,ZUO Ji-zhang,WU Jun. The Application of Nonlinear Least Square Estimation Algorithm to Bistatic Radar System's Target Location[J]. Fire Control and Command Control, 2009,34(8):101-104.(in Chinese)

[6] 朱永文,娄寿春,韩小斌.双基地雷达测向交叉定位算法的误差模型[J].火力与指挥控制，2007,32(6):51-53.

ZHU Yong-wen,LOU Shou-chun,HAN Xiao-bin. The Error Model of Cross Locating Algorithm for Bistatic Radar Direction Finding[J]. Fire Control and Command Control, 2007,32(6):51-53.(in Chinese)

[7] 刘进忙,姬红兵,董红波.基于红外单站的航迹跟踪方法[C]//第八届全国信号与信息处理联合学术会议论文集.珠海：陕西省图像图形学会，2009：61-63.

LIU Jin-mang,JI Hong-bing,DONG Hong-bo.The Method of track follow based on infrared single station[C]//Proceedings of the Eighth Conference on Signal and Information Processing.Zhuhai: Graph and Imaging Association of Shaanxi Province,2009：61-63.(in Chinese)