多径效应对信号接收及方向测量的影响
2010-09-26
(空军航空大学,吉林 长春 130022)
1 引 言
电磁波在空间传播中由于受到多径效应的影响,测向天线通常接收到的是直射波与由建筑物、树木等障碍物导致的反射、衍射和散射波的叠加,这些电磁波虽然频率相同,调制方式一样,但由于方向、多普勒频移和空时特性的差异[1],叠加后必然会造成接收信号的失真从而导致测向误差,这种误差虽然不能通过测向体制或算法的改进予以完全消除,但对不同测向体制有着不同的影响,因此研究多径效应针对具体测向体制造成的测向误差十分重要。
文献[2]采用信号叠加法对多径导致的干涉仪体制测向误差予以分析,建立了多径传播的二径模型,但其假设反射点在收发天线连线上,这就造成多径对方位角测量没有影响,与实际不符。文献[3]在二径模型的基础上,假设第二个反射点在收发天线连线外,建立了三径模型,并采用场强矢量叠加法对测向误差进行分析,但没有针对具体的测向体制,对实际的测向应用没有指导意义。文献[4]将单个多径分量用更符合实际情况的多径簇形式来描述,分析了接收天线为线阵时,多径对相关法测向体制造成的测向误差,但载机侦察平台受到体积等的限制,一般采用圆阵[5]。本文结合地空链路的实际情况,加入机身反射分量,将多径传输建模为四径模型,并考虑多普勒效应的影响,对发射信号、直射接收信号和多径接收信号进行仿真比较;采用信道椭圆模型[6]将单一方向多径分量建模为相同时延的多径簇,并推导了二维线阵和圆阵的输出响应矢量;对多径效应造成的机载L阵干涉仪和圆阵相关法测向的二维(方位角和俯仰角)测向误差进行了仿真分析。
2 L阵和圆阵测向误差分析
对机载平台测向而言,为了得到目标的方位和俯仰信息,一般采用L阵或圆阵的天线阵排列形式,通过不同天线测量目标辐射信号的相位信息,进而确定目标方向。
2.1 机载L阵相位干涉仪测向体制误差
由于一维干涉仪只能测量辐射源的方位角,且存在无法区分基线对称方向的缺点,因此机载侦察测向设备往往采用二维干涉仪测向体制,即在载机平台上配置3根天线A、O′、B,构成一个两基线相互垂直的二维相位干涉仪,如图1所示。

图1 机载L阵的几何示意图Fig.1 Airborne antenna L array geometrical sketch map
由图1中的几何关系可得到两基线的相位差分别为
(1)
式中,dx、dy分别为两基线的长度,λ为来波波长。由于基线和频率测量误差很小,可以忽略。令dx=dy=d,由式(1)可得到方位角α和俯仰角β的误差为
(2)
2.2 基于圆阵的相关法测向体制误差
由于噪声的不相关特性,可以对测向系统接收信号进行相关处理[5],设天线阵形式为N元均匀圆阵,其圆心位置为坐标轴原点,如图2所示。
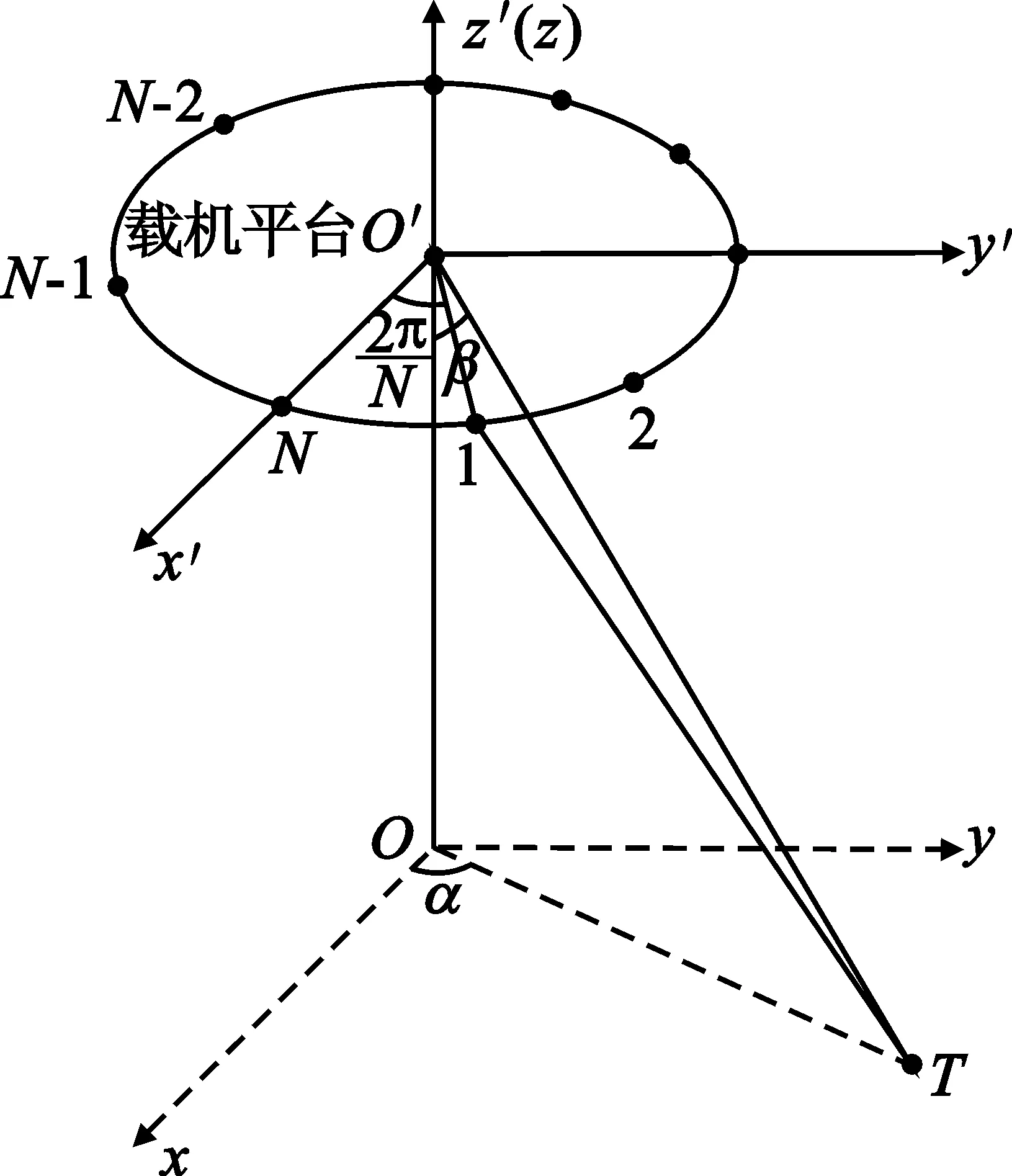
图2 机载圆周阵列的几何示意图Fig.2 Airborne antenna circular array geometrical sketch map
第i个天线的接收信号可表示为
xi(t)=s(t)exp{-j[kRsinβcos(α-γi)]}+ni(t)
(3)
式中,i=1,2,3,…,N,s(t)为发射信号,k=2π/λ,R为圆阵半径,γi=2π(i-1)/N,α为来波方位角,β为俯仰角,ni(t)为噪声信号。设不同天线接收信号之间、噪声之间以及接收信号和噪声之间是统计独立的,则不同天线接收信号的互相关函数可表示为

exp{-jkasinβ[cos(α-γi)-cos(α-γi+1)]}
(4)
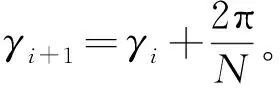
(5)
式中,i=1,2,3,4,5。为简便起见,在分析方位角误差时,假设俯仰角无误差,反之亦然。由式(5)可得到方位角α和俯仰角β的误差为
(6)
式中,i=1,2,3,4,5。
3 多径效应信号分析
在实际的测向过程中,信号受到多径效应的影响,接收到的信号不只是来自目标辐射源,还包括由于环境因素造成的多径反射导致的干扰信号,并且雷达部署的地形环境一般都比较复杂,高山、丘陵、森林、地面高大建筑等都可能对雷达发射的信号形成反射,进而对测向结果造成影响。
3.1 地空多径效应模型
机载测向设备对地面辐射源进行测向时,接收的辐射源电磁波除直射路径和地面反射路径外,还应包括远端障碍物(如:高山、丘陵等)和机体金属表面的反射效果,所建立的多径传输模型如图3所示。

图3 目标辐射信号多径示意图Fig.3 Target radiant signal multipath transmission sketch map
设辐射源发射信号为[7]
st(t)=AtGtft(α,β)exp(j2πfct)v(t)
(7)
式中,At为发射信号幅度,Gt为发射天线增益,ft(α,β)为发射天线方向图函数,fc为载波频率,v(t)为调制信号,则图3中直达波和3条反射波信号可分别表示为
sr0(t)=AtGtft(α,β)exp(j2πfc(t-tr0)+
2πf0t)v(t-tr0)fr(α,β)Gr
sr1(t)=AtGtR1ft(α1,β1)exp(j2πfc(t-tr1)+
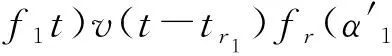
sr2(t)=AtGtR2ft(α2,β2)exp(j2πfc(t-tr2)+
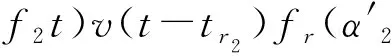
sr3(t)=AtGtR3ft(α3,β3)exp(j2πfc(t-tr3)+

(8)
式中,R1、R2、R3为3条反射波的反射系数;tr0、tr1、tr2、tr3为直达波和3条反射波的时延,可由图3中的几何关系计算得到;f0、f1、f2、f3为多径来波的多普勒频移,可表示为[1]

(9)
式中,c为光速,v为载机速度,εn为第n条入射波方向和载机运动方向夹角。
设干涉仪测向接收机完成一次采样处理时间为tc,当tc 实际情况中,信号的多径传播以多径簇的形式出现[6],用信道椭圆模型来分析,如图4所示。模型中所有椭圆都是共焦的,发射器Tx和接收器Rx位于椭圆的焦点上,对每一个椭圆上的反射波,它们具有相同的路径传播长度(时延相等),但是,它们各自的入射角不同,因此由接收器Rx移动引起的相应多普勒频率也是不同的。 图4 描述多径传播的椭圆模型Fig.4 Ellipse model of describing multipath transmission 对应每一个椭圆上的一簇反射波,假设其中心方位角为αn,分布在角域宽度为δ的范围内,中心俯仰角为βn,分布在角域宽度为σ的范围内,则第n个椭圆反射信号在第l个阵元上的输出可表示为 (10) 式中,k为第n个多径簇反射波的数量。 设有N根接收天线,接收矩阵可表示为X(t)=[x1(t),x2(t),…,xN(t)]T,则天线阵接收端信号的自相关矩阵R(t)可表示为[9] (11) 当只有单一信号入射时,自相关矩阵R(t)的第(m,n)个元素rmn(m≠n)可表示为 (12) 其中: C=AtGtft(α,β)exp(j2πfc(t-tr0)+2πf0t)v(t-tr0)Gr 在多径簇入射的情况下,阵列输出的自相关矩阵R1(t)的第(m,n)个元素r1mn(m≠n)可表示为 (13) 其中: Y=AtGtRPexp(j2πfc(t-trP)+2πfPt)v(t-trP)Gr 显然,多径簇的根数、角域范围等因素将直接影响两个自相关矩阵之间的差别,进而对相关法测向产生影响。 从图5中可以看出,仅存在直射路径时,信号在时域上除延迟和衰减外,各脉冲幅度仍然相等;频域上由于受到多普勒效应的影响,其频带展宽,谱峰出现平移,但形状基本没有发生变化。在多径的情况下,各信号经过延迟衰减后叠加在一起,各脉冲幅度变得参差不齐,信号频谱除更大的展宽外,其形状发生了变化。 由于L阵相位干涉仪和相关法测向本质上都是通过测量相位来获取目标方向的,发射信号、仅有直射路径的接收信号和多径情况下的接收信号相频变化如图6所示。从图6中可以看出,直射路径的相位仍然具有周期性,只是由于时域的延迟和多普勒频移造成相位周期和形状发生了改变,而在多径的情况下,相位谱没有任何规律,并且其变化速率明显增大,这必然对相位法测向产生影响。 (a)发射信号波形 (b)直射接收信号波形 (c)多径接收信号波形 (d)发射信号频谱 (e)直射接收信号频谱 (f)多径接收信号频谱 (a)发射信号 (b)仅有直射路径的接收信号 (c)多径情况下的接收信号图6 发射、接收信号相位谱变化对比图Fig.6 The phase spectrum contrast of transmission signal and receiving signal 上述仿真条件不变,在图3所示坐标系中,载机平台天线O的坐标为(0,0,8 000),天线A的坐标为(10,0,8 000),天线B的坐标为(0,10,8 000),l=250 km,c0=50 km,d=150 km。当λ=1 m、α=90°、β=80°时,根据式(2)可得到俯仰角和方位角的误差曲线如图7和图8所示。 图7 多径条件下干涉仪方位角测向误差Fig.7 Azimuth measurement error of phase interferometer in multipath condition 从图7和图8中可以看出,测向误差的方差较大,但其均值较小,这是因为多径传播具有很大的随机性,这就造成测向误差围绕真实来波方向上下波动,在某一采样点上,可能会出现较大的测向误差,因此,可以取尽量多的采样点测量值进行平均处理,这样可以有效减少多径误差的影响。另外,多径造成的俯仰角测量误差要大于方位角测量误差,这是因为反射点在收发天线连线上的多径反射波对方位角测量是没有影响的,但几乎所有的多径波都对俯仰角测量有影响。 图8 多径条件下干涉仪俯仰角测向误差Fig.8 Pitch angle measurement error of phase interferometer in multipath condition 设接收天线为五元均匀圆阵,圆周半径a=0.5 m,λ=1 m,来波中心方位角α0=30°,俯仰角β0=80°,每个多径簇射线数量为20根,射线来波方向和能量在各射线上均匀分布,进行500次蒙特卡洛(MC)试验,其角域扩展与测向误差变化曲线如图9所示。上述仿真条件不变,方位角域扩展范围δ=±5°,俯仰角域扩展范围σ=±5°,其多径簇射线数量与测向误差变化曲线如图10所示。 图9 多径簇角域扩展对相关法测向误差的影响Fig.9 Influence of angle spread of the multipath cluster on the direction finding measurement error with correlation method 图10 多径簇射线数量对相关法测向误差的影响Fig.10 Influence of radial number of the multipath cluster on the direction finding measurement error with correlation method 从图9中可以看出,随着多径簇角度扩展的增加,测向误差是快速增大的,这是因为角域扩展越大,来波多径簇可能和真实来波方位发生较大的偏移,会对来波多径簇中心估计产生大的影响。从图10中可以看出,随着单个多径簇射线数量的增加,测向误差是减小的,这是因为仿真中假设多径簇的射线数是均匀分布的,随着射线数量的增加,可以在一定的误差范围内,反映出多径簇的中心来波角度。另外,多径簇对俯仰角测量的影响要大于方位角,这和图7和图8中的分析是一样的。 多径传播造成接收信号特性相对于发射信号发生变化,进而影响到参数测量,引起测向误差。本文通过建立地空电磁波多径传输模型对L阵相位干涉仪和圆阵相关法测向误差进行了定性和定量的分析,对相位干涉仪而言,主要是不同到达时间的多径信号相互叠加造成相位差测量误差而引起测向误差,其误差大小主要与辐射源和反射物的位置有关;对相关法测向来说,主要是受到多径簇产生的空间角度扩展造成相关系数计算出现误差而引起测向误差,其误差主要和空间障碍物数量和分布有关,且对两种测向体制,多径对俯仰角测量的影响都要大于方位角。由于多径来波是经过不同的传播距离、不同的传播方向随机的在接收端进行空间合成,因此,可通过以下3种方法来降低多径传播对测向结果的影响: (1)缩短接收机采样处理时间。当干涉仪测向接收机完成一次采样处理时间小于直射波和反射波到达测向天线的时间差,则测得的方向仅为直射波方向; (2)通过设计特殊的测向天线,降低反射波接收幅度。比如,在测向天线下方安置屏蔽地面反射波的抑径板或者抑径圈可以有效地降低二径传播造成的测向误差; (3)对信道环境进行评估,剔除掉恶劣信道环境下的测量结果,对剩余测量值进行平均。 参考文献: [1] 胡凯.多径衰落信道的典型特征分析及仿真研究[J].电子对抗,2010,33(1):42-47. HU Kai.Typical Characters Analysis and Simulation Research on Multi-path Fading Channels[J].Electronic Warfare,2010,33(1):42-47.(in Chinese) [2] 刘亚平.多径传播对反反舰导弹相位干涉仪测角影响的建模与仿真[D].长沙:国防科技大学,2007:18-22. LIU Ya-ping.Modeling and simulation of multipath effects on passive radar seeker[D].Changsha: National University of Defense Technology,2007:18-22.(in Chinese) [3] 谢飞,张忠臣,张鹏,等.多径效应对测向误差的影响[J].电子测量技术,2010,33(1):29-31. XIE Fei,ZHANG Zhong-chen,ZHANG Peng,et al.Influence on direction finding error by multipath effect[J].Electronic Measurement Technology,2010,33(1):29-31.(in Chinese) [4] 王玉玲,赵小芳.基于多径分量簇的信号处理技术研究[J].无线电通信技术,2007,33(6):30-32. WANG Yu-ling,ZHAO Xiao-fang.Research on Signal Processing Based on Multi-path Component Clusters[J].Radio Communications Technology,2007,33(6):30-32.(in Chinese) [5] XUN Yang,CUI Zhang-zhong.Two-dimensional Circular Array Real-time Phase Interferometer Algorithm and Its Correction[C]//Proceedings of 2nd International Congress on Image and Signal Processing.Tianjin:IEEE,2009:1-5. [7] Bassem R Mahafza,Atef Z Elsherbeni.雷达系统设计MATLAB仿真[M].朱国富,黄晓涛,等,译.北京:电子工业出版社,2009:105-106,232-249. Bassem R Mahafza,Atef Z Elsherbeni. MATLAB Simulations for Radar Systems Design[M].Translated by ZHU Guo-fu,HUANG Xiao-tao,et al.Beijing:Publishing House of Electronics Industry,2009:105-106,232-249.(in Chinese) [8] 王晨阳,董文锋,王正国.反辐射导引头在多信号环境下的定向能力分析[J].空军雷达学院学报,2009,23(6):423-425. WANG Chen-yang,DONG Wen-feng,WANG Zheng-guo.Analysis of ARPRS Direction Finding Under the Multi-signal Environment[J].Journal of Air Force Radar Academy,2009,23(6):423-425.(in Chinese) [9] 王月瑜,郭黎利.三维接收天线阵列信道模型下的空域相关性[J].计算机工程,2008,34(12):9-11. WANG Yue-yu,GUO Li-li.Spatial Correlation in Three-dimensional Receiver Antenna Array Channel Model[J].Computer Engineering,2008,34(12):9-11.(in Chinese)3.2 信号传播多径簇模型

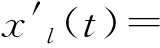
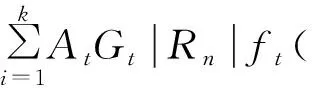
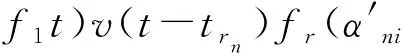
3.3 多径簇下接收阵列相关性分析
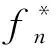


R0=14 仿真分析
4.1 多径对接收信号影响仿真

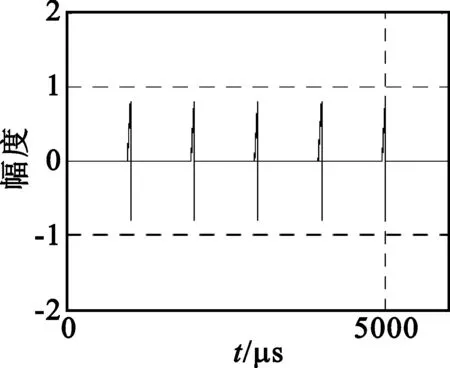


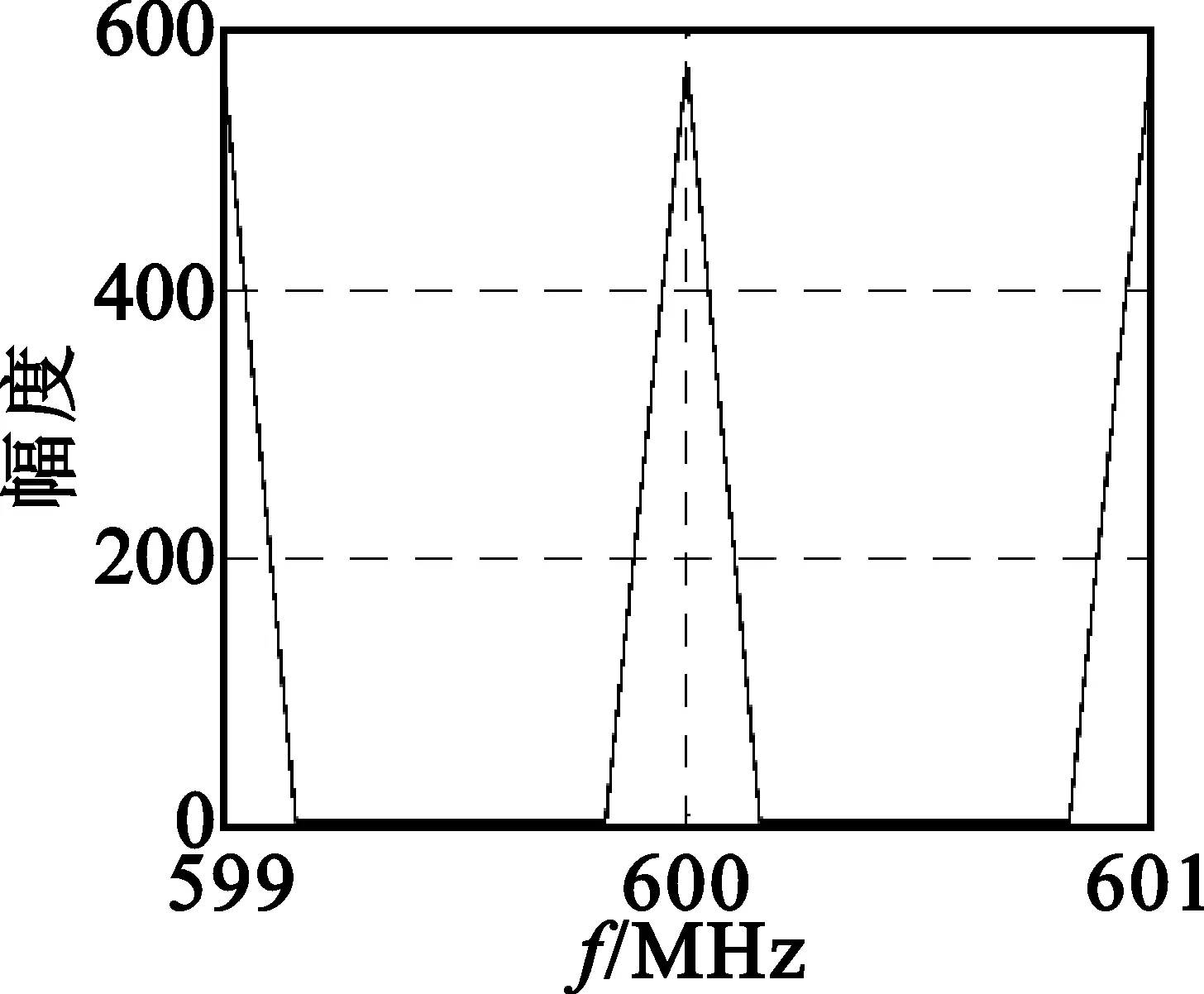





4.2 多径对干涉仪测向误差仿真
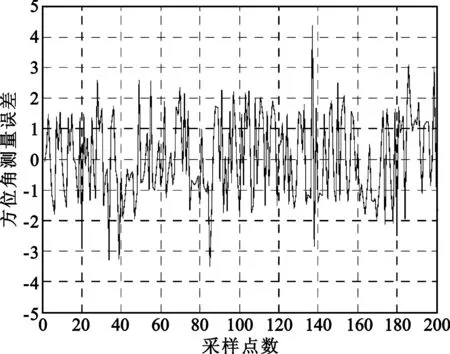

4.3 多径对相关法测向误差仿真


5 结 论
