分形植物的模拟仿真及其分形维数的研究

邓永菊,王世芳＊,吴 涛

（1.湖北第二师范学院物理与电子信息学院,武汉430205;2.武汉工程大学理学院,武汉替换为 430073）

分形植物的模拟仿真及其分形维数的研究

邓永菊1,王世芳1＊,吴 涛2

（1.湖北第二师范学院物理与电子信息学院,武汉430205;2.武汉工程大学理学院,武汉替换为 430073）

基于分形物整体与局部的自相似性与自复制性的特征,采用随机线性迭代函数算法,利用计算软件mathematica 7.0成功模拟了蕨叶和分形树的生成过程;另外还采用计盒数法,通过软件编程分别计算出蕨叶和分形树的分形维数分别为1.45和1.52,所得结果与在二维空间中分形物体的分形维数在1～2之间的结论相一致.

分形;计盒数法;随机线性迭代函数算法;分形维数;mathematica 7.0

分形最初是由美国学者Mandelbrot[1]首先提出的,分形理论的真正发展起来才30余年,在这期间得到了突飞猛进的发展,并引起了越来越多的学者和研究者的注意和兴趣,极大地推动了非线性学科的发展.分形几何理论的应用己遍及生物学、物理、化学、材料科学、图像学、生物与医学、油藏、土壤等自然科学领域以及经济、人文等社会科学领域,展现了令人瞩目的应用前景,解决了许多传统理论和方法无法解决的问题,为现代科学研究提供了新的手段[2-5].欧氏几何认为空间的维数是整数,其描述的图形的边界都是规则的且可以用一定的解析式表示,例如直线、平面、球或立方体等,他们的维数分别为1维、2维和3维.对于自然界中存在大量分形物体 ——枝叶茂盛的树木、肥沃的土壤、弯弯曲曲的海岸线、纵横交错的血管,令人眼花缭乱的满天繁星、千姿百态的云彩、各种各样的多孔介质等等,它们的局部和整体存在统计意义上的自相似性,它们的维数也不再为整数,而是分数,我们称之为分维数.产生分形图形的方法有L系统、随机线性迭代函数系统、复分形图生成,粒子系统模型、随机插值法等等[4-9].其中L系统缺乏质地感或纹理感,以画线编程实现,编程难度大;复分形图通过逃逸时间算法画点来完成,画出的图象更具有艺术感,编程复杂;粒子系统模型和随机插值法均有编程难度大的缺点.近年来,虽有不少研究者基于L系统的植物图像进行了模拟仿真,大多数都是采用VC与VB语言编写的,编程工作量大,而且没有给出植物的分形维数[10-11];张峰刚[12]基于随机线性迭代函数系统（Iterated Function System,简称IFS）利用VC++编程模拟了分形树的生成,但是编程复杂且他们并没有计算出分形树的分形维数.本文利用Mathematica编程方便、简单,计算速度快等优点,采用随机线性迭代函数系统算法来生成植物的分形图形,并通过计盒数法分别计算出蕨叶和分形树的分形维数分别为1.45和1.52,所得结果与在二维空间中分形物体的分形维数在1～2之间的结论相一致[13-14].

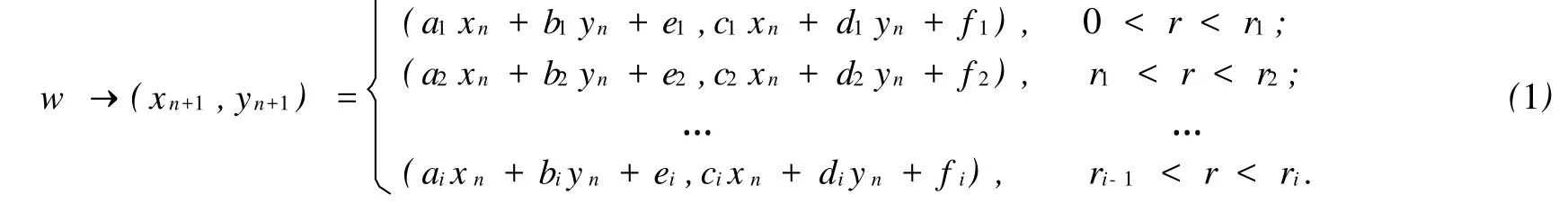
1 随机线性迭代函数算法

随机线性迭代函数系统最早是由 Hutchinson于1981年提出的[15],是分形几何学的一个重要分支.IFS是以仿射变换为框架,根据几何对象的整体与局部具有自相似结构,经过迭代而产生的.其基本思想为首先选定一个收缩变换的集合（即一个IFS代码）,然后从一个任意点开始,从集合中随机选择一个变换应用于该点,把它变换到另一点;再随机选择另一个变换并应用于新的点,再产生新的点;如此继续.所有这些点的集合,在屏幕上画出来的图形,被称为IFS的吸引子.仿射变换的数学表达式为[8,16]:

式中,w代表仿射变换;xn和yn是变换前图形的坐标值,xn+1和yn+1是变换后图形的坐标值;ai,bi,ci,di,ei,fi是仿射变换系数;ri为仿射变换被调用的概率.

2 分形蕨叶的模拟

首先产生[0,1]均匀分布的随机数 r,以下面的分段函数形式进行迭代,迭代次数为n=50000,起始点位置 x0=0,y0=0.

根据方程（1）,可以确定分形蕨叶的仿射变换系数（即 IFS码）:算法与步骤为:

①生成[0,1]均匀分布的随机数r;

②分配四个仿射变换的概率空间,分别为[0,0.01],（0.01,0.08],（0.08,0.15],（0.15,1];

③判断随机数落入的概率区间,并调用相应的仿射变换所具有的 IFS码值,赋给相应的参数ai,bi,ci,di,ei,fi;

④根据仿射变换关系式（2）计算变化后的xn+1,yn+1,在（xn+1,yn+1）处画一点;

⑤循环执行步骤 ①～ ④,并将上次计算出的结果 xn+1,yn+1值作为这次的 xn,yn值参加计算.

根据上面算法利用mathematica 7.0编写程序代码,画出如下图1所示蕨叶的分形图.从图1中,我们看出由IFS码绘出蕨叶形象、逼真.

分形维数是定量表示自相似随机分形物体的最基本物理量,在实际工程中往往需要计算分形维数.下面我们通过计盒数法[1-4]确定图1中蕨叶的分形维数.较简单的测定分形生成物分形维数的方法是把所研究的区域划分为一定尺寸ε的正方形小格子,然后计算生成物所占的格子数 N（ε）.改变格子的大小ε,又得到一个新的 N（ε）值以此类推,最后就可以找到 N（ε）与ε之间存在一定的标度关系:

图1 蕨叶的分形图Fig.1 The simulation of fractral fern

由此看出,直线的斜率就是其分形维数.对分形图形或图像来说,分形维数表征了分形图形所蕴含信息的多少,因此分形维数的计算具有重要的意义.为了定量计算蕨叶的分形维数,需要在蕨叶图形上加网格,如图2所示.设每个网格（盒子）的边长为ε,边长的倒数δ=1/ε.图2（a）～ （e）每个盒子的边长分别为3/8,1/4,1/6,1/8,1/10,边长的倒数δ对应为8/3,4,6,8,10,然后分别数出每个网格中占有一个或一个以上点的盒子数目为N=7,15,27,39,58.以 lnδ为横坐标、lnN（δ） 为纵坐标画出这5个数据点,并采用最佳线性拟合的方式（其拟合直线方程式为 y=1.45x+0.69）,计算出拟合直线的斜率,即为蕨叶的分形维数Ds=1.45,如

图2 分形蕨叶的网格划分Fig.2 The grid of fractral fern with square grid superiposed

图3 分形蕨叶的分形维数Fig.3 The fractral dimension of fractral fern

图3所示.

3 分形树的模拟

设二维分形树以下面的分段函数形式进行迭代,迭代次数为 n=105,起始点位置 x0=0,y0=0.

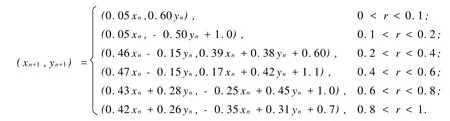
同样利用mathematica 7.0编写程序,模拟分形树的生成,如图4所示.

图4 分形树的生成Fig.4 The simulation of fractral tree

依照前面相同方法,用计盒法求出分形树的分形维数为Ds=1.52,如图5（a）-（d）及图6所示.

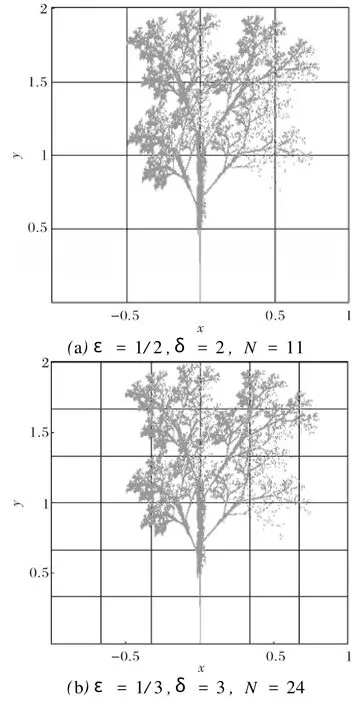
图5 分形树的网格划分Fig.5 The grid of fractral tree with square grid superiposed

图6 分形树的分形维数Fig.6 The fractral dimension of fractral tree

5 小结

植物是自然界的重要组成部分,根据植物的形态结构与特征,植物的生长可以看作是植物细胞按一定的规律不断发育、分裂的过程,这种按某种规律分裂的过程可以近似地看作为递归、迭代过程,这与分形的产生极为相似.因此在这种意义上说,可以认为一种植物对应一个迭代函数系统.从蕨叶的生成和分形树的形成可以看出,由IFS绘出的分形图形具有无穷细微的自相似结构,能对客观事物作出准确的反映.本文利用数学软件Mathematica具有内容丰富、功能强大、操作方便简单、界面友好等突出优点,采用随机线性迭代函数系统算法成功地模拟了蕨叶以及分形树的生成,并分别计算了它们的分形维数为1.45和1.52,这与在二维空间中分形体的分形维数0

[1]Mandelbrot B B.The fractal geometry of nature[M].San-Franciso:Freeman,1982:23-57.

[2]谢和平,张永平,宋晓秋,等.分形几何—数学基础与应用[M].重庆:重庆大学出版社,1991.

[3]辛厚文.分形理论及其应用[M].合肥:中国科学技术出版社,1993.

[4]Kaye B H.分形漫步[M].徐新阳,康 雁,陈 旭,等译.沈阳:东北大学出版社,1994.

[5]孙 敏,马蔼乃,毛善君.3DGIS中树的表达与可视化的研究[J].计算机辅助设计与图形学学报,2001,10（13）:901-905.

[6]陈昭炯.基于L—系统的植物结构形态模拟方法[J].计算机辅助设计与图形学学报,2000,8（12）:571-574.

[7]孔 勇,璩柏青.L系统在植物形态模拟中的应用[J].农机化研究,2007（4）:136-138.

[8]孙博文.分形算法与程序设计—Visual C++实现[M].北京:科学出版社,2004.

[9]齐东旭.分形及计算机生成[M].北京:科学出版社,1994.

[10]袁 杰,刘大昕.基于L系统的植物图像计算机模拟[J].应用科技,2002,29（11）:4-46.

[11]郑 达,胡德婷,何兴恒.基于随机系统的三维分形树算法和实现[J].计算机应用,2007,27:100-103.

[12]张峰刚,颜国明,薛 青.三维树木的计算机模拟[J].仿真学报,2006（1）:407-413

[13]Yu Bo Ming,Li Jian Hua.Some fractral characters of porous media[J].Fractrals,2001（9）:365-372.

[14]Yu Bo Ming.Fractral character for tortuous streamtubes in porous media[J].Chin Phys Lett,2005,22（1）:158-160.

[15]Hutchinson JE.Fractal and self-similarity[J].Indiana Univ Math J,30:713-749.

[16]Enns R H,McGuire G C.Nonlinear Physics with Mathematica for Scientists and Engineers[M].Berlin:Birkhauser,2001:83-89.

Abstract:In this paper,based on the characteristic of self-similarity and self-replicability for ensemble or local of fractal,the fractral fern and the fractral tree are successfully simulated by means of random linear iterative iteration function algorithm by mathematica 7.0.Futhermore,the box counting method is applied to investigate the fractal structure and the fractal dimension for the fractral fern and the fractral tree are determined to be 1.45 and 1.52,respectively.This is consistant with the result of the fractral demension between 1 and 2 for two dimensions.

Key words:fractral;the box counting method;random linear iteration function algorithm;the fractal dimension;mathematica 7.0

Study on the simulation of fractral plant and fractral demension

DENG Yongju1,WANG Shifang1,WU Tao2
（1.School Physics and Electronic Information,Hubei University of Education,Wuhan 430205;2.School of Science,Wuhan Institute of Technology,Wuhan 430073）

O41

A

1000-1190（2010）04-0585-05

2010-07-08.

＊E-mail:flatime@sina.com.