自共轭四元数矩阵特征值和的界
2010-09-25吴雪莎
吴雪莎
(重庆电子工程职业学院,重庆401331)
自共轭四元数矩阵特征值和的界
吴雪莎
(重庆电子工程职业学院,重庆401331)
本文利用自共轭四元数矩阵迹与特征值的一些关系式,将求特征值和的界的问题转化为两个优化问题,得到自共轭四元数矩阵的部分特征值的界。设自共轭四元数矩阵有n个特征值,如果已知自共轭四元数矩阵的最小(最大)特征值,可以得到其前k(1≤k≤n)个最大(最小)特征值的和的上(下)界。
自共轭;特征值;界
对于特殊的四元数矩阵,我们知道自共轭四元数矩阵的右特征值一定为实数。本节将借助于自共轭四元数矩阵迹与特征值的一些关系,得到其部分特征值和的界。
引理1 设A为自共轭四元数矩阵,λ1(A),λ2(A),…,λn(A)为A的n个右特征值,则
引理2 设为自共轭四元数矩阵,λ1(A),λ2(A),…,λn(A)为A的n个右特征值,则
证明:设λ为A的右特征值,则Aα=αλ,从而
AAα=Aαλ⇒AAα=αλλ⇒A2α=αλ2⇒λ2为A2的右特征值。
又因为A为自共轭四元数矩阵,所以(A2)*=(AA)*= A*A*=(A*)2=A2
故A2为自共轭四元数矩阵。又由引理(1)可得

定理1 设为自共轭四元数矩阵,λ1(A),λ2(A),…,λn(A)为A的n个右特征值,则

且当且仅当λ1=λ2=…=λn时等号成立。

且当且仅当λ1=λ2=…=λn时等号成立。
证明1 由引理1,显然可得式(1)。
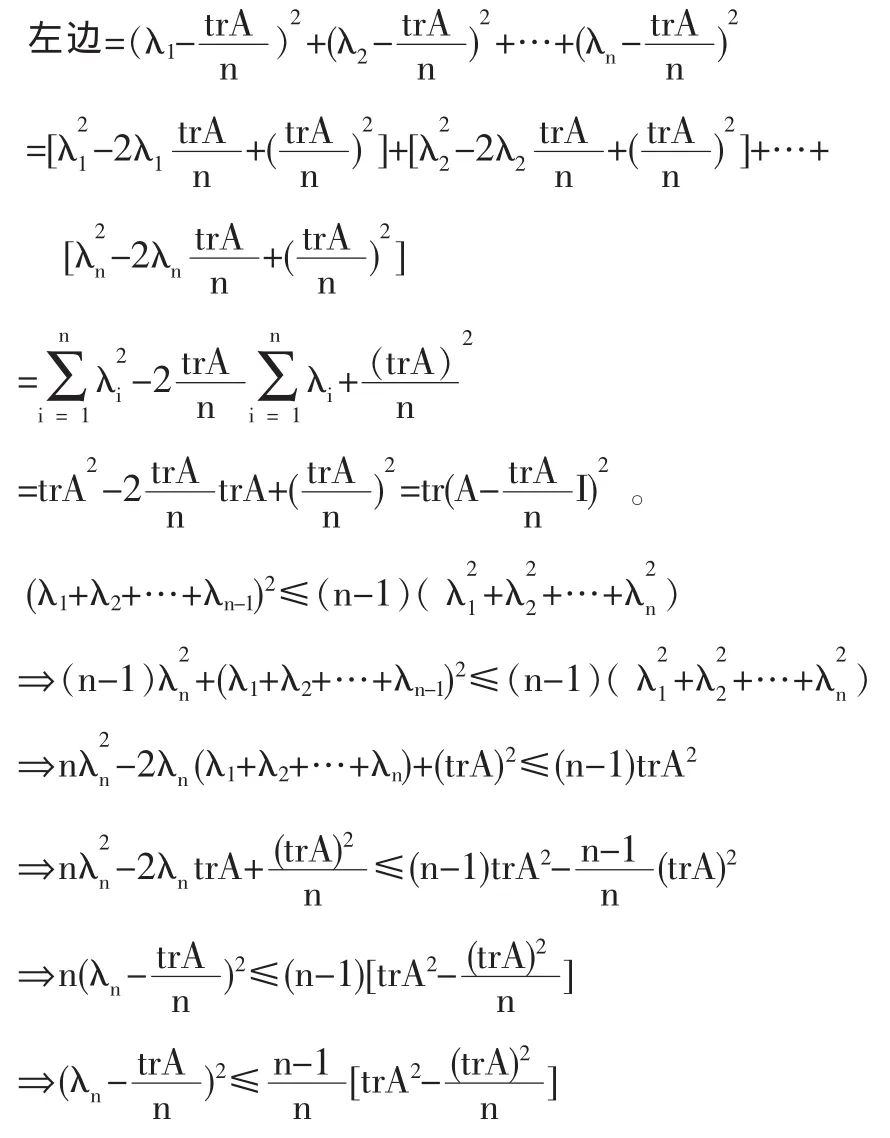
证明过程可仿照(3)的证明,显然可得。
上面的关系式表明可以定义集合
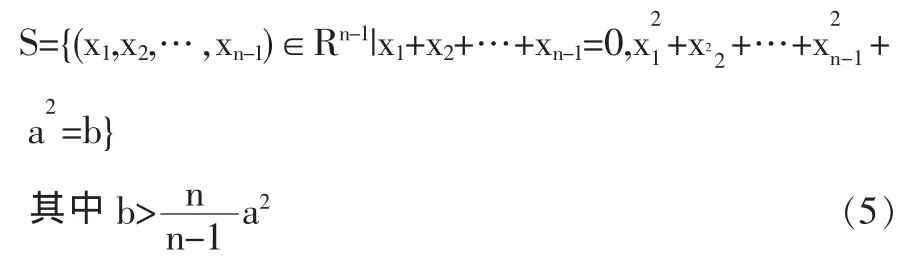
令f(x1,x2,…,xn-1)=x1+x2+…+xk
下面解决两个最优化的问题:
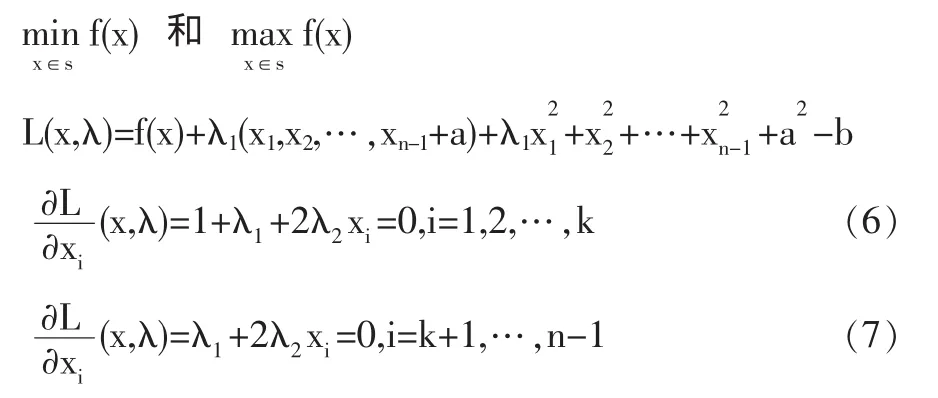
可以得到

所以

整理得
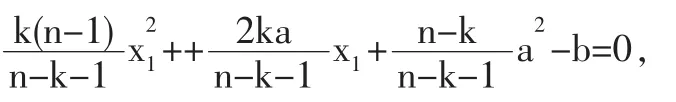
进而得到
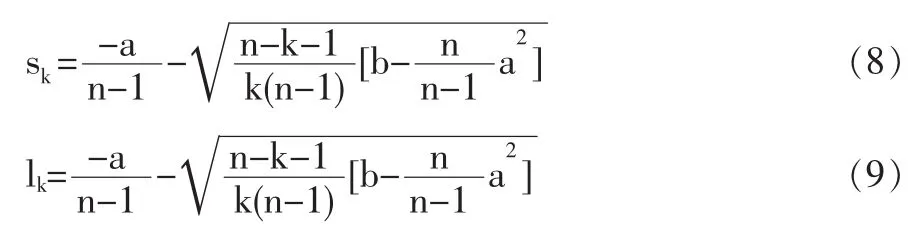
可以看出

因此,如果(x1,x2,…,xn-1)是拉格郎日函数L的稳定点,则

或者
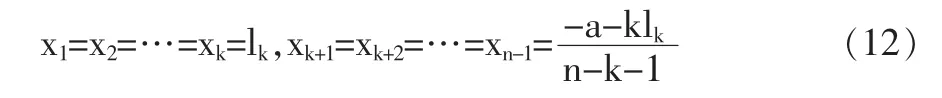
又

即得到

取x1=sk,那么由(10)得

因此x1-xk+1<0且λ2>0。
故Δ2L(x,λ)=2λ2I是正定矩阵。
f在式(11)给出的x点取得最小值,fmin=ksk。
现取x1=lk,由式(10),得
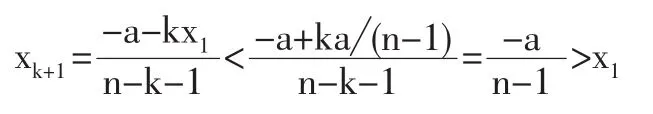
此时x1-xk+1>0且λ2<0,故2L(x,λ)=2λ2I是负定矩阵,fmax=klk。
因此有如下结论。
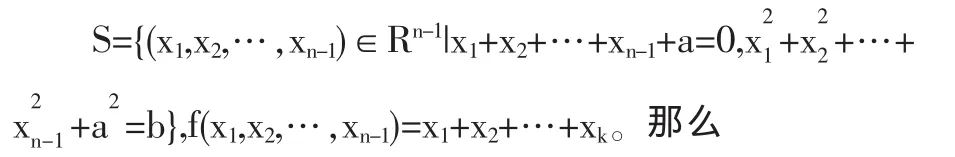

定理3 设λi(i=1,2,…n)是自共轭四元数矩阵A的右特征值,且λ1≥λ2≥…≥λn.如果λn已知,那么

且

其中


特别的,对于定理2,取k=1,有以下结论:
推论1设λi(i=1,2,…n)是自共轭四元数矩阵A的右特征值,且λ1≥λ2≥…≥λn.如果λn已知,那么

其中f(A)如式(18)。
注意:在式(19)和(20)中,我们看到给出了包含特征值的一个区间。这个区间可以不用计算A2就可以得到,因为

定理4 设λi(i=1,2,…,n)是自共轭四元数矩阵A的右特征值,且λ1≥λ2≥…≥λn≥0。那么

且
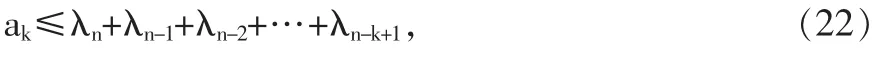
其中
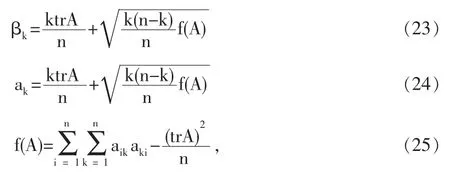
特别的,λ1≤β1,a1≤λn。
定理5 设λi(i=1,2,…,n)是自共轭四元数矩阵A的右特征值,且λ1≥λ2≥…≥λn。 如果λ1已知,那么
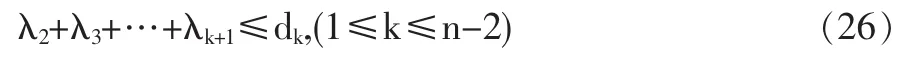
且

其中
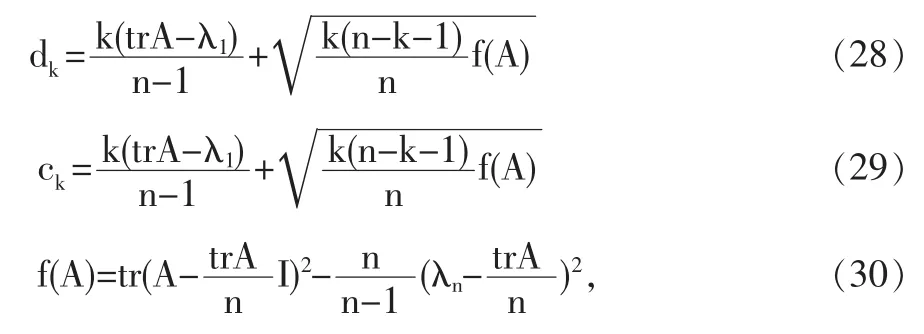
推论2设λi(i=1,2,…,n)是自共轭四元数矩阵A的右特征值,且λ1≥λ2≥…≥λn。 如果λ1已知,那么

且
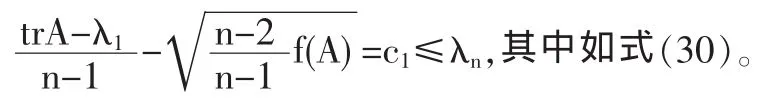
[1]曹重光.四元数自共轭矩阵的几个定理[J].数学研究与评论, 1988(08):346~348.
[2]FuZhen.Zhang.Quaternions and Matrices of Quaternions[J].Linear Algebra and its Applications.251(1997):21~57.
[3]李文亮.四元数自共轭矩阵迹的一些不等式 [J].长沙电力学院学报(自然科学版),1996(01):54~59.
[4]陈湘贇.四元数矩阵特征值的估计定理 [J].南京工程学院学报(自然科学版),2008(06):10~12.
[5]张树青.关于四元数矩阵之迹的几个定理 [J].数学研究与评论,1993(04):18~22.
[6]黄礼平.关于四元数矩阵迹的不等式[J].湖南数学年刊,1992 (03):409~454.
[7]曹重光.关于四元数自共轭矩阵迹的几个不等式 [J].数学杂志,1988(08):313~314.
[8]庄瓦金.四元数矩阵的特征值与奇异值不等式[J].数学进展, 1988(10):403~407.
责任编辑 郑 文
Bounds of the Sum of Self-conjugate Quaternion Matrix Eigenvalues
WU Xuesha
(Chongqing College of Electronic Engineering,Chongqing 401331,China)
In this paper,by use of the relation between eigenvalue and trace of self-conjugate quternion matrix,to solve the bound of sums of eigenvalues is changed into two optimization questions and we obtain the solutions.In addition,suppose a self-conjugate matrix have n eigenvalues,if its the minimum(maximum)is known,then the bound of sums of the first k(1≤k≤n)largest(smallest)eigenvalues can be achieved.
self-conjugate;eigenvalue;bound
O17
A
1674-5787(2010)03-0139-03
2010-04-20
吴雪莎(1983—),女,重庆市人,重庆电子工程职业学院人文素质部,助教。
