道路设计中回旋曲线的算法与画法

朱海鹏，王 伟

（沈阳市市政工程设计研究院，辽宁沈阳110015）

0 引言

城市道路和互通立交设计中，回旋线作为平曲线的缓和曲线得到广泛应用。目前大多数设计单位应用的计算机辅助设计软件AutoCAD，并没有回旋曲线类型对象，使得缓和曲线的设计绘图十分繁琐。本文结合作者多年的道路设计实践，对设计人员自定制回旋曲线的画法和算法进行探讨，并提出一种方便易用的定制方法。

1 回旋曲线的计算公式

早期道路设计为方便手工计算，回旋线计算一般采用近似公式。在计算机设计应用初期，通过对回旋线坐标公式的推导，可以采用多项式前5项计算。进入21世纪，计算机的运算速度大大提高，回旋线坐标完全可以采用高精度的计算通式。

回旋曲线的参数公式：

回旋线终点(SC)：A2=Ls×R （1）

回旋线上任一点：A2=Li×Ri（2）式（1），（2）中：A——回旋曲线参数；Li——任一点回旋线长度；Ri——任一点曲率半径。回旋曲线的坐标计算通式：

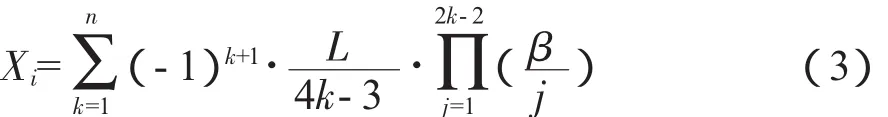
式（3），（4）中：Xi、Yi——回旋曲线任一点坐标，i、j、k、n 为正整数；

L——该点回旋线长度；

β——该点回旋曲线角。

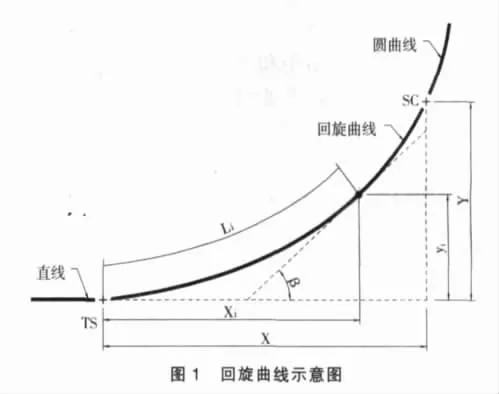
图1为回旋曲线示意图。

2 回旋曲线对象类型

分析一下道路平面线形设计，对中线的操作主要包括：（1）全程路线进行排桩号；（2）标注和导出逐桩坐标；（3）对平曲线特征点进行编号排序；（4）通过中线偏移生成路幅边线；（5）计算道路长度和关联的边线路缘石长度。中线作为道路平面对象模型的根对象，也是道路附属设施空间定位的主要参照，例如交通标志、路面标线、信号设施、给水排水管道等专业设计，均需通过道路中线来布设构造物。因此，回旋曲线对象作为道路平面线形的一个单元，必须与路线其它部分保持关联形成整体。

一种简单易行的办法，是采用AutoCAD的多段线对象绘制回旋曲线，最终将路线中全部的圆曲线、回旋线、直线单元连接成一条多段线，形成完整的道路中线，即可满足上述全部设计要求。多段线对象的 DXF类名为 LWPOLYLINE，ActiveX类名为AcDbPolyline，其特性是同一对象中可以包含直线段和圆弧段。应用这一特性，用多个圆弧段来模拟出回旋曲线，只要分段数目合理，顶点坐标计算精度足够，是完全可行的。研究表明，应用传统经验公式计算顶点坐标时，要满足工程精度要求需要细分百余段，大大增加了图形文件尺寸，而采用精确的计算通式，则十个圆弧段模拟的回旋曲线即可满足工程精度要求。

3 任意点坐标求解函数

计算机辅助设计软件AutoCAD内嵌了两种编程 语 言 ，Visual LISP和 VBA (Visual Basic for Applications)，其编辑编译环境内嵌于AutoCAD中，简便易学，已经为诸多设计人员所掌握，成为设计绘图的得力工具。下面是笔者用Visual LISP和VBA两种语言编写的横坐标求解函数。该函数采用前述计算通式，按照给定的循环次数，求解回旋线上任意点横坐标。注意，这里所说的横纵坐标，是回旋曲线的横距和纵距。

（1）Visual LISP语言编写的回旋曲线横坐标求解函数如下：

(defun vl_SpiralX(A B n/F1 F2 F3 J K LI XI)

(setq Li(*A(sqrt(*2.0 B))));计算点回旋线长度

(setq Xi 0.0)

(setq k 1)

(while(＜=k n)

(setq f1(expt-1(1+k)));通式第一项

(setq f2(/Li(-(*4 k)3)));通式第二项

(setq f3 1.0)

(setq j 1)

(repeat(-(*2 k)2)

(setq f3(*f3(/B(float j))));通式第三项

(setq j(1+j))

)

(setq Xi(+Xi(*f1 f2 f3)))(setq k(1+k))

)

Xi;返回横坐标

)

（2）VBA语言编写的回旋曲线横坐标求解函数如下：

Public Function vb_SpiralX(A As Double,B As Double,n As Long)As Double

Dim Li As Double,Xi As Double

Dim f1 As Double,f2 As Double,f3 As Double

Dim k As Long,j As Long

Li=A*Sqr(2#*B) '求解点回旋线长度

Xi=0#:k=1

Do While k＜=n

f1=(-1)^(k+1) '通式第一项

f2=Li/(4*k-3)'通式第三项

f3=1#

For j=1 To 2*k-2

f3=f3*(B/j)'通式第二项

Next

Xi=Xi+f1*f2*f3

k=k+1

Loop

vb_SpiralX=Xi'返回横坐标

End Function

函数参数：A为回旋曲线参数；B为求解点的缓和曲线角，单位为弧度；n为计算通式循环次数，一般取15。两个函数完成相同的工作，均返回坐标数值。实际应用中，回旋曲线分段数一般采用10的整数倍，以方便搜索曲线特征点。

4 生成回旋曲线

求得回旋曲线分段顶点坐标后，绘制回旋曲线的函数可以有多种编制方法。如果采用ActiveX方法成图，把坐标换算到世界坐标系比较方便；如果采用命令函数方式成图，可以充分利用导线的约束使用相对坐标。需要注意的是为保证全体线元的可连接，每条模拟回旋曲线的多段线都必须保证Z轴方向的一致。

图2是选择两条导线为约束条件时基本型回旋线的成图，其运行过程为：（1）选择第一条切线；（2）选择第二条切线；（3）输入圆曲线半径(R)；（4）输入第一条回旋线参数(A1)或长度(L1)；（5）输入第二条回旋线参数(A2)或长度(L2)；（6）指定平曲线标注位置。

5 结语

本文所述回旋曲线的算法和画法，同样适用于各种复合曲线。由于线形设计具有多样性和灵活性，设计人员掌握一种AutoCAD定制方法十分必要，大量交互和条件多变时采用逐个线元设计成图，数据条件齐备时通过读取数据文件自动生成全程路线和多条路线，对已经绘制完成的路线实现自动标注曲线元素表和输出路线数据到文件。如果图形和数据交换采用AutoCAD和Excel完成，势必极大提高设计质量和设计效率。笔者编制的道路设计软件包含了计算绘图一体化的线形设计模块，可以访问网站http://www.hpcad.com进一步了解。本文所述方式在多项大型工程设计中进行应用，效果良好。