基于谱线特征的MPSK调制识别

李少凯， 董 斌， 刘 宁

（第二炮兵指挥学院，湖北 武汉 430012）

0 引言

信号调制方式自动识别在通信侦察、电子对抗等方面均有重要意义。目前，常见识别方法有基于瞬时特征提取的算法；基于高阶累积量的算法；基于似然估计的算法等[1]。另外，也可将多种算法相结合以提高识别效率，如将高阶累积量和分形盒维数相结合[2]。由于MPSK的特性相似，采用上述算法的效果均不佳。选取BPSK、QPSK、OQPSK、8PSK、pi/4QPSK五种信号进行研究。

1 脉冲成形对信号特征的影响

信号进行Hilbert变换，得到复信号为：

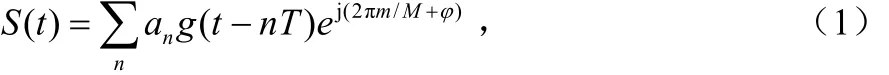
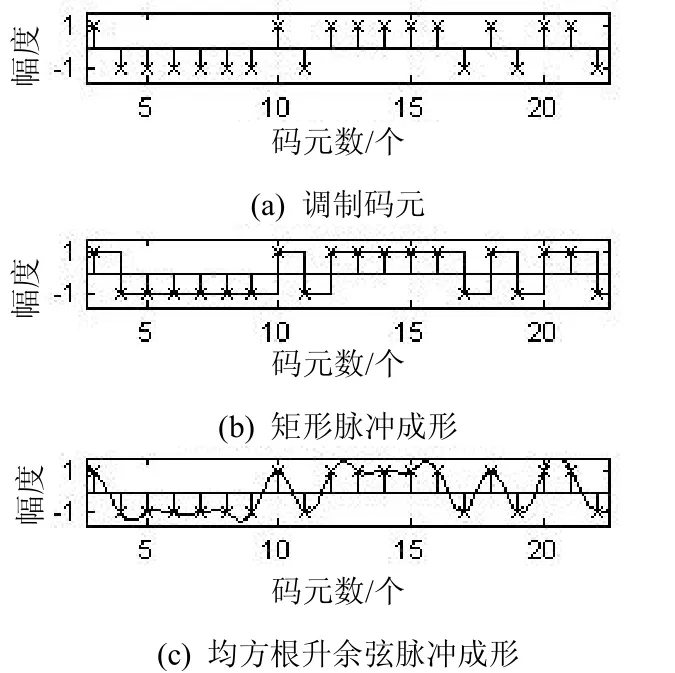
图1 成形基带信号

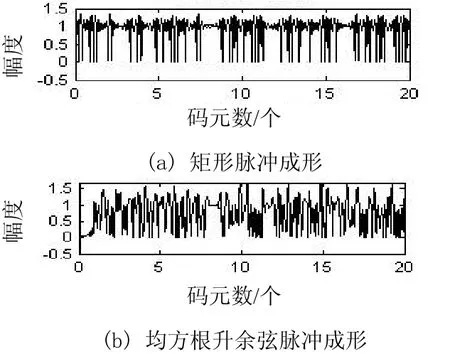
图2 成形信号瞬时幅度

2 信号的谱线特征分析

S(t)的n次方谱为[3]：

式中， {}F⋅为傅里叶变换。

对于BPSK信号，其表达式为：

二次方谱为：

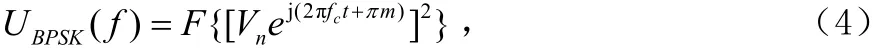
因 0,1m= ，故有：

可得：

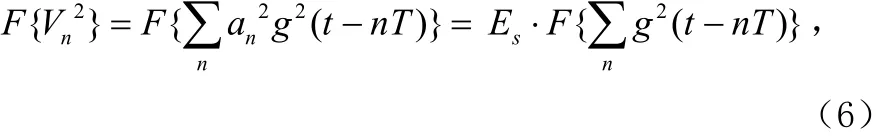
式中，sE为符号能量。因2( )gtnT- 是周期函数，故有：

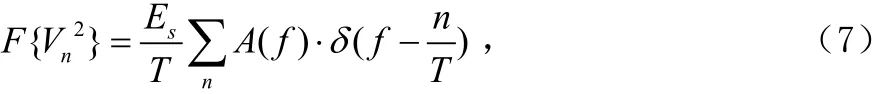
式中， A (f ) = G (f ) ∗ G (f )，G(f ) = F {g(t)}。 G (f)的衰减使F{}只在 f = { 0,±1 /T }处出现谱线,故(f)只在f = { 2 fc, 2 fc± 1 /T}处出现谱线。其他信号的谱线特征也可类似得到，如图3、图4所示。

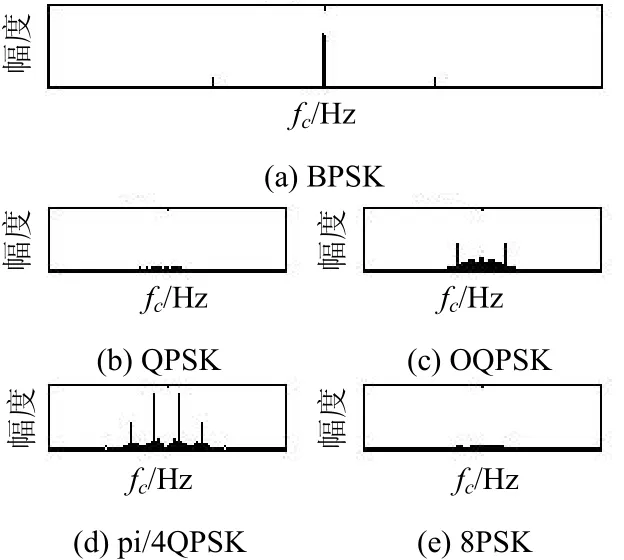
图3 二次谱线

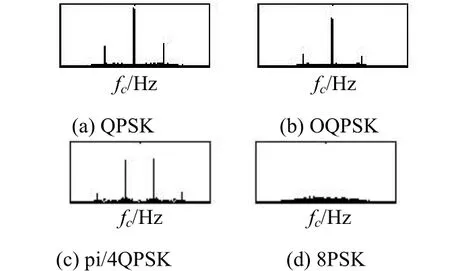
图4 四次谱线

3 信号谱线特征参数提取

由图4和图5可知，复信号谱线具有对称性，二次谱线对称轴为二倍载频，四次谱线对称轴为四倍载频。根据对称性，提出如下参数：

LVn：判断离散谱线是否存在。图3和图4中，有部分信号的谱线是不存在的，如QPSK的二次谱线。对吴月娴等[4]提出的参数进行改进，提出n次方谱离散谱线检测参数：

式中，N表示 U (f)的长度， Pn表示信号功率， Fs表示取样频率。当 L Vn大于某一门限值α时，认为离散谱线存在。

Fn：判断谱线图是平坦还是多峰。范海波等[5]提出了平坦指数来进行分析，但是需要对信号的载波频率进行估算。现进行改进：

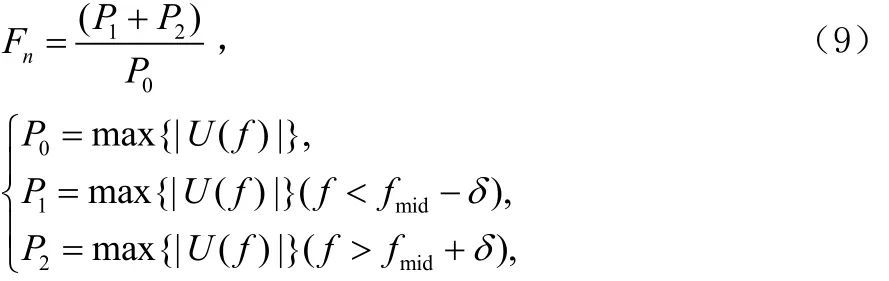
式中， fmid为max{|U(f ) |}对应的频率，N为 U (f)的长度，δ可减小 fmid邻近频率处|U(f)|的影响。当 Fn＜＜2时，认为谱线在 fmid处有一谱线存在；当 Fn＞＞2时，认为谱线在 fmid处无谱线存在。

设计识别流程为：对信号进行预处理；根据 F2，识别出BPSK；根据 L V4和 F2，识别出8PSK和QPSK；根据 L V2和F4，识别出pi/4QPSK和OQPSK。

4 实验仿真分析

如图5(a)所示，QPSK与8PSK的4LV在不同信噪比下具有很好的区分能力；如图5(b)所示，OQPSK的4F值远小于pi/4QPSK的4F值，故4F有效；如图6所示，信噪比不低于8 dB时，信号的识别率均高于95%。

图5 nLV和 4F随信噪比的变化

图6 识别率随信噪比的变化

5 结语

研究了均方根升余弦脉冲成形对 PSK信号瞬时特性的影响，并对BPSK、QPSK、OQPSK、pi/4QPSK以及 8PSK等5种常见PSK信号的二次谱线特征和四次谱线特征进行了详细的推导与实验仿真。根据不同信号谱线特征的差异性，提出了两个新的特征参数对其进行了识别。仿真结果表明，提出的两个参数受信噪比的影响不大，在较低信噪比条件下，仍然有较高的识别率。同时特征参数的提取过程非常简单，对先验知识的依赖性很小，因此能够很好地满足实际工程的需要。

[1] Dobre O A, BDI A A, NESS Y B, et al. Survey of Automatic Modulation Classification Techniques： Classical Approaches and New Trends[J].IET Communications,2007,1(02)：137-156.

[2] 杨伟超,张忠,丁群.低信噪比数字通信信号识别算法研究[J].通信技术,2009,42(01)：68-70.

[3] 杨琳,许小东,路友荣,等.常见数字通信信号的谱线特征分析[J].电子与信息学报,2009,31(05)：1067-1071.

[4] 吴月娴,葛东临,许志勇.常见数字调制信号识别的一种新方法[J].电子学报,2007,35(04)：782-785.

[5] 范海波,杨志俊,曹志刚.卫星通信常用调制方式的自动识别[J].通信学报,2004,25(01)：140-149.